Enhancing On-demand Transportation: Prioritizing Travel Costs with Hybrid Evolutionary Algorithms
Sonia Nasri1*, Hend Bouziri2, Wassila Aggoune Mtalaa3
1LARODEC Laboratory, Business Higher School of Tunis, Manouba University, Tunisia
2LARODEC Laboratory, Higher School of Economics and Business, Tunis University, Tunisia
3Luxembourg Institute of Science and Technology, Esch-sur-Alzette, Luxembourg
*Correspondence to: Sonia Nasri, PhD, Professor, LARODEC Laboratory, Business Higher School, Manouba University, Tunis, 2010, Tunis Governorate, Tunisia; E-mail: sonia15.nasri@gmail.com
DOI: 10.53964/mit.2024001
Abstract
Objective: Enhancing sustainability in on-demand transportation is a challenging task by offering flexible and optimized mobility solutions. This study focuses on on-demand mobility systems. We introduce a novel evolutionary computing method designed to address a bi-objective customized on-demand transportation problem, aiming to minimize total travel cost and total waiting time.
Methods: The method incorporates specific optimization techniques, along with an efficient dominance sorting approach, using an intelligent candidate list to reduce computational time.
Results: Comparative results demonstrate the effectiveness of this hybrid computing method, particularly when prioritizing total travel cost from the service provider’s perspective.
Conclusion: These findings present a promising framework for decision-makers, empowering them to navigate favorable compromises between conflicting objectives and make informed choices aligned with their preferences and customer-oriented constraints.
Keywords: making decision systems, passenger transportation, quality of service, multi-objective methods, evolutionary algorithm
1 INTRODUCTION
On-demand transportation emerges as a significant challenge to sustainable development within an interactive design. Interactive design contributes in creating user interfaces for people transportation systems, see works by Dolgui et al[1]. This might involve developing customized mobile applications to facilitate persons movement between different zones or sites. By merging interactive design with persons transportation in cities, transportation system providers can enhance the passengers experience during their trips. This helps optimizing operational efficiency and deals with a more connected and interactive environment. Figure 1 illustrates an interactive design involving connection between customers preferences, vehicles availability and transportation network locations.
|
Figure 1. An illustrative example of an on-demand mobility system.
As in Figure 1, unlike fixed-route services with predetermined schedules, on-demand transportation operates based on specific requests or needs, deviating from the usual routes and timetables. Optimal routing plans are produced basing on a customized design involving the management of customers’ requests, vehicles routing, and scheduling time.
The corresponding class of transport problems was initially introduced by Cordeau and Laporte[2] to individuals with reduced mobility and called the dial-a-ride problem (DARP). This on-demand transportation mode has now expanded to serve a wide range of purposes. These include healthcare organizations, integrated transportation systems, complementary services, and private transportation needs. Consequently, there is a need to tackle the modelling of new characteristics associated with on-demand transportation, a task that presents significant challenges. Encouragement is given to the development of advanced designs that accommodate real-life scenarios and address the diverse needs of customers. For further insights into this field, refer to the survey conducted by Nasri et al.[3], where a new category of customer-oriented on-demand mobility was introduced.
This present work focuses on the customer oriented dial-a-ride problem (CODARP) introduced by Nasri et al[4]. The primary goal of this problem is the minimization of the overall travel costs while considering the negative impact of waiting times using appropriate penalties. The mathematical model incorporates customized constraints that are directly associated with the maximal riding time, which represents the maximum duration passengers spend aboard a vehicle, as well as time windows designated for specific locations. The significance of the CODARP extends to both the service provider and the customers, as it effectively reduces the total riding time and eliminates unnecessary waiting periods.
Another effective approach to simultaneously minimize the total travel costs (TTC) and maximize the quality of the service provided to the customer is to formulate the quantities as two objectives. Various researchers in the field have opted for bi- objective designs. Customer-oriented DARPs have been solved using multi-objective models[5]. The model proposed by Nasri et al.[5] is a bi-objective CODARP, minimizing two distinct objectives. The primary objective focused on minimizing total transport costs, while the secondary objective aimed to minimize total waiting times (TWT). The experimentation is conducted within CPLEX (IBM CPLEX high-performance optimization solvers) on real-world instances. Main results indicated that prioritizing the minimization of waiting times, as opposed to total costs, resulted in notable decreases in waiting times across the majority of cases.
In the field of multi-objective applications, the pareto ranking scheme has been frequently employed, as highlighted in the research of Ref[6] and Ref[7]. The Pareto ranking process aims to rank solutions and identify those that are non-dominated. While there are several Pareto ranking methods available to find non-dominated solutions, many of them are computationally intensive. The Pareto Front represents a set of solutions where no single solution can be improved in one objective without causing a detriment in another. Essentially, it embodies the optimal compromise solutions, showcasing the delicate balance required in addressing conflicting objectives. Complementing the pareto front is the approximation set, which comprises a subset of solutions that approximates the pareto front. This set encapsulates a diverse array of solutions that provides decision-makers with a comprehensive view of the trade-offs inherent in the optimization problem.
In our study, we refer to a non-dominated sorting procedure inspired from the hierarchical non-dominated sorting (HNDS) technique of Ref[6]. This advanced technique is an effective method for efficiently ranking solutions based on their dominance relationships. In this paper the bi-objective CODARP[5] is solved via a lexicographic optimization method involving a hierarchical ordering of objectives. The prioritization is performed using a lexicographic technique implemented by CPLEX. The assessment of the optimal fronts is based on a performance measure. The proposed evolutionary algorithm named evolutionary lexicographic algorithm2 (ELEXA) is guided by the prioritized order achieved by the lexicographic technique output. This algorithm relies on the hierarchical ranking procedure named HNDS to generate new populations with a faster and quick technique. A new perturbation and a crossover operator are implemented to provide good distributions of the trade-offs in the solutions space.
These operators are tailored for supporting the customized design of the problem under consideration. The set of approximate solutions selected by our evolutionary method are comparable to the ones provided by CPLEX. The results of ELEXA are also competitive as compared with the methods of the literature.
The structure of this study follows this order: A literature review is presented in section 2. Section 3 aims at defining the bi-objective Customer-Oriented problem. In section 4, the Evolutionary Lexicographic Algorithm is presented. The next section 5 presents an experimental study of the problem. Finally, a conclusion is reported in the last section 6.
2 RELATED WORKS
Recent advancements in on-demand transportation technologies[5,7-9] have led to significant innovations. These emerging technologies incorporate designs tailored to customer preferences[3], offering customization in the transportation of persons. These systems rely on customized mobile applications, enabling persons to plan their journeys based on specific needs, whether it’s moving between different zones or accessing multiple sites within a region.
Furthermore, these technologies incorporate inter- active elements on board vehicles, providing personalized trips. These advancements would significantly contribute in how people transportation is conceived and implemented within transportation systems, with increased emphasis on user experience, operational efficiency, and passengers’ satisfaction.
Bi-objective on-demand problems[10,11] with customized service quality design have received significant attention in transportation research. These problems aim to optimize vehicle routing plans while considering multiple objectives and meeting specific quality-of-service criteria.
Molenbruch et al.[11] investigated a patient transport system and proposed a bi-objective model for minimizing the total travel distance, while also considering the balance between operational costs and service quality. This trade-off was captured by an additional objective, aiming to minimize the overall ride time for users. Through real-life simulations, the study assessed the resulting costs for the service providers, while ensuring compliance with constraints such as the time windows ones and the maximum ride time.
Hybridized evolutionary methods are of growing interest for the researchers, see the existing related works[12-16]. Chassaing et al.[12] proposed a hybridized evolutionary algorithm combined with a local search-based method managing optimization techniques within dynamic probabilities for solving DARPs using a customized maximal ride time. Artificial instances[17] were enriched with special real-world features to better reflect the service providers requirements. A multi-objective dial-a-ride model aimed to optimize various objectives such as costs and user inconvenience[8]. The optimization process takes into account the vehicles and passengers’ constraints, including factors like their capacity and the time windows. To solve this problem effectively, three multi-objective evolutionary algorithms are employed. Moreover, Ren et al.[14] proposed a multi-objective optimization formulation of a transportation system, taking into account the preference ranks of requests for multiple boarding stops. The main goals of the model are the minimization of the travel costs and the number of unsatisfied requests, which serves as an indicator of the quality of service. To tackle this problem, a hybridized solution method is developed, combining a variable neighborhood search technique with a quick elitist non- dominated sorting genetic algorithm. The use of multi-objective optimization methods and hybrid evolutionary algorithms demonstrated promising results in improving the overall service quality and efficiency of dial-a-ride systems. Further research is needed to explore new algorithms, optimization models, and decision-making frameworks to address the complexities of this problem domain and meet the evolving needs of transportation ser- vices in real-life scenarios. In this regard, we are interested in exploring real-life resolutions that take into account customer issues. In our opinion, models addressing both the interest of the customer and the service provider under advanced quality specifications deserve new tailored evolutionary algorithms. This is what motivates this present study.
Furthermore, current approaches, though some- what effective, encounter with issues like inefficient resource allocation, long wait times, and difficulty adapting to customized changing demand. These challenges highlight the need for new solutions that can overcome these problems and simultaneously optimize multiple, sometimes conflicting, goals. The shortcomings in current algorithms become particularly evident when dealing with the complexities of real-world on-demand mobility scenarios. Factors like user preferences require a more adaptable decision-making process.
By using multi-objective optimization methods and hybrid evolutionary algorithms, our goal is not only to address the inefficiencies in cur- rent systems but also to establish a more robust and responsive foundation for on-demand mobility system operations. We aim to contribute to the advancement of intelligent transportation systems, improving the overall quality and efficiency.
3 THE BI-OBJECTIVE CUSTOMER-ORIENTED DARP
The bi-objective CODARP[5] involves the transportation of passengers with specific transportation demands. In the bi-objective CODARP, two objectives are considered seeking for optimizing the routing plans for vehicles while considering the requests, schedules, and vehicles constraints. The two objectives are the TTC and the TWT.
All the customers, who require transportation from an origin location to a destination, have their own maximum riding time, which represents the acceptable duration they are willing to spend aboard a vehicle. This maximum riding time is used to calculate new time windows based on specific customer’s parameters, thereby enhancing the quality of service.
A transportation request may involve multiple passengers, and a homogeneous fleet of dedicated vehicles is responsible for transporting these passengers. The vehicles start and end their routes at the depot. Each request in the problem corresponds to a pickup node i, where i belongs to the set {1...n}, and a delivery node j, where j belongs to the set {i+1...2n}. Here, n represents the total number of requests. Specifically, a request consists of a pickup node i and a corresponding delivery node i+n. The number of requests is equivalent to the number of pickups. The depot is represented by two nodes, namely 0 and 2n +1. The problem’s parameters are presented in Table 1.
Table 1. The Problem’s Parameters
Parameters |
Definitions |
N |
Set of nodes, which includes the pickup and delivery sites. |
v |
Index representing a specific vehicle. |
m |
Total number of vehicles. |
ti |
Service time required at |
Biv |
Beginning of service at node i. |
Ariv |
Arrival time at node i |
Wiv |
Waiting time of vehicle v at node i. |
The objective of this problem is the minimization of both the TTC, as defined in Equation (1), and the TWT, as presented in Equation (2), The TTC represents the operational costs associated with the routing of the available vehicles to fulfil a given number of requests. These operational costs are the sum of the routing costs of the arcs (i, j) that the vehicles traverse. The cost of an arc (i, j) is determined by the sum of the transit time on the visited arc and the service duration at the origin node, denoted as c(i, j).
|
In Equation (3), we present the expression of the waiting time Wiv computation, being the difference between the beginning of service Biv and the arrival time Ariv at node i.
|
4 THE HYBRID EVOLUTIONARY LEXICOGRAPHIC METHOD
This section is devoted to the presentation of the components of the hybrid evolutionary lexicographic method. In this method, we investigate a construction heuristic for the initial solution, a perturbation operator for constructing the population, and a crossover operator. These techniques are specially dedicated to adequately supporting the real-life nature of the problem.
Moreover, the ELEXA relies on a prioritized objective function which is provided by a lexicographic technique described in subsection 5.2. This priority enables the ELEXA to select the best solution and helps in the ranking process. This method performs a sorting routine on the offspring to generate the set of non-dominated solutions based on the prioritized objective function. These offspring solutions are ranked using the HNDS algorithm. The HDNS algorithm is based on eliminating unnecessary dominance comparisons. This ranking procedure sorts the solutions using the first objective. Then, the procedure calculates an order for each temporary sorted solution according to the second objective saving many comparisons and reducing the run time. In fact, it consists in discarding the dominated solutions of the first resulted rank and thus reducing the number of comparisons. The advantage of this technique is its speed to select at each step of comparison a non-dominated individual. Therefore, the HNDS approach is well suited since it is also based on the lexicographic ordering of the priorities given to the two objectives.
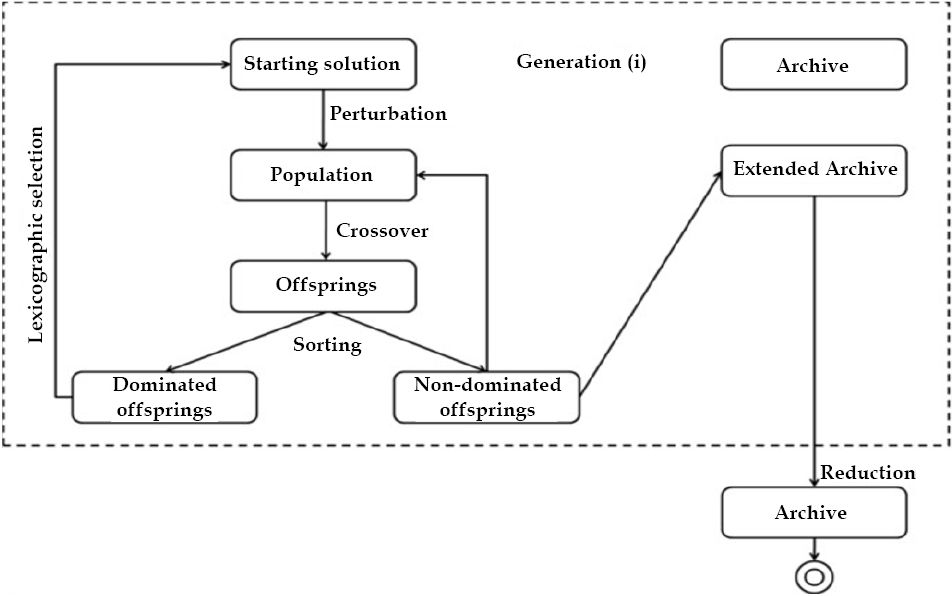
As described in Figure 2, the ELEXA relies on an archive saving non-dominated solutions provided at each generation. The set of variables used in the algorithm are indicated in Table 2.
|
Figure 2. An overview of the ELEXA.
Table 2. The Algorithm’s Parameters
Parameters |
Definitions |
max |
Maximal number of iterations. |
np |
Total number of individuals. |
P |
Population. |
init |
Initial solution. |
pr |
Priority of the objective function. |
A |
Extended archive set. |
H |
Set of non-dominated solutions. |
T |
Set of non-dominated solutions. |
The algorithm returns the archive reduced by applying the sorting method to preserve only the Pareto front. The method applies an elitism by incorporating the current non-dominated offspring in the new population, which is completed by the selected dominated solution and its perturbed individuals.
To generate the population, an initial solution is constructed by the mean of the insertion heuristic (see subsection 4.1). This initial solution is then perturbed by the mean of a perturbation operator (see subsection 2) producing np individuals (lines 10-14). Then a crossover operator (see subsection 4.3) is applied to each individual (line 16). These offsprings are sorted and ranked using the HNDS algorithm. The individuals of the Pareto front are then archived. These latter are added to the extended archive (line 19). As the non-dominated solutions are separated from the dominated ones, they are saved in two sets namely H and T respectively. The non-dominated solutions are added to the extended archive and incorporated in the new population (line 9) for the next generation. Steps are provided in Algorithm 1. (Table 3)
Table 3. Algorithm 1 The Evolutionary Lexicographic Algorithm
1: Input max, np |
2: Output Best set |
3: init ← insertion heuristic() |
4: nb indiv ← 0 |
5: pr ← pr TTC |
6: A ← ∅ |
7: H ← ∅ |
8: for (nb iter = 1) do max iter |
9: P ← H |
10: repeat |
11: indiv ← perturbation(init) |
12: Add(P, indiv) |
13: nb indiv ← nb indiv + 1 |
14: until nb indiv = np − |H| |
15: for (all indiv ∈ P) do |
16: crossover(indiv) |
17: end for |
18: H ← HNDS(P) |
19: A ← A ∪ H |
20: T ← P \ H |
21: init ← select best(T, pr) |
22: Exchange priority(pr) |
23: end for |
24: Best set ← HNDS(A) |
Furthermore, a best solution is selected from the dominated solutions saved in T (line 21).
selection involves the evaluation of the solutions according to the current priority. The best one is used for the next iteration in the evolutionary algorithm. Consequently, the new population of the next generation consists of the resulted non-dominated solutions in the set H and new individuals produced by perturbation. With this regard, ELEXA benefits from elitism technique of the HDNS. However, before iterating, the priority is exchanged assuming another lexicographic order for the evolutionary search. When the maximum number of generations (max) is reached, the algorithm keeps the ranked set of solutions from the reduced archive obtained by applying the HNDS sorting algorithm.
4.1 The Construction of the Initial Solution
In order to create the initial solution, we refer to the heuristic method as described in Ref[4]. This insertion heuristic initially organizes the requests in an ascending order based on their earliest ser- vice times. It then selects an appropriate vehicle by considering factors such as its capacity and total duration, ensuring its availability for the task. The requests are placed into the tours of the vehicles, ensuring the fulfilment of all constraints and adherence to the designated time schedules. If a request is successfully assigned to a vehicle, the relevant parameters associated with the vehicles, requests, and time schedules are appropriately updated.
To free up some capacity in the vehicles, the deliveries with the earliest service times are ensured, and all the corresponding updates are made. This process is also executed when some violations of the maximum riding time occur during the insertion of a new request into the tour. Addition- ally, a vehicle is marked as non-available once its maximum total tour duration is reached. Finally, the process continues until all the requests are satisfied.
4.2 The Population Generation in ELEXA
To generate the population, a new perturbation operator is proposed. The operator selects a request with a waiting time which occurs either at the pickup or the delivery node, and then moves this request to another route. This operation involves the computation of time windows, which results in a new beginning of service. Algorithm 2 presents the main steps of the perturbation. (Table 4)
Table 4. Algorithm 2 the Perturbation Procedure
Algorithm 2 |
1: Given a solution S; |
2: Save in a list L the set of requests having waiting times; |
3: Save in a list R the set of requests without waiting time ; |
4: if L is not empty then |
5: Select a request r from L; |
6: Compute customized time windows for r; |
7: else |
8: Select a random request r from R; |
9: end if |
10: Seek for a new position in another route; |
11: Move the request r to the new route; |
12: Update the time schedule in S; |
13: Return obtained solution; |
The procedure starts by separating requests into two distinct lists (lines 2 and 3): L, which stores requests associated with waiting times, and R, which contains requests without waiting times. Next, it evaluates whether the list L contains any requests with waiting times. If the list is not empty, the procedure selects a request from L and computes customized time windows at line 6 for that particular request. In cases where L is empty, the algorithm randomly selects a request from list R at line 8. Following the selection process, it seeks an optimal position (line 10) within another route to accommodate the chosen request. Upon identifying a suitable position, the procedure relocates the request to this new route and proceeds to update the time schedule (line 12) within the solution S accordingly. The final step involves returning the new solution obtained through the application of this perturbation procedure.
4.3 The Generation of Offsprings
The offspring solutions are created basing on the crossover procedure which is inspired from the one provided in Ref[4]. It enables the offspring solution to inherit the beneficial characteristics from both parents, particularly the high level of quality of service achieved during the previous perturbation phase. During the crossover process, two selected routes originating from the same individual act as parents. This process involves identifying two positions on the two routes that correspond to the first pickup nodes with similar or closely aligned starting service times. Next, the procedure removes the sequences of requests from the routes that fall out- side the designated cut points in each parent. The exchange of the two resulting sections in the two routes is performed while maintaining the same positions in the time schedule. Finally, in the final phase, the recombination proceeds by inserting the deleted requests into the resulting solution, aiming to retain their original positions in the parent while ensuring the problem’s constraints.
5 EXPERIMENTAL STUDY
To demonstrate the effectiveness of the ELEXA, we conduct a comparative analysis involving preliminary experimentation. Thus, we use CPLEX, a widely used mathematical solver, to obtain optimal fronts when varying the priority. This part of the study is important since it demonstrates the behavior of the solutions within two hierarchical lexicographic orders.
To assess the optimal fronts and fix the suitable lexicographic order for the ELEXA, we refer to the C-metric performance tool[18]. This performance metric determines the proportion of solutions of in a preliminary defined approximation set which are dominated by or equal to the solutions in a competing approximation set.
The resulting outputs of ELEXA are then com- pared with the results obtained with of methods from the literature. In this regard, we are able to highlight which output of each method is meaningful when addressing the interest of the customer and the transport service provider.
5.1 The Dataset Used for the Experimentation
Real-life cases of transport on-demand, proposed by Ref[19], are employed for conducting tests. These instances reflect realistic scenarios, where the locations are based on the GPS positions of the nodes and the actual distances between them. The transportation network density varies across different instances, and so does the distribution of the customers over the space. These instances are designed for real-life situations and specific condi- tions. The distances between the pickup and destination points for the customers are distributed, with the majority of the transportation requests (75%) representing a distance of between 30km and 70km. The time windows depend on both the pickup and destination locations. The size of these time windows varies depending on the specific customer. The maximum riding time and the travel distance of the request is an individual requirement of each customer. The number of customers at a site can range from 1 to 4. All the vehicles have an average speed of 1.33 km per minute. The maximum duration for a vehicle’s tour is set at 480 min, and the vehicles can only carry 8 passengers at a time. The lexicographic objective function order
The lexicographic method was introduced by Dolgui et al[1]. It is a non-scalar approach used to handle multiple objectives in decision-making. This method organizes the objectives based on a specified priority order determined by the decision-maker. It establishes a ranked list of objectives, sorted in the decreasing order of their importance. When solving a problem using the lexicographic method, each objective is optimized one at a time, starting from the highest-priority objective and proceeding to lower-priority objectives. The method ensures that once an optimal solution is found for an objective, only solutions that are also optimal for the higher-priority objectives are considered for the remaining objectives. This hierarchical approach guarantees that the resulting solution adheres to the desired priority order.
This lexicographic technique is implemented in the CPLEX tool. We explore two variations of the lexicographic method: LexTTC and Lex- TWT. The LexTTC version prioritizes the TTC as the first objective, while the Lex- TWT version gives priority to the TWT. Experiments are conducted using 10 On-Demand Transport problems. These problem instances were solved using the CPLEX software with a computation duration of maximum two hours.
In order to well assess the produced solutions in the Pareto front, we use a performance measure. The C-metric assigns a value within the range [0, 1] to the ordered pair (A, B) and is defined by Equation (4).
|
If the value of C(A, B) is 1, it indicates that all the solutions in the set B are either dominated by or equal to the solutions in the set A. Conversely, if C(A, B) is 0, all the solutions in B strictly dominate the solutions in the set A. It is thus important to compute both orderings in this context.
Table 5 presents the coverage of the two sets of solutions obtained with LexTTC and LexTWT. It provides an overview of the problem instances, including their names, the number of requests (n), and the number of vehicles (m) involved. Let A and B represent two approximations of the Pareto set. Let us consider A as the set of solutions of LexTTC and B as the set of solutions of LexTWT.
Table 5. The Coverage of the Approximate Sets
Instances |
n |
m |
C(A,B) |
C(B,A) |
Coverage |
d75 |
10 |
2 |
0.33 |
0 |
A strictly dominates B |
d92 |
17 |
2 |
0.30 |
0.83 |
No coverage |
d93 |
20 |
2 |
0 |
0.66 |
B strictly dominates A |
d94 |
23 |
2 |
0.25 |
0.14 |
No coverage |
d55 |
28 |
4 |
0.43 |
0 |
A strictly dominates B |
d52 |
29 |
4 |
0.28 |
0 |
A strictly dominates B |
d10 |
34 |
4 |
0.25 |
0.14 |
No coverage |
d39 |
38 |
6 |
0.6 |
0 |
A strictly dominates B |
d70 |
39 |
6 |
0 |
0.5 |
B strictly dominates A |
d82 |
39 |
6 |
0.6 |
0 |
A strictly dominates B |
According to Table 5, prioritizing the TTC within the LexTTC method yields superior compromises between the service provider’s and the customer’s interests. Specifically, there are five cases where C(B, A) equals zero, indicating minimal travel costs, while there are only two cases where C(A, B) equals zero when the waiting time is prioritized. This demonstrates that prioritizing TTC leads to solutions with a high level of quality of service, even if the TTC is emphasized. The lexicographic resolution of the bi-objective model shows promising solutions. When the TWT is prioritized, it yields the best outcomes from the customer’s perspective. However, preliminary experiments suggest that prioritizing the TTC leads to better compromises between the travel costs and the waiting times.
5.2 Comparison Between ELEXA and LexTTC
The lexicographic resolution of the bi-objective problem demonstrated its combinatorial nature, as evidenced by the extensive computational time required for the exact method executed by CPLEX on the previously analyzed instances, ranging from one to two hours. This computational complexity served as a motivation for us to develop a metaheuristic method capable of quickly generating solutions of reasonable quality. In this regard, we opt for an evolutionary method, which is widely recognized for its effectiveness in addressing multi-objective optimization problems. Hence, we will focus on testing this method exclusively on the instances that were previously analyzed using the lexicographic exact resolution discussed previously.
Given the dominance of the results produced by the exact resolution when the TTC is prioritized, this objective function is used as an evaluation criterion for the ELEXA. The obtained results are assessed when comparing with optimal fronts of the LexTTC resolution.
To perform experiments using the evolutionary algorithm, two parameters are considered: the population size and the maximal number of iterations. These parameters were determined through preliminary tests. Thus, we set the population size to 100 and ran the evolutionary algorithm, named ELEXA, for 1000 iterations.
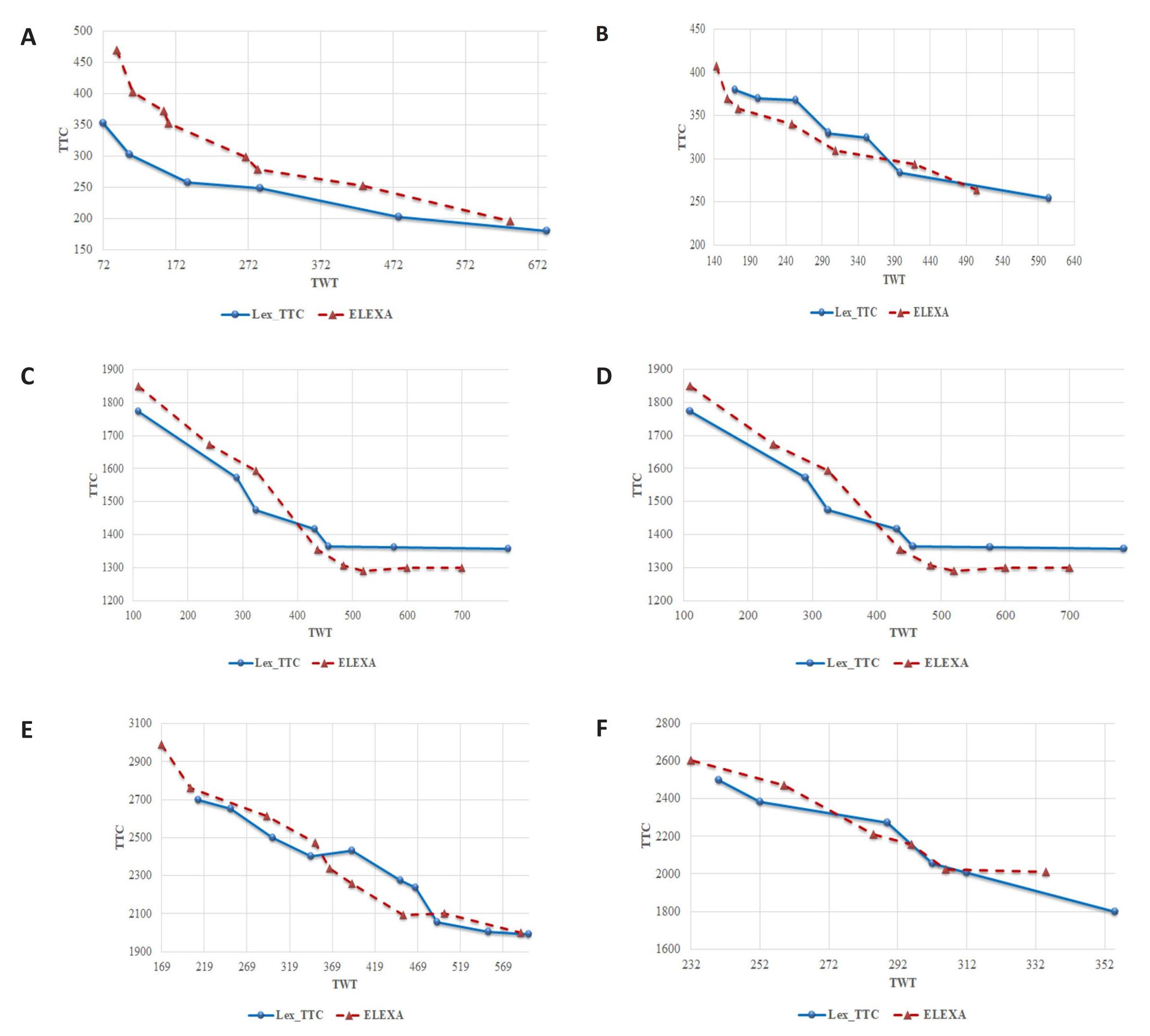
Figure 3 displays Pareto fronts obtained by the ELEXA within some problems’ instances. These fronts are compared with the optimal solutions generated by the exact method LexTTC solved with CPLEX.
|
Figure 3. Pareto fronts obtained for the (A) d92, (B) d93, (C) d94, (D) d10, (E) d70, and (E) d82 instance.
According to results observed in Figure 3, ELEXA yields promising results when compared to the exact solution provided by LexTTC. The solutions obtained by ELEXA show a good performance in terms of trade-offs between the objectives.
For instances with a larger number of requests (n>30). ELEXA outperforms LexTTC by generating solutions that are closer to the optimal ones. Additionally, ELEXA demonstrates its effective- ness in providing competitive solutions, which is consistent with the coverage observed in LexTTC (refer to Table 2 in section 3). This behavior is particularly notable for the d10 instance, where no coverage is found between LexTTC and LexTWT. The ELEXA provides a greater diversity of well- distributed solutions on its Pareto fronts com- pared to the exact method LexTTC as for the instances d75 and d55. Moreover, for the case of d93 in Figure 3B, a significant majority of the solutions generated by ELEXA dominate those of LexTTC. This improvement in solution quality is especially marked in cases where the coverage is observed in LexTWT. The performance of the ELEXA can be attributed to two key factors which are the incorporation of elitism, dominance rules in the algorithm design, its customized operators and the rapid convergence of ELEXA to Pareto fronts.
Table 6 reports the CPU (Central Processing Unit) times per minutes (m) required to solve the problem using the ELEXA and the LexTTC methods.
Table 6. Computational Times
Instances |
LexTTC CPU(min) |
ELEXA CPU(min) |
d75 |
35.22 |
7.28 |
d92 |
40.37 |
11.43 |
d93 |
55.12 |
15,20 |
d94 |
66.53 |
15.21 |
d55 |
70.23 |
17.66 |
d52 |
86.14 |
18.08 |
d10 |
91.33 |
18.14 |
d39 |
104.47 |
18.62 |
d70 |
113.52 |
19.04 |
d82 |
118.17 |
19.78 |
As shown in Table 6, ELEXA proves to be significantly faster than the exact method named LexTTC. The results highlight that ELEXA requires considerably less time, with execution times ranging up to 20 minutes, in comparison to CPLEX, which can take up to 2 hours. Table 6 illustrates that the ELEXA reduces the execution time by at least one hour.
With a large number of requests (n>30). This reduced time requirement allows ELEXA to con- verge rapidly, resulting in better Pareto fronts in terms of both diversity and convergence.
5.3 Comparative Study Between ELEXA and A State-of-the-Art Method
To well assess the behavior of our approach when addressing the bi-objective CODARP, a comparison is performed regarding another mono-objective method applied for the same trans- port on-demand problems. The mono-objective approach is named evolutionary local search (ELS) of Ref[12]. In this method, the objective is to minimize the TTC. To be able to compare between the results of the mono-objective method named ELS and ELEXA, the extreme solutions in the Pareto optimal set provided by the ELEXA are first calculated. An extreme solution corresponds to the best solution found for each objective function. Thus, for each instance, we have performed a total of 10 executions for the ELEXA run for 1000 iterations. From this total of 10 values, we calculated the mean of the best objective values for the TTC and the TWT. In order to provide a deeper analysis of the results, further problems are selected from the data set of instances of Chassaing [19]. Instances with a total number of requests up to 60 are provided for a comparison with the state-of-the-art method. The results shown in Table 7 report for each instance, the values (minutesof TTC and TWT related to ELS, and ELEXA successively. Besides, Gaps between values are also reported in the table. Negative gaps (%) indicate improved values either in TTC or TWT.
Table 7. Obtained Results in ELS vs. ELEXA
Instances |
m |
n |
TTC(min) |
GAPTTC (%) |
TWT(min) |
GAPTWT (%) |
||
ELS |
ELEXA |
ELS |
ELEXA |
|||||
d75 |
2 |
10 |
150.91 |
144.47 |
-4.26 |
398.54 |
345.11 |
-13.41 |
d92 |
2 |
17 |
347.01 |
337.46 |
-2.75 |
250.08 |
215.05 |
-14.01 |
d93 |
3 |
20 |
418.76 |
411.51 |
-1.73 |
177.34 |
180.13 |
1.57 |
d94 |
2 |
23 |
352.25 |
345.01 |
-2.05 |
153.79 |
163.22 |
6.13 |
d55 |
5 |
28 |
1,516.71 |
1529.15 |
0.82 |
202.63 |
165.54 |
-18.30 |
d52 |
4 |
29 |
1,607.74 |
1,601.36 |
-0.40 |
70.81 |
60.42 |
-14.67 |
d10 |
4 |
34 |
1,341.02 |
1,400.75 |
4.45 |
377.87 |
344.15 |
-8.92 |
d39 |
6 |
38 |
2,030.44 |
2,000.23 |
-1.49 |
524.72 |
399.33 |
-23.90 |
d70 |
6 |
39 |
2,006.05 |
2,005.40 |
-0.03 |
144.29 |
149.44 |
3.57 |
d82 |
6 |
39 |
1,842.84 |
1,866.01 |
1.26 |
95.27 |
99.75 |
4.70 |
d08 |
7 |
42 |
1,857.35 |
1,791.42 |
-3.55 |
482.47 |
423.52 |
-12.22 |
d36 |
6 |
42 |
2,139.52 |
2,134.90 |
-0.22 |
390.74 |
299.24 |
-23.42 |
d43 |
6 |
43 |
2,002.15 |
1,992.16 |
-0.50 |
189.57 |
203.43 |
7.31 |
d01 |
7 |
46 |
2,396.55 |
2,294.11 |
-4.27 |
212.50 |
229.41 |
7.96 |
d11 |
7 |
47 |
2,538.18 |
2,433.55 |
-4.12 |
141.18 |
122.12 |
-13.50 |
d90 |
6 |
51 |
1,133.45 |
1,155.87 |
1.98 |
355.15 |
351.66 |
-0.98 |
d17 |
8 |
52 |
2,861.93 |
2,986.76 |
4.36 |
234.73 |
256.74 |
9.38 |
d84 |
8 |
52 |
2,368.34 |
2,477.01 |
4.59 |
312.03 |
271.13 |
-13.11 |
d81 |
7 |
53 |
2,456.13 |
2,358.38 |
-3.98 |
333.38 |
291.45 |
-12.58 |
d96 |
11 |
53 |
3,593.60 |
3,503.11 |
-2.52 |
279.91 |
306.23 |
9.40 |
d07 |
8 |
54 |
3,082.80 |
3,102.23 |
0.63 |
167.80 |
174.33 |
3.89 |
d87 |
8 |
54 |
2,714.31 |
2,800.18 |
3.16 |
339.88 |
310.46 |
-8.66 |
d47 |
7 |
55 |
2,636.07 |
2,599.00 |
-1.41 |
301.51 |
325.55 |
7.97 |
d48 |
8 |
55 |
3,083.19 |
3,120.46 |
1.21 |
418.27 |
377.42 |
-9.77 |
d61 |
8 |
55 |
2,855.09 |
2,896.64 |
1.46 |
342.11 |
358.36 |
4.75 |
d12 |
9 |
56 |
3,614.27 |
3,527.89 |
-2.39 |
341.82 |
365.12 |
6.82 |
d20 |
9 |
56 |
3,567.32 |
3,633.05 |
1.84 |
394.84 |
371.63 |
-5.88 |
d30 |
8 |
56 |
2,678.58 |
2,800.63 |
4.56 |
286.48 |
241.44 |
-15.72 |
d53 |
7 |
57 |
2,484.60 |
2,391.08 |
-3.76 |
104.83 |
114.42 |
9.15 |
d05 |
9 |
58 |
3,393.09 |
3,420.12 |
0.80 |
400.98 |
319.11 |
-20.42 |
d13 |
9 |
59 |
3,183.19 |
3,200.20 |
0.53 |
441.76 |
368.34 |
-16.62 |
d06 |
10 |
60 |
3,412.34 |
3,444.12 |
0.93 |
523.99 |
414.09 |
-20.97 |
Regarding results of TTC and TWT in Table 7, the ELEXA indicates competitive results when comparing with ELS. Good enhancements are marked in term of TTC and TWT. Even for the cases which are not improved by ELEXA, the positive gaps are up to %5 in TTC. As we observe in TWT, the positive gap between values in ELS and ELEXA is up to 10% relating to the solutions where ELS is better than ELEXA. However, the negative gaps indicating improved values of TWT in ELEXA are up to 24%. This output emphasizes the contribution of the customized design in the bi-objective problem even when TTC is prioritized.
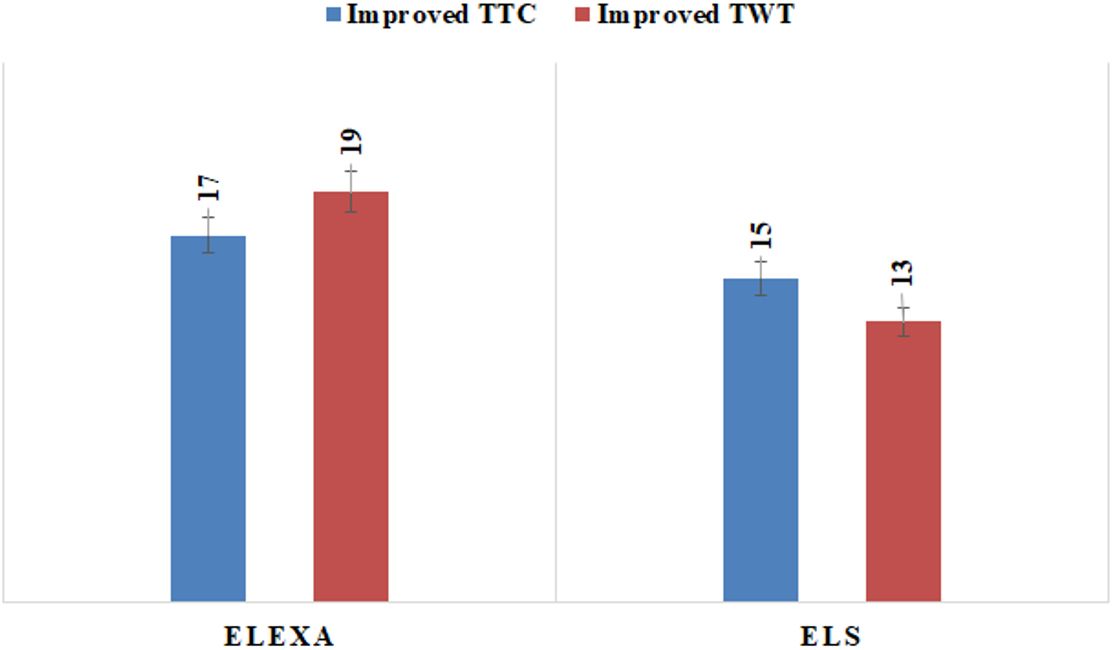
Furthermore, we deduce that globally ELEXA outperforms ELS. In Figure 4, the total number of improved cases in term of TTC and TWT is depicted for each method. In fact, in term of TTC, 17 improved cases are produced by ELEXA regarding 15 cases out of 32. However, ELEXA is more effective in term of TWT for 19 instances as compared with 13 solutions in ELS. This output indicates that ELEXA is able to provide good tradeoffs between TTC and TWT for decision making systems. Despite the mono-objective nature of ELS minimizing TTC, the results demonstrate that mono-objective approach may excel in this specific objective, but they might not achieve the same level of balance when handling multiple objectives simultaneously.
|
Figure 4. Total number of improved results produced by ELEXA and ELS.
When observing cases where ELEXA outperforms the mono-objective method, we emphasize 7 good compromises between TTC and TWT as for problems d75, d92, d52, d39, d36, d11, d81. These solutions are produced by ELEXA where both TTC and TWT are improved as compared by ELS. This leads us to deduce that the bi-objective method might be more interested when seeking good solutions satisfying both the service provider and customers. These findings offer valuable insights for decision-makers in demand-responsive passenger transportation. While the mono-objective method ELS is useful, the advantages and overall quality of solutions provided by ELEXA might be more relevant in contexts where simultaneously optimizing multiple objectives is crucial for user satisfaction and operational efficiency. Addressing the problem within ELEXA is promising by the use of the prioritized lexicographic order for TTC and the elitism process provided by the incorporation of the HDNS algorithm. The ELEXA’s effective- ness in managing multiple objectives simultaneously highlights its potential for decision-making in real-world transport scenarios. Moreover, the instances’ characteristics seem to influence the relative performance of each method. This variance in performance emphasizes the importance of adaptive algorithms when dealing with diverse real-world transportation scenarios.
Additionally, exploring hybrid approaches that combine strengths from both mono and bi- objective methods might offer a promising direction for future optimization techniques. The application of bi-objective optimization techniques like ELEXA prioritizing Travel cost can offer good trade-offs between different objectives, empower decision-makers to tailor transportation solutions that align more closely with users’ preferences and needs.
6 CONCLUSIONS
This paper addresses a customer-oriented trans- port on-demand problem using a bi-objective customized design. In this problem, TWT and TTC are considered as separate objectives. A lexicographic exact resolution is applied to determine an appropriate priority ordering for these two criteria with the aim of finding high-quality solutions. To address more real life on-demand transport problems, the study proposes a bi-objective optimization method based on an ELEXA. It incorporates optimization techniques tailored for supporting advanced designs of transportation services and an effective dominance sorting method to generate new populations of solutions with a faster and effective technique. Experimental results demonstrate that ELEXA reaches a promising performance on realistic on- demand instances while maintaining reasonable CPU time requirements. Future experiments could be conducted on a broader range of on demand transport problems, and the algorithm could be compared with other well-known multi-objective optimization methods. Future research could focus on enhancing ELEXA by incorporating adaptive mechanisms or hybridization with other meta- heuristic techniques. These improvements might aim to better handle diverse transportation scenarios, considering varying passenger demands and route complexities.
Furthermore, future works should extend the application of bi-objective optimization approaches to multi-modal transportation systems. This could involve optimizing passenger transportation across various modes. Besides, it is interesting to conduct extensive experimental validations using diverse data sets and benchmark problems derived from real-world transportation scenarios. Comparative studies with newly developed algorithms or modified versions could provide deeper insights into their relative performance and robustness. Additionally, the application of bi-objective optimization approaches to multi-modal transportation systems holds promise for logistics across different production units or plants. This approach could yield substantial benefits in terms of resource optimization and operational efficiency. To conclude, future studies in on- demand transportation systems should prioritize rigorous experimental validations using diverse data sets and real-world benchmark problems. Comparative analyses against other optimization methods or newly developed algorithms would offer valuable insights into the applicability, performance, and adaptability of these approaches.
Acknowledgements
We would like to express our sincere gratitude to Manouba University for providing the resources and support necessary for conducting this research. Special thanks to Pr. Hend Bouziri and Dr. Wassila Aggoune for their invaluable guidance, mentorship, and unwavering support throughout the duration of this study. Their expertise and insights have been instrumental in shaping the direction of our research and ensuring its successful completion. We are also thankful to the members of the LARODEC Laboratory at Tunis University for their collaboration and assistance, which greatly contributed to the execution of this project. This work was made possible by the collaborative efforts and dedication of everyone involved, and we are deeply appreciative of their contributions.
Author Contribution
Nasri S was responsible for conceptualizing the study, developing methodologies, managing software, conducting validation and formal analysis, curating data, writing the oringinal draft, and creating visual elements. Bouziri H was responsible for validating the study’s findings, reviewing and editing the manuscript, and supervising the project. Mtalaa WA was responsible for supervising the study and assisting in the validation process. All authors have read and agreed to the published version of the manuscript.
Conflicts of Interest
The authors declared that there are no conflicts of interest regarding the publication of this paper.
Abbreviation List
CODARP, Customer oriented dial-a-ride problem
CPU, Central processing unit
DARP, Dial-a-ride problem
ELEXA, Evolutionary lexicographic algorithm
ELS, Evolutionary local search
HNDS, Hierarchical non-dominated sorting
TTC, Total travel cost
TWT, Total waiting time
References
[1] Dolgui A, Sgarbossa F, Simonetto M. Design and management of assembly systems 4.0: systematic literature review and research agenda. Int J Prod Res, 2022; 60: 184-210.[DOI]
[2] Cordeau JF, Laporte G. A tabu search heuristic for the static multi-vehicle dial-a-ride problem. Transport Res B-Meth, 2003; 37: 579-594.[DOI]
[3] Nasri S, Bouziri H, Aggoune-Mtalaa W. Customer-oriented dial-a-ride problems: A survey on relevant variants, solution approaches and applications. Proceedings of NICE2020 International Conference.[DOI]
[4] Nasri S, Bouziri H, Aggoune-Mtalaa W. An evolutionary descent algorithm for customer-oriented mobility-on-demand problems. Sustain, 2022; 14: 3020.[DOI]
[5] Nasri S, Bouziri H, Aggoune-Mtalaa W. Improving the quality of service within multi-objective customer-oriented dial-a-ride problems. NISS, 2022; 292-305.[DOI]
[6] Bao C, Xu L, Goodman ED et al. A novel non-dominated sorting algorithm for evolutionary multi-objective optimization. J Comput Sci, 2017; 23: 31-43.[DOI]
[7] Nasri S, Bouziri H. Towards a fair mobility: an evolutionary algorithm for customers-dependent transport on demand problems. IINTEC, 2019; 34-40.[DOI]
[8] Curiel-Ramirez LA, Ramirez-Mendoza RA, Bustamante-Bello MR et al. Smart electromobility: Interactive ecosystem of research, innovation, engineering, and entrepreneurship. IJIDeM, 2020; 14: 1443-1459.[DOI]
[9] Monaca U, Bertagna S, Marino A et al. Integrated ship design: An innovative methodological approach enabled by new generation computer tools. IJIDeM, 2020; 14: 59-76.[DOI]
[10] Chevrier R, Liefooghe A, Jourdan L et al. Solving a dial-a-ride problem with a hybrid evolutionary multi-objective approach: Application to demand responsive transport. Appl Soft Comput, 2012; 12: 1247-1258.[DOI]
[11] Molenbruch Y, Braekers K, Caris A et al. Multi-directional local search for a bi-objective dial-a-ride problem in patient transportation. Comput Oper Res, 2017; 77: 58-71.[DOI]
[12] Chassaing M, Duhamel C, Lacomme P. An els-based approach with dynamic probabilities management in local search for the dial-a-ride problem. Eng Appl Artif Intel, 2016; 48: 119-133.[DOI]
[13] Viana RJ, Santos AG, Martins FV et al. Optimization of a demand responsive transport service using multi-objective evolutionary algorithms. GECCO, 2019; 2064-2067.[DOI]
[14] Ren J, Jin W, Wu W. Multi-objective optimization for multi-depot heterogeneous first-mile transportation system considering requests’ preference ranks for pick-up stops. Transportmetrica A, 2022; 1-39.[DOI]
[15] Nasri S, Bouziri H, Aggoune-Mtalaa W. A population-based approach to address real-life transport on-demand problems. GECCO, 2022; 69-70.[DOI]
[16] Chu JC-Y, Chen AY, Shih H-H. Stochastic programming model for integrating bus network design and dial-a-ride scheduling. Transp Lett, 2022; 14: 245-257.[DOI]
[17] Cordeau. Instances of Cordeau. Accessed April 19, 2023. Available at:[Web]
[18] Zitzler E. Evolutionary algorithms for multiobjective optimization: Methods and applications[doctor’s thesis]. Zurich, Swiss: Swiss Federal Institute of Technology Zurich, 1999.
[19] Chassaing. Instances of Chassaing. Accessed July 19, 2020. Available at:[Web]
Copyright © 2024 The Author(s). This open-access article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, sharing, adaptation, distribution, and reproduction in any medium, provided the original work is properly cited.


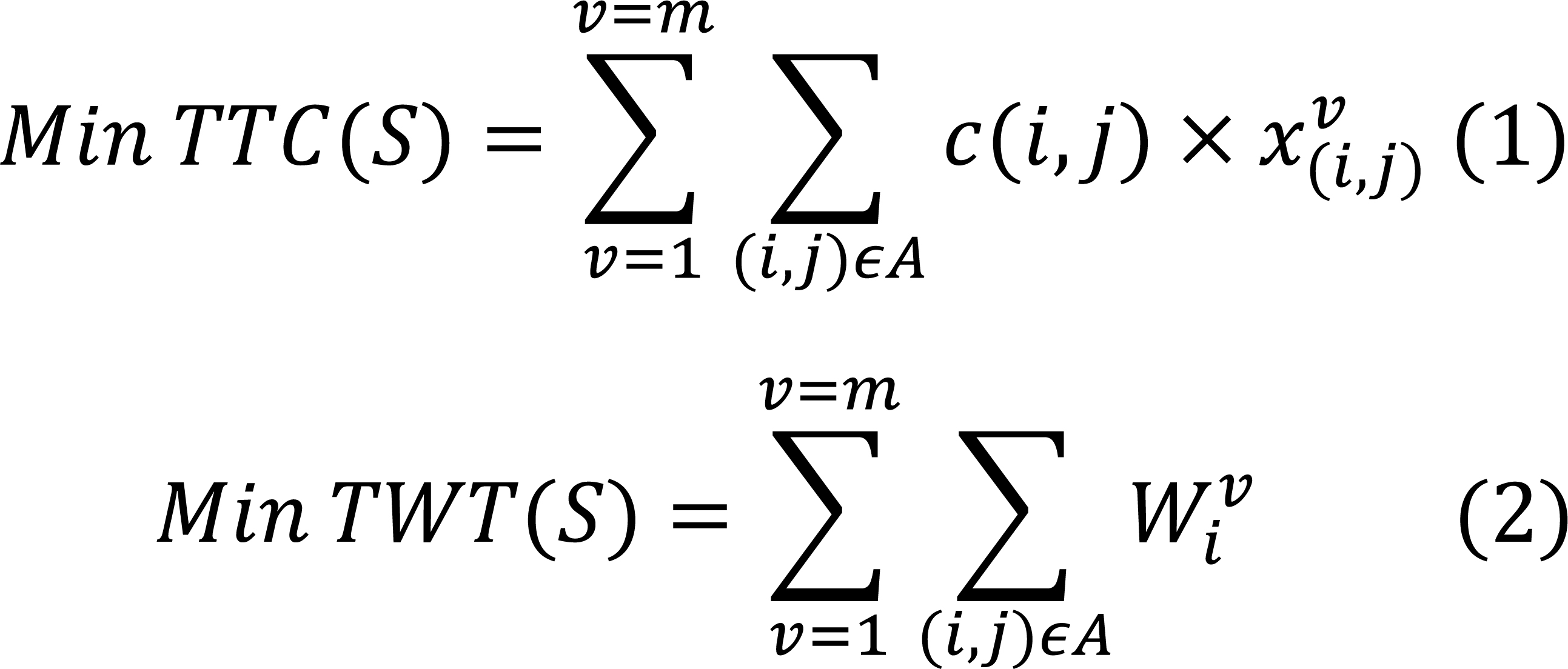




 Copyright ©
Copyright ©