Similarity-based Partitions on Pre-ordered Sets
Carmen Vázquez1*
1Department of Mathematics, University of Vigo, Vigo, Spain
*Correspondence to: Carmen Vázquez, PhD, Professor, Department of Mathematics, Faculty of Economics and Business, University of Vigo, Campus Lagoas-Marcosende, Vigo 36310, Spain; Email: cvazquez@uvigo.es
DOI: 10.53964/mem.2022003
Abstract
Objective: To determine partitions of subsets where a preorder relation and a similarity relation coexist. Each partition-set represents a class of elements that reflects the variety of the whole set, so the similarity relation can be considered to reduce the size of large sets and to handle them more easily. We look at the minimal partitions originated by the similarity relation and compare them using well-established methods.
Methods: A precise definition of the notion of similarity is proposed by unifying two pieces of relevant literature. The similarity-based partitions are mainly compared by using a method called the Rand index and a new method for the subset similarity index.
Results: Looking at the minimal partitions originated by the similarity relation and comparing them using well-established methods, we observed that from an aseptic point of view, there are no essential differences between any of them.
Conclusion: Comparing partitions produced by different methods is an important issue in clustering when comparing results obtained using different methods, parameters or initializations. When the sole objective is the variety offered by the sets in question, any smallest similarity-based partitions can be used to handle large sets. If it becomes necessary to consider the quality of the elements contained in those large sets, then one of them must be chosen specifically.
Keywords: preordered sets, similarity relation, partitions, diversity, cardinal utility
1 INTRODUCTION
Our purpose is to determine a partition of any given set by assigning similar elements of the set to the same subset and dissimilar elements to different subsets. The proposed partition gives rise to multiple sets and shows a number of groups that represents the quality and quantity of each one of these sets. In this way, dealing with large sets becomes easier.
Our research stems from a context in which the degree of freedom that is offered to the consumer must be ranked. A preference relation and a similarity relation between alternatives that are available to a consumer are defined. The consumer must simplify the alternative sets to make pre-ordering between them easier. We believe that these results can be extended to other contexts where there are large sets that must be reduced while maintaining all their characteristics. All that is needed is a pre-order relation between the elements of the universal set and a similarity relation, which can be derived from the pre-order. This similarity relation enables large sets to be reduced in size. Initially, two different methods are used.
In 2000, Pattanaik et al.[1] introduced the concept of similarity as a reflexive, symmetric, but not necessarily transitive binary relation defined by the set of all the alternatives available to the consumer. This notion of similarity is also used in Vázquez[2], but is introduced in a slightly different way. The author initially defines the similarity relation as a relation derived from a preference relation that can be represented by a cardinal utility function, but it is suggested that the concept of similarity be considered as a primitive concept. With this approach, Aizpurua et al.[3] studied the relationship between preferences and similarities. Both papers use this notion to produce partitions of the sets of alternatives to establish and characterize a pre-ordering of those sets. When ranking sets consisting of many elements, it is reasonable to first cluster the elements so as to make the process more practical and tractable. In general, the similarity relation can be used to reduce the size of large sets. Grouping similar elements into smaller sets makes management of large sets much easier.
This paper aims to analyze the partitions of the sets originated by a similarity relation. The similarity notions introduced by Pattanaik et al.[1] and Vázquez[2] differ in that in the former, the similarity notion is a primary notion, while it coexists with the classical preference relation in the later. The first notion suffices if one wishes to study or reflect the variety of elements of the available sets. This paper proposes a precise definition of the notion of similarity by unifying the two versions, and discusses the characterization of the partitions of the sets originating from both papers. The goal is to formulate these concepts in a generalized way. These partitions are compared using a popular method called the Rand index and a new method called the subset similarity index. Some specific examples illustrate these methods and their conclusions. The objective is to determine what kind of partition is the most suitable.
2 METHODS
2.1 Basic Notation and Definitions
Let X be the universal set of basic alternatives or elements. Let Z be the class of all non-empty and finite subsets of X. Let R be a pre-order relation, i.e. a complete, reflexive and transitive binary relation defined on X, where xRy is interpreted as ‘x is at least as good as y’. The indifference relation corresponding to R is denoted by I, while the strict pre-order relation is denoted by P. Even though it is beyond the scope of this paper, it must be borne in mind that the ultimate purpose may be to establish a pre-ordering on Z. At any rate, the ultimate purpose is to make the management of large sets easier.
2.2 The Similarity Relation
Let S be a reflexive, symmetric but not necessarily transitive binary relation defined on X. For all alternatives of x, y∈X, xSy is interpreted as ‘x is similar to y’ and ¬xSy is interpreted as ‘x is dissimilar to y’. Since S is not necessarily transitive, it is possible that y is similar to both x and z, but x is not similar to z. Thus, ‘being similar to’ is not necessarily an equivalence relation. For all A∈Z, A is said to be homogeneous if for all alternatives of a, a'∈A, aSa’. For all x∈X and A∈Z, xSA is written if xSa for all a∈A. Note that if A is homogeneous, xSA if A∪{x} is homogeneous.
In an economic context, a similarity relation can be derived from the agent’s preference relation, assuming that the existence of a cardinal utility represents the preference relation, as was proposed by Vázquez[2]. Consider the case where there exists a function u: X→R that preserves preference orderings (u(x)≥u(y) iff xRy) and describes the intensity of the preference. Assuming that preference can be measured by the agent, those alternatives that differ to a certain degree in utility may be appreciated as similar. This similarity can be represented by a number r>0 determined by the capability of the agent to discern. For all x,y∈X, xSy is interpreted as ‘x is similar to y’ if |u(x)−u(y)|≤r. That relation is referred as a similarity relation derived from the pre-order relation R. Aizpurua et al.[3] argues in favor of the similarity of alternatives. They interpret these relations as a way of modelling the imperfect powers of discrimination of the human mind.
This takes things into a more general framework: Let us consider a pre-ordered set X. In a context where xo∈X⊂Rn is designed as the best element in X, it is possible to consider u(x)=−d(x,xo)=−||x−xo||. Thus, the closer the elements are to the best element, the higher their utility is. Alternatively, if zo∈X⊂Rn is designed as the worst element in X, then it is possible to consider u(x)=d(x,zo)=||x−zo||. Thus, the closer the elements are to the worst element, the lower their utility is. In both cases, the similarity relation derived from the pre-order defines similar elements as elements that are almost the same distance from the best (or the worst) element.
In other contexts, u can be a price function, a cost function or the opposite of one of either. In general, any function u: X→R that measures one or various characteristics or magnitudes that distinguish and define each element of X can be used to define the pre-order relation R, and a similarity relation derived from it.
Other situations consider similarity relations that are not derived from the pre-order relation, as in Pattanaik et al.[1]. In fact, they only use the similarity relation. For example, in a context where X⊂Rn, the similarity relation can be defined as xSy when d(x,y)<r, for any r>0 pre-set. Such a similarity relation is not derived from either of the two pre-order relations defined above.
From a formal point of view, not only is there no need for a ‘cardinal utility’ to construct the similarity relation S, but also fewer restrictions on the pre-order relation are required if it is considered as a primitive notion. When the similarity relation and the pre-order relation coexist, the similarity relation must be compatible with the preference relation. In keeping with this, the following definition is introduced:
Definition 1. A similarity relation S is said to be compatible with a pre-order relation R if for all x,y,z∈X such that xRyRz, xSz implies xSy and ySz.
The notion of similarity defined below and the concept of compatibility of the similarity relation with the pre-order relation that we propose here unify and generalize the frameworks of the two papers referred to above.
Remark 1. Any similarity relation derived from a pre-order relation is compatible with it.
For r>0 and m∈R pre-set, a similarity relation compatible with a pre-order relation R represented by u: X→R would be defined as: xSy when one of these two circumstances occurs:
(1) u(x)>m and u(y)>m
(2) |u(x)−u(y)|≤r, being u(x)≤m or u(y)≤m
Note that, in case X⊂Rn, the similarity relation defined above as xSy iff d(x,y)<r, is not compatible with any of the pre-order relations represented by u(x)=−d(x,xo) or u(x)=d(x,zo).
3 RESULTS AND DISCUSSION
3.1 Similarity-based Partitions
As earlier mentioned, ‘being similar to’ is not necessarily an equivalence relation, but it could define a special partition as defined by Vázquez[2]. Let S be a similarity relation compatible with a pre-order relation R. For all A∈Z, we will write (A)={A1,...,Ak} where A1={a∈A: aSa1}, with a1 being the best element of A according to R; A2={a∈A: aSa2}, with a2 being the best element in A\A1, and so on. To simplify the exposition, R is assumed to be a linear (i.e. antisymmetric) pre-ordering. However, this is not an essential assumption, and it is easy to verify that the results in this paper change only slightly if this assumption is relaxed. As R is a linear pre-ordering, all of these elements ai are well-defined and unique. Vázquez[2] mentions that this partition result is characterized by 5 properties. Here, we present the proof of this characterization and comment on an example.
Theorem 1. The partition result (A) is the unique class {A1,...,Ak} that verifies the following statements:
(A.1) A1,...,Ak are all non-empty and homogeneous subsets of A
(A.2) A1 ∪...∪ Ak=A
(A.3) A1,...,Ak are pairwise disjoint
(A.4) if i<j, then xPy, for all x∈Ai, y∈Aj
(A.5) for each y∈Aj, if i<j, then there exists x∈Ai such that ¬xSy
Proof: For each finite subset A of X, A∈Z, (A) verifies all the statements described. This part of the proof is straightforward.
Now suppose that (A)={B1,...,Bl} is a partition of A verifying the 5 statements described above. Note first that a1∈B1, from (A.2) and (A.3), there exists a unique i such that a1∈Bi, if i>1 (A.4) leads to the contradiction that xPa1 for all x∈Bi−1.
To show that B1⊂A1, consider b∈B1 and suppose ¬b∈A1. Then b∈Ai for a unique i>1 and, by (A.5), there exists x∈A1 such that ¬xSb. Moreover, by (A.4), xPb. Otherwise, as a1RxPb and a1Sb, then the compatibility of the similarity relation implies that xSb. This contradiction means that b∈A1. Analogously, A1⊂B1, thus B1=A1.
By an analogous argument, it can be proved that if Bj=Aj, for j=1,...,i, then Bi+1=Ai+1. Finally, k=l because Bi=Ai, for all i=1,...,min{k,l} and A1 ∪...∪ Ak=B1 ∪...∪ Bl=A.
We use a very simple example to illustrate this kind of partition.
Example 1. Let A={x,y,z} such that xPyPz, xSy, ySz and ¬xSz, then (A)={{x,y},{z}}. Note that the partition {{x},{y,z}} does not satisfy (A.5).
Pattanaik et al.[1] used the name similarity-based partition (SP) of A for any class of sets {A1,...,Ak} that verifies (A.1), (A.2) and (A.3), i.e. partitions formed by homogeneous subsets. They consider the set of all smallest similarity-based partitions (SSP) of A in the sense of cardinality, i.e. partitions (A) of A such that, for every similarity-based partition '(A) of A, #'(A)≥#(A). Consequently, all the partitions of the same set that they name as SSP have the same cardinal. In fact, the pre-order of opportunity sets that they propose is established by contrasting this cardinal. Thus, they consider the minimals of all similarity-based partitions of A with respect to the cardinal. It can be observed that the maximal is the trivial partition, which comprises the singletons, UT(A)={{a}: a∈A}. Note that A is homogeneous if and only if the unique SSP of A is {A}.
In example 1, all SSP of A taken into consideration by Pattanaik et al.[1] are {{x,y},{z}} and {{x},{y,z}}. Vázquez[2] considers the similarity-based partitions used by Pattanaik et al.[1] that verify 2 more statements. The 4th statement (A.4) requires elements to be grouped in sets A1,...,Ak according to the pre-ordering R, with the elements grouped in Ai being preferred to those grouped in later sets. This condition is useful when sets need to be compared after they are clustered according to similarities, taking into account the quality of the clusters as well as their quantity.
The 5th statement (A.5) requires the incorporation of each element in set Ai with the smallest index i possible in reference to the similarity relation. This condition is illustrated in the example above, where the element y must be included in A1 for this statement to be complied with. The 5th statement also implies that the union of two sets Ai and Aj is not homogeneous, which guarantees that it is the best possible cluster of similar elements.
Vázquez[2] calls the partition that complies with all the statements above the best smallest similarity-based partition (BSSP) of A, (A). Note that the BSSP of any set A is a SSP of A. An example that illustrates these two concepts is presented.
Remark 2. This case illustrates the difference between the BSSP and other SSPs. Let A,B∈Z. To construct a SSP of A∪B, elements of set A must be distributed among the subsets of an initial SSP of B, picking them out as being similar to the subset where they are added. If the idea is for the new partition of A∪B to be the BSSP, then a BSSP of B must be chosen and the elements of A must be added to the subset with the lowest index among the similar subsets (provided there are several subsets).
3.2 Comparing Similarity-based Partitions
In this section, we contrast the SSP partitions of the same set that are allowed by Pattanaik et al.[1], including the BSSP partition considered by Vázquez[2]. We compare them in an aseptic way with regards to the pre-order and similarity relations. Comparing partitions produced by different methods is an important issue in clustering when comparing results obtained by different methods, parameters or initializations. A well-established method for comparing partitions is the Rand index, described in Rand[4], and a more recent method is the subset similarity index described by Runkler[5]. The first of these methods focuses on the similarity in the distribution of elements and the second on the similarity in the distribution of subsets. A brief description of these indexes is provided and their usage in comparing SSP partitions in some illustrative examples.
The Rand index measures the similarity between any two partitions of the same set X, U and U* (note that both partitions describe the same number of objects, n=#X, but may have a different number of subsets, k and k*) by considering all pairs of objects and distinguishing 4 cases. The number of pairs of elements that belong to the same subset in U and the same subset in U* is denoted as n1. Pairs of elements that belong to the same subset in U and different subsets in U* and pairs of elements that belong to different subsets in U and the same subset in U* are also considered. The number of such cases is denoted as n2 and n3, respectively. Finally, the number of pairs of elements that belong to different subsets in the two partitions is denoted as n4.
Based on these cases, the Rand index is defined as R(U,U*)=(n1+n4)/(n1+n2+n3+n4).
Obviously, 0≤R(U,U*)=R(U,U*)≤1 and R(U,U)=1. R and Rand[4] asserts that R(U,U*) is closer to 1 when U and U* are more similar to one another.
We present a numerical example to compare some SSP partitions by using the R and index.
Example 2. Consider the ordered set M={0,1,2,4,5,8,9,12}, where the elements are in decreasing order, with the similarity relation S defined by xSy if |x − y|≤ 3. The BSSP of M is
(M)={{0,1,2},{4,5},{8,9},{12}}
and the other SSPs of M are
U1={{0,1},{2,4,5},{8,9},{12}}
U2={{0,1},{2,4},{5,8},{9,12}}
U3={{0},{1,2,4},{5,8},{9,12}}
When these partitions are compared via the Rand index, it turns out that the most similar are U2 and U3. In fact, if n1=3, n2=1, n3=2, n4=22, then R(U2,U3)=25/28. Analogously, the Rand indexes for the rest of the pairs of partitions are obtained as R(U1,U3)=R((M),U3)=20/28, R((M),U1)=24/28, R((M),U2)=21/28 and R(U1,U2)=23/28. Hence the least similar pairs of partitions are (U1,U3) and ((M),U3), even though they are all very similar. This is because to change one into the other, only a small number of elements must be transferred.
This example helps to draw a general conclusion. Usually, this happens with all SSP of the same set X. In fact, if n1+n2+n3+n4 is the number of all pairs of elements of X, i.e. the number of binary subsets of X,
|
then R(U,U*)=2(n1+n4)/(n(n−1)), where n=#X. When U and U* are SSP, all pairs of dissimilar elements are placed in different subsets in the two partitions (thus they always account for n4), and most pairs of similar elements must be placed together in pre-order to keep the cardinal of U and U* constant and minimal (thus most of them appear in n1 and reduce the value of n2 and n3). Hence, if U and U* are SSP, n1+n4 do not differ enough and the values of n2 and n3 are low, which always gives a similar and high Rand index. From this, we can conclude that:
Remark 3. The Rand index indicates that all SSP of the same set are quite similar.
This argument does not hold when U and U* are only SP, as in the case of the trivial partition. In one particular case, we compute this index between any partition U={C1,...,Ck} and the trivial partition UT of a set X. In this case, n1=n3=0,
|
and n4=c1(c2+...ck)+c2(c3+...ck)+...+ck-1ck=
|
being ci=#Ci and n=#X. Then
|
Reverting to numerical example 2 above, by comparing all the SSP with the trivial partition, R(U1,UT(M))=R(U3,UT(M))=R(Φ(M),UT(M))=23/28 and R(U2,UT(M))=24/28 are obtained. Again, they are all very similar because all the subsets in the partitions have only two or three elements. This is not always the case, as not all SP are so similar. This is illustrated in the next example.
Example 3. Consider the case of a set A formed by n+1 elements so that φ(A) includes only two subsets, one of which is a singleton. That is, the case of a set with all but one of the elements being similar. In this case, A=A1∪{a}, with A1 being homogeneous and ¬aSa', for all a'∈A1. Then R(Φ(A),UT(A))=2/(n+1). In this case, it can be checked that the Rand index is lower, as the cardinal of A is higher. In fact, the increase in the cardinal of A makes Φ(A) more different from the trivial partition because it results in more elements in A1. Thus, the Rand index between SP turns out to be very low.
In the same vein, we analyze these partitions by using the subset similarity index. The subset similarity index introduced by Runkler[5] is based on similarities in the subsets of the partitions. Consider a pair of partitions U={C1,...,Ck} and U*={C*1,...,C*k*} of the same set X, the size similarity of two subsets Ci and C*j, with i∈{1,...,k}, j∈{1,...,k*} is defined as sij=(#(Ci∩C*j))/( #(Ci∪C*j)).
The subset similarity index is defined by:
|
As with the R and index, 0≤S(U,U*)=S(U*,U )≤1 and S(U,U)=1. Runkler[5] asserts that S(U,U*) is closer to 1 when U and U* are more similar.
Example 4. When the partitions in numerical example 2 are compared using the subset similarity index, U1 and (M) are found to be the most similar. For U1 and (M), the following calculations are made:
s11= 2/3 |
s21= 1/5 |
s31= 0 |
s41= 0 |
max si1= 2/3 |
s12=0 |
s22=2/3 |
s32=0 |
s42=0 |
max si2= 2/3 |
s13=0 |
s23=0 |
s33=1 |
s43=0 |
max si3= 1 |
s14=0 |
s24=0 |
s34=0 |
s44=1 |
max si4= 1 |
max s1j= 2/3 |
max s2j= 2/3 |
max s3j= 1 |
max s4j= 1 |
|
Thus, S(U1,(M))=2/3. The rest of the indexes are computed similarly to obtain S(U1,U2)=S((M),U2)=S(U1,U3)=S((M),U3)=1/3 and S(U2,U3)=1/2. A comparison of the subsets that form the partitions reveals that the most similar pairs or partitions are U1 and (M), followed by U2 and U3. Recall that these two pairs of partitions are also the most similar according to the Rand index.
Computing this index between any partition U={C1,...,Ck} and the trivial partition UT of any set X, it is found that S(U,UT)=1/max j=1,...,k cj. Thus, in our example, S(U1,UT(M))=S(U3,UT(M))=S((M),UT(M))=1/3 and S(U2,UT(M))=1/2. Recall that these two pairs of partitions are also the most similar according to the Rand index too.
Finally, in the case of the set in example 3, A=A1∪{a}, with A1 being homogeneous, #A1=n and ¬aSa', for all a'∈A1, it is found that S((A),UT(A))=1/n. The test was performed again, but using this index this time around. It was found that an increase in the cardinal of A caused a decrease in the similarity of (A) to the trivial partition.
The subset similarity index is consistent with the conclusions obtained using the Rand index.
4 CONCLUSION
Applying the Rand index and the subset similarity index to the examples that have been studied reveals that all the partitions considered by Pattanaik et al.[1] are similar. Among those partitions, the one used by Vázquez[2] is no different from the others.
Consequently, when the sole objective is the variety offered by the sets in question, then the establishment of any SSP is helpful in the handling of large sets. If it becomes necessary to consider the quality of the elements contained in those large sets, then the BSSP must be chosen, i.e. the partition characterized by the 5 properties described above.
Acknowledgments
Not applicable.
Conflicts of Interest
All authors declared no conflict of interest.
Author Contribution
Vázquez C solely contributed to this manuscript.
Abbreviation List
BSSP, Best smallest similarity-based partition
SP, Similarity-based partition
SSP, Smallest similarity-based partitions
References
[1] Pattanaik PK, Xu Y. On diversity and freedom of choice. Math Soc Sci, 2000; 40: 123-130. DOI: 10.1016/S0165-4896(99)00043-8
[2] Vázquez C. Ranking opportunity sets on the basis of similarities of preferences: a proposal. Math Soc Sci, 2014; 67: 23-26. DOI: 10.1016/j.mathsocsci.2013.11.001
[3] Aizpurua JM, Nieto J, Uriarte JR. Choice procedure consistent with similarity relations. Theor Decis, 1990; 29: 235-254. DOI: 10.1007/BF00126804
[4] Rand WM. Objective criteria for the evaluation of clustering methods. J Am Stat Assoc, 1971; 66: 846-850. DOI: 10.1080/01621459.1971.10482356
[5] Runkler TA. Comparing partitions by subset similarities, International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems, Springer, Berlin, Heidelberg, Germany, June 28-July 2, 2010. DOI: 10.1007/978-3-642-14049-5_4
Copyright ©2022 The Author(s). This open-access article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, sharing, adaptation, distribution, and reproduction in any medium, provided the original work is properly cited.

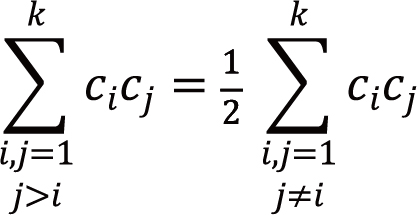



 Copyright ©
Copyright ©