Development of Generalized Correlations for Predicting Density and Specific Heat of Nanofluids for Enhanced Heat Transfer
Ghulam Habib1, Tauseeq Hussain1, Mustafa Kilic2, Atta Ullah1*
1Department of Chemical Engineering, Pakistan Institute of Engineering and Applied Sciences, Islamabad, Pakistan
2Department of Mechanical Engineering, Adana Alparslan Turks Science and Technology University, Adana, Turkey
*Correspondence to: Atta Ullah, PhD, Department of Chemical Engineering, Pakistan Institute of Engineering and Applied Sciences, Lehtrar Rd Nilore, Islamabad, 45000, Pakistan; Email: atta@pieas.edu.pk
DOI: 10.53964/jmn.2024003
Abstract
Objective: Energy-generating devices such as automotive vehicles, power reactors, computing machines etc. require effective cooling for safe and efficient operation. Additionally, at the same time, heat losses must be minimized. In industry, pure fluids such as water, air etc. are usually used for these purposes. Nanofluids have recently been explored as an alternative to traditional coolants. Nanofluids have attracted attention due to their superior thermophysical properties as compared to conventional fluids. Nanofluids are nanosized particles of metallic, non-metallic, or organic origin suspended in base fluids. Some examples of these nanoparticles include silver, copper, metal oxides, metal nitrides, carbon materials (such as carbon nanotubes, metal carbides) etc. Several options for base fluids exist, such as ethylene glycol, water, transformer oil, etc.
Methods: The thermophysical properties of nanofluids of interest include thermal conductivity, viscosity, density, and specific heat. Predicting these physical properties, which depend upon particle concentration, temperatures, particle sizes, etc., is a significant challenge. Researchers have developed correlations for predicting these properties based on available experimental data. However, a thorough literature review suggests that generalized correlations do not exist, especially for the density and specific heat. Most researchers have done work on thermal conductivity and viscosity. The present work has developed generalized correlations to predict nanofluids' thermophysical properties density, and specific heat. Experimental data was collected for the various operating and geometric parameters affecting nanofluids' density and specific heat.
Results: By performing regression analysis, four dimensionless correlations are proposed for each of predicting two important thermophysical properties, i.e., heat capacity and density of nanofluids. The developed correlations were compared with available experimental data.
Conclusion: It was found that the correlations generated were fitted the experimental data for density and specific heat with an accuracy of ±10% band of actual value.
Keywords: nanofluid, nanoparticle, base fluid, thermal conductivity, thermophysical properties
1 INTRODUCTION
According to the first law of thermodynamics, energy must be transferred to the system to get work from it. Energy can be transferred either through heat or in the form of work. The heat exchange between the two systems can occur due to temperature differences. Heat transfer is the subject that gives information about the mode and rate of transfer of thermal heat transfer. Heat transfer applications can be found everywhere, from large-scale industrial processes, including power generation, chemical, and biochemical processes, etc., to small household appliances. Heat has to be dissipated rapidly from most electronic devices for efficient performance[1]. With the evolution in technology, the compactness of these devices has been enhanced, which demands a more efficient heat transfer transmission and cooling management system[2]. Conventional heat transfer fluids, such as water, methanol, ethylene glycol, etc., have lower thermal properties; thus, they cannot dissipate heat rapidly. The solids have higher thermal properties than conventional fluids. With this motivation, Maxwell gave the idea of enhancing the thermal properties of conventional fluids by dispersing microscale solid particles in them[3,4].
The rapid settling of microscale particles in the base fluid can cause clogging in the flow path inside the channel. To address this problem, Choi introduced the concept of nanofluids. Nanofluid is a suspension of nanoparticles such as ZnO, TiO2, etc. of size less than 100nm in a fluid-based fluid like water, ethylene glycol, etc[5]. Due to the nanoparticle's smaller size, the flow channels cannot be clogged. Nanofluids have superior thermophysical properties to conventional heat transfer fluids, and thus, they rapidly dissipate heat[6,7].
Nanofluids have demonstrated their effectiveness as lubricants in machining systems. Moreover, nanofluids have lower pumping power than traditional heat transfer fluids[8,9]. In addition, there has been a substantial utilization of nanofluids in enhancing renewable energy applications for energy purposes[10]. The thermophysical properties include thermal conductivity, viscosity, specific heat, and density. The factor affecting these thermophysical properties are temperature, volume fraction, Brownian motion, length of nanolayer, the diameter of nanoparticle, etc[6]. Most of the existing theoretical and experimental correlations for predicting these thermophysical properties do not include all these factors in the literature. The main inspiration behind the nanofluids was the enhancement of thermal conductivity by dispersing solid particles in the base fluid, so most of the work has been done on determining the empirical correlations for the thermal conductivity, and after that, researchers have prioritized developing viscosity correlations. Very little work has been done on determining correlations for specific heat and density[6,7,11].
For determining the heat transfer characteristics of water based nanofluids of TiO2 and Al2O3 at low particle volume concentration Pak and Cho proposed an equation similar to the Dittus Boelter correlation[12]:
|
Nunf, Nusselt number
Renf, Reynolds
Prnf, Prandtl numbers
Nunf is a function of Renf and Prnf which are further functions of operating conditions such as average velocity, tube diameter and thermophysical properties of the nanofluid such as density, viscosity, specific heat, and thermal conductivity. So, for determining the heat transfer characteristics accurately, determination of the thermophysical properties is necessary.
The heat diffusion thorough the material is dictated by thermal diffusivity (α) and it is a function of thermal conductivity, density, and specific heat of the fluid. For determining nanofluid thermal diffusivity following formula can be used[13]:
|
αnf, Thermal diffusivity
Knf, Thermal conductivity
⍴nf, Density
Another important property kinematic viscosity (Ɵ) is often used for finding fluid the relative change in momentum to its relative ability to sustain the momentum by inertia dynamic viscosity ɳ acts as a messenger for the propagating message of momentum disturbance inside the fluid while due to the presence of fluid inertia acts to sustain its momentum. Inertia is proportional to fluid mass, and mass is proportional to the density. For finding the nanofluid kinematic viscosity, accurate determination of the nanofluid density is required[13].
|
ɵnf, Kinematic viscosity
ɳnf, Inertia dynamic viscosity
⍴nf, Density
Heat distribution from the source heat transfer fluids is circulated through the pipes and heat transfer equipment with the help of pumps. The pumping power is used for overcoming the energy losses due to fluid friction. In order to calculate the pressure loss in a conduit of length L the following equation can be used[14]:
|
∆p, Pressure drop
⍴nf, Density
f, Darcy friction factor
L, Length
v, Velocity
d, Diameter
Where f can be calculated by using following equation[15]:
|
f, Darcy friction factor
Re, Reynolds
These are some of the utilities of the basic thermophysical properties discussed and can be utilized in thermodynamics, heat transfer, .and fluid flow applications. From this discussion, it can be concluded that accurate determination of nanofluids, density, and specific heat is as important as thermal conductivity, and viscosity determination for getting the true picture of hydrodynamics, heat transfer, and thermodynamic analysis.
2 METHODS
First, detailed literature studies related to thermophysical properties of interest (density and specific heat) were studied. After that, the potential factors affecting each thermophysical property were identified and were nondimensionalized. Also, experimental data related to each thermophysical property was collected as explained in Tables 1 and 2. In the end, regression analysis was performed on each thermophysical property. To access results, goodness of fit indicators was calculated and the experimental and predicted value of each property of interest was compared by parity chart. Summary of methodology is explained in Figure 1.
Table 1. Experimental Database for Density
Reference |
Dataset Type |
Nanoparticle |
Base Fluid |
f T(K) |
No. of Data points |
[16] |
Development |
Fe3O4 |
Water |
0-2 293-333 |
24 |
[17] |
Development |
Al2O3 |
Water |
0.0386-0.538 303-313 |
6 |
[17] |
Development |
MWCNT |
Water |
0.016-0.45 303-313 |
6 |
[17] |
Development |
CuO |
Water |
0.021-0.298 303-313 |
6 |
[17] |
Development |
MgO |
Water |
0.029-0.54 303-313 |
6 |
[17] |
Development |
TiO2 |
Water |
0.036-0.3978 303-313 |
6 |
[17] |
Development |
ZnO |
Water |
0.0198-0.35 303-313 |
6 |
[18] |
Development |
CQDS |
Water |
0.2-1 283-353 |
75 |
[19] |
Development |
Al2O3 |
Water |
0.05-4 297.2-313 |
16 |
[19] |
Development |
SiO2 |
Water |
0.05-4 297.2-313 |
16 |
[19] |
Development |
TiO2 |
Water |
0.05-4 297.2-313 |
16 |
[20] |
Development |
Al2O3 |
Water |
0.128-0.389 283-313 |
21 |
[21] |
Development |
Al2O3 |
Water |
1.34-4.33 298 |
3 |
[22] |
Development |
TiN |
EG/Water (40/60, v/v) |
0.25-1 293.15-333.15 |
20 |
[22] |
Development |
TiN |
EG/Water (60/40, v/v) |
0.25-1 293.15-333.15 |
20 |
[23] |
Development |
Al2O3 |
EG/Water (60/40, w/w) |
1-10 273-323 |
36 |
[23] |
Development |
Sb2O5:SnO2 |
EG/Water (60/40, w/w) |
1-5.8 273-323 |
30 |
[23] |
Development |
ZnO |
EG/Water (60/40, w/w) |
1-7 273-323 |
42 |
[24] |
Test |
Al2O3 |
Water |
0-4 277.4-313 |
56 |
[25] |
Test |
Al2O3 |
Water |
0.1-2 293-333 |
15 |
Table 2. Specific Heat Experimental Database
Reference |
Dataset Type |
Nanoparticle |
Base Fluid |
f T(K) dp(nm) |
No. of Data points |
[14] |
Development |
Al2O3 |
Propylene Glycol (PG) |
0.5-2 239.2-363 15 |
39 |
[14] |
Development |
Al2O3 |
PG |
0.5-4 239.5-362 20 |
65 |
[14] |
Development |
Al2O3 |
PG |
0.5-6 239.5-362 45 |
78 |
[14] |
Development |
ZnO |
PG |
0.5-4 239.5-362 36 |
65 |
[14] |
Development |
TiO2 |
PG |
0.5-1.5 239.5-360 15 |
39 |
[14] |
Development |
CuO |
PG |
0.5-6 239.5-360 30 |
78 |
[26] |
Development |
Al2O3 |
Methanol |
0-0.25 278-298 10 |
30 |
[27] |
Development |
AIN |
EG |
0-3.64 288.15-308.15 20&50 |
30 |
[27] |
Development |
SI3N4 |
EG |
0-3.5 288.15-308.15 20&80
|
30 |
[27] |
Development |
TIN |
EG |
0-2.31 288.15-308.15 20 & 80 |
30 |
[28] |
Development |
CuO |
Water |
0-0.4 293 50 |
5 |
[29] |
Development |
Al2O3 |
Water |
2.5 298-323 13 |
6 |
[16] |
Development |
Fe3O4 |
Water |
0-2 293-333 13 |
24 |
[21] |
Development |
TiO2 |
Water |
0.99-4.35 300 27 |
4 |
[30] |
Development |
Al2O3 |
Water |
1.36-6.56 308-328 50 |
12 |
[30] |
Development |
CuO |
Water |
4-13.7 308-328 30 |
12 |
[31] |
Development |
CuO |
Water |
0.4-2 298-337 37 |
103 |
[31] |
Development |
CuO |
EG |
0.4-3 296-337 37 |
84 |
[32] |
Development |
Al2O3 |
Water |
3.7-9.3 296-336 50 |
105 |
[32] |
Development |
Al2O3 |
EG |
1-8.1 296-336 50 |
105 |
[33] |
Development |
Al2O3 |
Water |
1-5 293 80 |
5 |
[25] |
Test |
Al2O3 |
Water |
0.5 305-308 45 |
7 |
[21] |
Test |
Al2O3 |
Water |
1.34-4.33 300 13 |
3 |
[29] |
Test |
TiO2 |
Water |
0.99-4.35 300 27 |
4 |
[34] |
Test |
CuO |
Water |
0.1-0.6 293 50 |
6 |
[35] |
Test |
Al2O3 |
EG |
1-5 293-350 10 |
144 |
[35] |
Test |
Al2O3 |
Water |
2-5 293-350 10 |
196 |
[35] |
Test |
CuO |
Water |
0.24-4 293-350 29 |
44 |
|
Figure 1. Sketch of the proposed methodology.
2.1 Existing Correlation for Predicting Density
The density of nanofluid can be calculated by application of mixture law that the following equation can expressed as:
|
⍴nf, Density
⍵, Volume Fraction
In the above equation, ⍴ represent density and subscripts n, p and f are used for nanofluid, particle and base fluid, respectively. ⍵ can be defined as the ratio of the volume of the particle to the total volume of a mixture, including base fluid and dispersed particle. It can give accurate predictions at low volume fraction of solid particles for the most cases[11].
2.2 Existing Correlations for Predicting Specific Heat
It is the heat required to change the substance's temperature by one degree. For measuring specific heat, a calorimeter used. A mixture rule similar to density calculates the specific heat of nanofluid[21].
|
Cp, Specific heat
⍵, Volume Fraction
The subscripts n, p, and f are used for nanofluid, particle, and base fluid representation. Another relationship can be used for volumetric heat capacity with the thermal equilibrium assumption[6].
|
After simplification,
|
The main potential factors affecting the specific heat of nanofluids are temperature, the concentration of the nanoparticle inside the base fluid, and the particle size of the nanoparticle. Specific heat is enhanced by increasing temperature and concentration[6]. Researchers have given contradictory results on the effect of particle size on the specific heat[36].
The density and specific heat theoretical correlations do give explicit dependence of temperature. The specific heat correlations also do not give dependence on the particle size .The correlations mentioned above also have applicability range limitations, so a new wide range of experimental data-based models are required[11,37].
The following goodness of fit indicators was employed to check the accuracy of the developed correlation[38].
Coefficient of determination (R2)
It shows the dependence of a dependent variable on an independent variable, and it can be calculated by using this formula.
|
R2, Coefficient of determination
yi, Observed value
yf, Fitted or predicted value
ym, Mean value of yi dataset.
The value of R2 lies between 0 and 1.
Adjusted R2 (R2adj)
The value of R2 is increased with the increment in the number of independent variables, so it does not truly reflect the significance of independent variables. The R2adj reflects the significance of each predictor, and this relation can define as.
|
R2, Coefficient of determination
R2adj, Adjusted R2
sp, Sample size
p, Number of independent variables.
Mean square error and root mean square error
The following equations calculate the MSE and RMSE:
|
sp, Sample size
yi, Observed value
yf, Fitted or predicted value
|
Both the value of MSE and RMSE should be less for a good fit.
Standard error of estimate (SEE)
The standard error of estimate gives information about the deviation between the observed value and the regression line.
|
MS, Mean square
ESS it is given by the following equation:
|
df, Degree of freedom
sp, Sample size
k, Independent variables.
|
MS, Mean square
df, Degree of freedom
Mean absolute percentage error (MAPE)
|
sp, Sample size
yi, Observed value
yf, Fitted or predicted value
2.3 Development of Generalized Correlation for Density by Regression Analysis
Based on literature studies density of nanofluid was considered to follow the functional form as:
|
⍴n, Density
f, Darcy friction factor
T, Temperature
The above-mentioned individual parameters were normalized to form the functional form in terms of non-dimensional parameters. Volume percent is a non-dimensional quantity, while the remaining quantities were made non-dimensional by joining each parameter with its counter parameter. Nanofluid density and particle density were made non-dimensional by dividing with the density of base fluid. To make the temperature unitless, it was divided by the reference temperature. As there was no such parameter in the functional form that had no counter parameter, Pi theorem was not applied deliberately, and following the simplified approach gave the simple, functional form. Similarly, an approach was followed for developing the Propylene glycol and Ethylene glycol /Water (60:40) generalized density correlation[39]. Satti et al.[14] developed the generalized correlation for Propylene Glycol nanofluid specific heat by simply normalizing the parameters. The density and specific heat values of base fluids were taken from[8].
|
ρ, Density
f, Volume percent of nanoparticles inside the nanofluid
Tref, A reference temperature taken as 293K.
Correlation was developed after regression analysis and, coefficients are given in Table 3.
|
f, Volume percent of nanoparticles inside the nanofluid
ρ, Density
T, Temperature
Table 3. Density Correlation Regression Coefficients
Coefficients |
Value |
A0 |
1.02914 |
A1 |
0.133336 |
A2 |
0.0121617 |
A3 |
-1.58613 |
A4 |
-0.0219706 |
A5 |
-0.000158899 |
A6 |
0.0000851985 |
2.4 Development of Generalized Correlation for Specific Heat by Regression Analysis
Based on a literature study related to the nanofluids, specific heat was expressed in function form as:
|
f, Volume percent of nanoparticles inside the nanofluid
ρ, Density
T, Temperature
d, Diameter
The parameters mentioned above were normalized to form a functional form in terms of non-dimensional parameters. This functional form was formed and explained as:
|
f, Volume percent of nanoparticles inside the nanofluid
ρ, Density
T, Temperature
d, Diameter
dref, Diameter that is equal to 100nm.
100nm is considered as the upper limit of nanometer size, and to keep uniformity, this particle size was selected as the reference diameter. Following correlation was developed to predict specific heat and, coefficients used in correlation are given in Table 4.
|
f, Volume percent of nanoparticles inside the nanofluid
ρ, Density
T, Temperature
d, Diameter
dref, Diameter that is equal to 100nm.
Table 4. Specific Heat Correlation Regression Coefficients
Coefficients |
Value |
Bo |
-3.10199 |
B1 |
-6.58459 |
B2 |
-1661.92 |
B3 |
2.93518 |
B4 |
-0.0317963 |
B5 |
-0.123952 |
B6 |
16.828 |
B7 |
-0.0826509 |
B8 |
-0.0000190467 |
B9 |
-83.2218 |
B10 |
101.683 |
B11 |
-12.3911 |
B12 |
0.223112 |
B13 |
-6.70652 |
B14 |
-0.00463471 |
B15 |
0.0000161367 |
B16 |
0.153006 |
B17 |
8.52055 |
B18 |
-0.260192 |
B19 |
-0.372595 |
B20 |
0.000255654 |
B21 |
0.31103 |
3 RESULTS AND DISCUSSION
3.1 Density
The statistical analysis of the developed regression model reveals that the value of R2 is equal to 0.988635. That means a 98.86% variance in ⍴eff is predicted by the selected independent variables. Moreover, the value of R2adj 0.98844 is close to the value of the determination coefficient, and it represents the dependence of ⍴eff on the added independent variables is quite significant. The results also show that the developed generalized correlation fits the data used for developing the regression model with the values of other goodness of fit like MS, RMS, SEE and MAPE as 0.000053, 0.00729, 0.00736 and, 0.47%. The lower values of the RMS, SD and MD show the high accuracy of the developed correlation. The maximum percentage difference of 2.56% was obtained for Al2O3/water at 297.92K and 4 volume percent.
The developed correlation was applied to the data not used in the regression model development to verify the generalized correlation's accuracy. The statistical goodness of fit MS, RMS, SEE and MAPE values were determined as 0.000046, 0.0068, 0.0070, and 0.38%. The maximum percentage difference 2.195% was found for TiO2/water at 298K and vol 4.4%. The parity charts for development and tested data as shown in Figure 2 were plotted with a bound of ±10% and 100 percent data lies within this bound for both cases.
|
Figure 2. Comparison of Experimental and Predicted Effective Density of Nanofluids. A: Effective density development dataset parity chart; B: Effective density test dataset parity chart.
3.2 Specific Heat
After the nonlinear regression analysis was performed on the development data, goodness of fits was calculated. The closeness of the R2 and R2adj 0.865 and 0.863 reveals that the model high dependent on the selected independent variables. The other goodness of fit parameter’s MS, RMS, SEE and, MAPE lower values 0.001378, 0.0371, 0.0375 and 3.23% represent the high accuracy of the developed correlation. The max percentage difference of 17% was found for TiN/EG at 308.15K, volume percent 2.31% and 20nm particle size.
The developed correlation was applied on the tested dataset for validating the accuracy of the developed correlation, and goodness of fit parameters MS, RMS, SEE and MAPE were calculated as 0.000592, 0.0243, 0.0250 and 1.98%. These lower values show the high accuracy of the developed correlation. The maximum percentage difference was found for Al2O3/water 12.26% at 293K, vol 4.33% and 13nm.
The parity chart was plotted between the experimental and predicted values of the effective specific heat for the development as shown in Figure 3 with a bound of ±10%. In the development data, 97% of data lies within the set bound and 99.2% data of the tested dataset lies within the set bound.
|
Figure 3. Comparison of Experimental and Predicted Effective Specific Hear of Nanofluids. A: Effective specific heat development dataset parity chart; B: Effective specific heat development dataset parity chart.
4 CONCLUSION
In this work, regression analysis was performed over the wide range of experimental data to develop generalized correlations for density and specific nanofluids heat. The experimental data was divided into the development and tested data sets. The regression analysis was performed over the development data, and correlations for density and specific heat were developed within bounds of ±10%. The developed correlation validity was checked using the tested dataset, and the proposed correlations fitted the tested datasets within the set respective bound for the density and specific heat.
Acknowledgements
Authors acknowledge the support received from PIEAS.
Conflicts of Interest
The authors declare that they have no competing interests.
Author Contribution
Habib G was responsible for writing, and original draft. Hussain T was responsible for reviewing and revising the manuscript. Both first and second authors carried out the literature review and research work. Kilic M and Ullah A contributed by supervising, visualizing and reviewing the manuscript. All authors contributed to the manuscript and declare no conflict of interest.
Abbreviation List
MAPE, Mean absolute percentage error
MS, Mean square
MSE, Mean squared error
RMS, Root mean square
RMSE, Root mean squared error
SD, Standard Deviation
SEE, Standard error of estimate
References
[1] Goga G, Afridi S, Mewada C et al. Heat transfer enhancement in solar pond using nano fluids. Mater Today: P, 2023.[DOI]
[2] Ho MLG, Oon CS, Tan LL et al. A review on nanofluids coupled with extended surfaces for heat transfer enhancement. Results Eng, 2023; 17: 100957.[DOI]
[3] Arora N, Gupta M. An updated review on application of nanofluids in flat tubes radiators for improving cooling performance. Renew Sust Energ Rev, 2020; 134: 110242.[DOI]
[4] Ali ARI, Salam B. A review on nanofluid: preparation, stability, thermophysical properties, heat transfer characteristics and application. SN Appl Sci, 2020; 2: 1-17.[DOI]
[5] Kalsi S, Kumar S, Kumar A et al. Thermophysical properties of nanofluids and their potential applications in heat transfer enhancement: A review. Arab J Chem, 2023; 16: 105272.[DOI]
[6] Gupta M, Singh V, Kumar R et al. A review on thermophysical properties of nanofluids and heat transfer applications. Renew Sust Energ Rev, 2017; 74: 638-670.[DOI]
[7] Vandrangi SK, Hassan S, Sharma KV et al. Effect of base fluids on thermo-physical properties of SiO2 nanofluids and development of new correlations. Math Method Appl Sci, 2020; 1-34.[DOI]
[8] Wang X, Song Y, Li C et al. Nanofluids application in machining : a comprehensive review. Int J Adv Manuf Tech, 2023; 131: 3113-3164.[DOI]
[9] Patel J, Soni A, Barai DP et al. A minireview on nanofluids for automotive applications: Current status and future perspectives. Appl Therm Eng, 2023; 219: 119428.[DOI]
[10] Bhatti MM, Vafai K, Abdelsalam SI. The Role of Nanofluids in Renewable Energy Engineering. Nanomater, 2023; 13: 2-5.[DOI]
[11] Ullah A, Kilic M, Habib G et al. Reliable prediction of thermophysical properties of nanofluids for enhanced heat transfer in process industry: a perspective on bridging the gap between experiments, CFD and machine learning. J Therm Anal Calorim, 2023; 148: 5859-5881.[DOI]
[12] Pak BC, Cho YI. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Exp Heat Tran Int J, 1998; 11: 151-170.[DOI]
[13] Ali HM. Advances in Nanofluid Heat Transfer, 1st ed. Elsevier: Amsterdam, Nederland, 2022.
[14] Satti JR, Das DK, Ray D. Specific heat measurements of five different propylene glycol based nanofluids and development of a new correlation. Int J Heat Mass Tran, 2016; 94: 343-353.[DOI]
[15] Dix A, Kim S. A novel friction factor model for wire-wrapped rod bundles. Nucl Eng Des, 2023; 401: 112104.[DOI]
[16] Sundar LS, Singh MK, Sousa ACM. Investigation of thermal conductivity and viscosity of Fe3O4 nanofluid for heat transfer applications. Int Commun Heat Mass, 2013; 44: 7-14.[DOI]
[17] Shoghl SN, Jamali J, Moraveji MK. Electrical conductivity, viscosity, and density of different nanofluids: An experimental study. Exp Therm Fluid Sci, 2016; 74: 339-346.[DOI]
[18] Mirsaeidi AM, Yousefi F. Viscosity, thermal conductivity and density of carbon quantum dots nanofluids: an experimental investigation and development of new correlation function and ANN modeling. J Therm Anal Calorim, 2021; 143: 351-361.[DOI]
[19] Said Z, Saidur R. Thermophysical Properties of Metal Oxides Nanofluids. Nanofluid Heat and Mass Transfer in Engineering Problems. IntechOpen: London, UK, 2017.[DOI]
[20] Teng TP, Hung YH. Estimation and experimental study of the density and specific heat for alumina nanofluid. J Exp Nanosci, 2014; 9: 707-18.[DOI]
[21] Pak BC, Cho YI. Hydrodynamic and Heat Transfer Study of Dispersed Fluids With Submicron Metallic Oxide Particles. J Therm Energy Transport Storage Conversn, 2013; 11: 37-41.[DOI]
[22] Akilu S, Baheta AT, Sharma KV. Characterization and modelling of density, thermal conductivity, and viscosity of TiN–W/EG nanofluids. J Therm Anal Calorim, 2020; 140: 1999-2010.[DOI]
[23] Vajjha RS, Das DK, Mahagaonkar BM. Density Measurement of Different Nanofluids and Their Comparison With Theory. Petrol Sci Technol, 2009; 27: 612-624.[DOI]
[24] Ho CJ, Liu WK, Chang YS et al. Natural convection heat transfer of alumina-water nanofluid in vertical square enclosures: An experimental study. Int J Therm Sci, 2010; 49: 1345-1353.[DOI]
[25] Heyhat MM, Kowsary F, Rashidi AM et al. Experimental investigation of turbulent flow and convective heat transfer characteristics of alumina water nanofluids in fully developed flow regime. Int Commun Heat Mass, 2012; 39: 1272-1278.[DOI]
[26] Mostafizur RM, Saidur R, Aziz ARA et al. Thermophysical properties of methanol based Al2O3 nanofluids. Int J Heat Mass Tran, 2015; 85: 414-419.[DOI]
[27] Żyła G, Vallejo JP, Lugo L. Isobaric heat capacity and density of ethylene glycol based nanofluids containing various nitride nanoparticle types: An experimental study. J Mol Liq, 2018; 261: 530-539.[DOI]
[28] Chein R, Chuang J. Experimental microchannel heat sink performance studies using nanofluids. Int J Therm Sci, 2007; 46: 57-66.[DOI]
[29] Hussein AM, Bakar RA, Kadirgama K et al. Experimental measurement of nanofluids thermal properties. Int J Automo Mech E, 2013; 7: 850-863.[DOI]
[30] O’Hanley H, Buongiorno J, McKrell T et al. Measurement and Model Validation of Nanofluid Specific Heat Capacity with Differential Scanning Calorimetry. Adv Mech Eng, 2012.[DOI]
[31] Barbés B, Páramo R, Blanco E et al. Thermal conductivity and specific heat capacity measurements of CuO nanofluids. J Therm Anal Calorim, 2014; 115: 1883-1891.[DOI]
[32] Barbés B, Páramo R, Blanco E et al. Thermal conductivity and specific heat capacity measurements of Al2O3 nanofluids. J Therm Anal Calorim, 2013; 111: 1615-1625.[DOI]
[33] Murshed SMS. Simultaneous measurement of thermal conductivity, thermal diffusivity, and specific heat of nanofluids. Heat Transfer Eng, 2012; 33: 722-731.[DOI]
[34] Zhou LP, Wang BX, Peng XF et al. On the specific heat capacity of CuO nanofluid. Adv Mech Eng, 2010; 2: 172085.[DOI]
[35] Popa CV, Nguyen CT, Gherasim I. New specific heat data for Al2O3 and CuO nanoparticles in suspension in water and Ethylene Glycol. Int J Therm Sci, 2017; 111: 108-115.[DOI]
[36] Munyalo JM, Zhang X. Particle size effect on thermophysical properties of nanofluid and nanofluid based phase change materials: A review. J Mol Liq, 2018; 265: 77-87.[DOI]
[37] Akilu S, Sharma KV, Baheta AT et al. A review of thermophysical properties of water based composite nanofluids. Renew Sust Energ Rev, 2016; 66: 654-678.[DOI]
[38] Gogtay NJ, Deshpande SP, Thatte UM. Principles of regression analysis. J Assoc Phys India, 1961; 124: 251-252.
[39] Satti JR, Das DK, Ray DR. Measurements of Densities of Propylene Glycol-Based Nanofluids and Comparison with Theory. J Therm Sci Eng Appl, 2016; 8 021021.[DOI]
Copyright © 2024 The Author(s). This open-access article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, sharing, adaptation, distribution, and reproduction in any medium, provided the original work is properly cited.



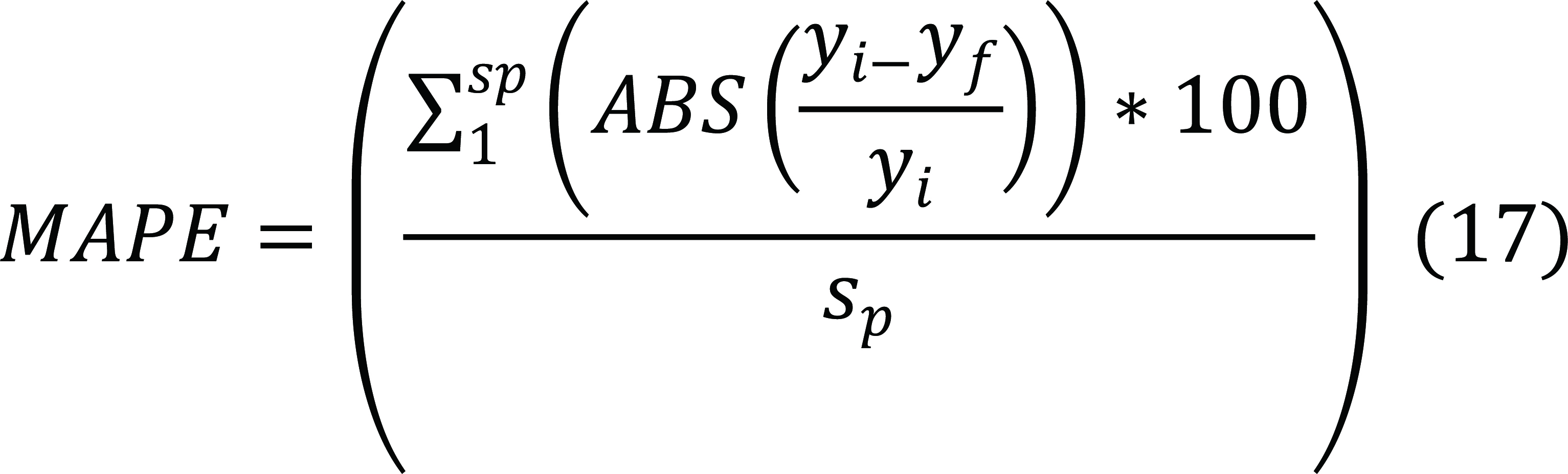





 Copyright ©
Copyright ©