Analysis of Thermal Isotropy of Parallelepiped Shape of Bronze Samples for Mechanical Engineering Applications

 

Ziyovuddin Nizomov1, Shahnavoz Sodatdinov1, Rahim Saidzoda2, Dilshod Nematov3*

 

1Tajik National University, Dushanbe, Tajikistan

2M.S. Osimi Tajik Technical University, Dushanbe, Tajikistan

3S.U. Umarov Physical-Technical Institute of NAST, Dushanbe, Tajikistan

 

*Correspondence to: Dilshod Nematov, PhD, Head of Laboratory, Laboratory of Quantum Electronics, S.U. Umarov Physical-Technical Institute of National Academy of Sciences of Tajikistan, Dushanbe, 734042, Tajikistan; Email: dilnem@mail.ru

 

DOI: 10.53964/jmim.2024009

 

Abstract

Objective: The need to find out whether the specimens are ‘thermally thin’ or not is the basis for applying the law of conservation of energy or the Fourier differential equation of heat conduction in finding the time dependence of the specimen temperature. The aim of this study is to find out the thermal field distribution in a parallelepiped shaped bronze specimen and to verify the Bio number.

 

Methods: A number of external variables make it difficult to maintain a monotonic change in sample temperature during the ‘heating’ stage. These factors led to the use of the cooling method to study tiny samples with low inertia of the thermal process. We used the cooling method to experimentally verify the isotropy of the thermal field in the sample and to study the kinetics of cooling relative to the sample axes over a wide range of temperatures.

 

Results: It was found out that in natural air cooling the main mechanisms are conductive, convective and radiative heat transfer. The contribution of thermal radiation to the cooling process is noticeable at high temperatures. It was found that the typical cooling time increases with sequential radiative, conductive and convective heat transfer. By extending the temperature study area to, for the first time, we were able to observe each component of the heat transfer process independently. The values of the typical cooling time on all axes correspond to the experimental error bounds. It was found that the temperature value of the sample is independent of the coordinates and depends only on time. In this case, the law of conservation of energy can be used to explain the dependence of body temperature on cooling time.

 

Conclusion: It is shown that the sample under study is ‘thermally thin’, i.e. the thermal field is constant in all directions. In this situation, the thermal balance equation should be applied rather than the Fourier differential equation of heat conduction, since the temperature gradient inside the body is practically zero. The results obtained are of great importance for the study of cooling processes of metallic products in thermal power engineering, heat engineering and thermophysics.

 

Keywords: cooling method, cooling kinetics, bronze, heat transfer, temperature dependence

 

1 INTRODUCTION

Every year in the research laboratory “Condensed Mater Physics” named after Professor Narzullaev B.N. Research Institute of Tajik National University, our research group conducts studies of the cooling kinetics of metal samples using a single thermocouple, i.e. investigate the temperature only along the axis of the cylinder[1-10]. It was of interest to find out whether the sample temperature depends on the coordinate. For this purpose, the cooling kinetics of a bronze specimen formed from parallel cylinders of width 2.4cm, length 4.2cm, and thickness 0.9cm with respect to the x, y, and z axes was investigated.

 

Heating or cooling of bodies in a medium of constant temperature is a practically significant problem of non-uniform heat conduction. Thermal similarity criteria include the Biot and Fourier criteria. The Biot number is the ratio of the rate of conductive heat transfer to the rate of energy storage in the material[11-15].

 

 

where λ is the heat transfer coefficient of the body material and α is the heat transfer coefficient from the body surface to the environment. It is possible to determine whether a body has a constant temperature by the Bio number.

 

The ratio of the rate of heat transfer to the rate of energy storage in a material is known as the Fourier number. For a temperature of 600K, the total heat transfer coefficient of bronze is α≈60W/(m K), the heat transfer coefficient at room temperature λ≈64W/(m K) and V/S=0.283cm Fourier number Bi≈0.00265[16,17]. This shows that the Bi number for our sample is low (Bi≥0.1). A Bi number less than 0.1 means that the substance is “thermally thin” and the temperature can be considered constant throughout the entire volume of the material.

 

At each moment of time, the temperature inside such a body has time to equalise due to intensive heat exchange by heat conduction. Since the temperature gradient inside the body is practically zero, instead of the Fourier differential equation of heat conduction we will have the heat balance equation. The reduction of energy accumulated in a solid body should be equal to the heat flux removed from the surface by convection[13,17]:

 

 

where C, ρ V, S, T are, respectively, specific heat capacity, density, volume, area and temperature of the sample, α is the heat transfer coefficient, Ts is the ambient temperature.

 

The solution of Equation (1) has the form[1]:

 

 

In Equation (2) the value

 

 

 

has a time dimension. At τ=τi, the temperature difference between the sample and the environment decreases by a factor of 2.71. We use the value of τi as a typical cooling time in cooling procedures because it depends on the sample material and the heat transfer method.

 

Taking into account radiative, conductive and convective heat transfer, Equation (2) takes the following form[18]:

 

 

where indices i, t and k indicate radiative, conductive and convective heat transfer, (∆Tt)τ=0, (∆Tk)τ=0 - temperature difference between the heated body and the environment at τ=0, (∆Ti)τ=0 - the temperature difference between the heated body at the moment of measurement start and the temperature at which radiation stops, τi, τt and τk - characteristic cooling times for heat transfer processes by radiation, heat conduction and convection.

 

The temperature of the sample can be found at any time by Equation (4), which is an approximate solution of the unsteady heat conduction problem associated with the cooling of bodies in a medium with constant temperature. Thus, Equation (4) describes the similarity equation at small values of the Bi number in the process of free cooling.

 

The values of the characteristic cooling time are determined experimentally. Let us introduce the cooling time to τi ratio as a number

 

 

In the case of radiative heat transfer, a radiation Bio number is introduced, defined by the formula Bii=σT3V/λS, where σ-degree of blackness[19].

 

The maximum temperature of the aluminium specimens was 620°C. They exhibit radiant heat transfer as well as conductive-convective (collective) heat transfer. By extending the temperature study area, we were able to observe each heat transfer component independently for the first time, as Equation (4) shows. In the heat transfer process between the sample and air, heat crosses the solid-gas barrier. Heat is first transferred to the mid-temperature region by a process known as thermodiffusion, which involves the movement of heat particles. Convection, which occurs in the surrounding medium, the air, is then used to transfer the heat. The indices i, t and k have been replaced by 1, 2 and 3 to simplify the notations. According to the analysis of literature data, the topic of scale dependence of thermophysical properties of materials still remains practically unexplored. This once again confirms the relevance of the chosen problem: at the time of the beginning of this work, systematic experimental studies of the dependences of the thermophysical characteristics of metallic samples on the coordinate have not been recorded in the literature.

 

2 EXPERIMENTAL METHOD

The cooling method was chosen to investigate the time dependence of the sample temperature. This method is based on the Newton-Richman law of external heat conduction. Measurement of the sample temperature from the cooling time was carried out on the installation, the principle of operation of which is described in detail in[7,20]. The relative error in temperature measurement was ±1% between 40° and 400°C and 2.5% between 400° and 1000°C. From the recorded sample temperature, we subtracted the outside air temperature, represented as ∆T=T-T0. We then plotted ∆T=f(τ), which represents the temperature difference as a function of time. Processing of all measured data was done on a computer using Microsoft Office Excel application. Sigma Plot 10 tool was used for plotting and processing of graphs.

 

3 RESULTS AND DISCUSSION

The cooling method was used to study the effect of the temperature of parallel bronze specimens on the cooling time over a wide range of temperatures with respect to three axes.

 

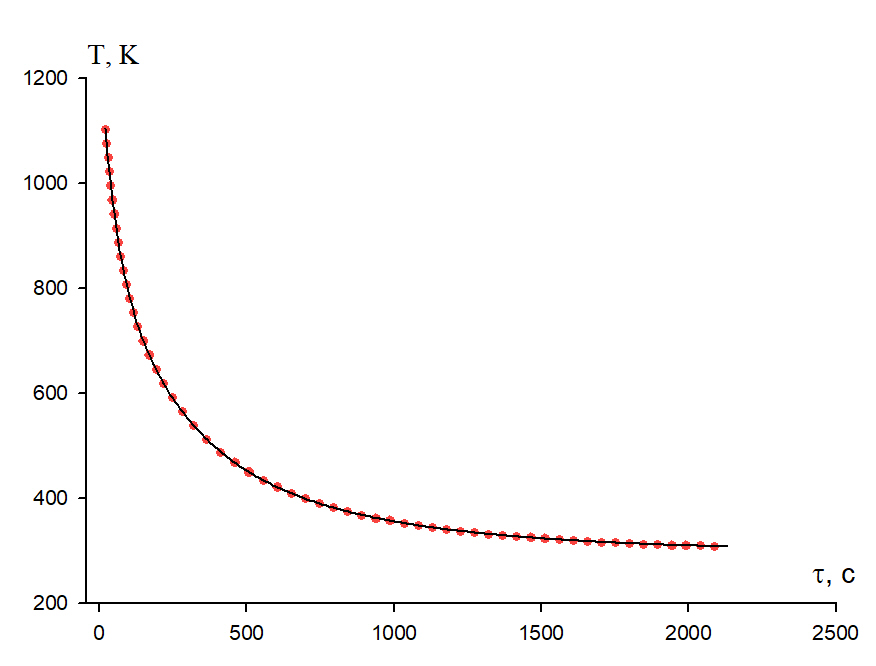
As an illustration, Figure 1 shows how the temperature of a bronze specimen varies as a function of cooling time along the z-axis. The results of processing the graphs according to Equation (4) using the Sigma Plot 10 programme, the regression coefficient, the values of the parameters contained in Equation (4) and the standard error are given below the Tables 1-3.

 

Figure 1. Temperature dependence of the bronze sample on the cooling time relative to the z-axis.

 

Tables 1-3 show the results of graph processing using Sigma Plot 10 programme: regression coefficient, the value of parameters entering Equation (4) and standard error.

 

Table 1. Results of Processing Figure 1

Notes: Regression coefficient, value of parameters entering Equation (4) and standard error.

 

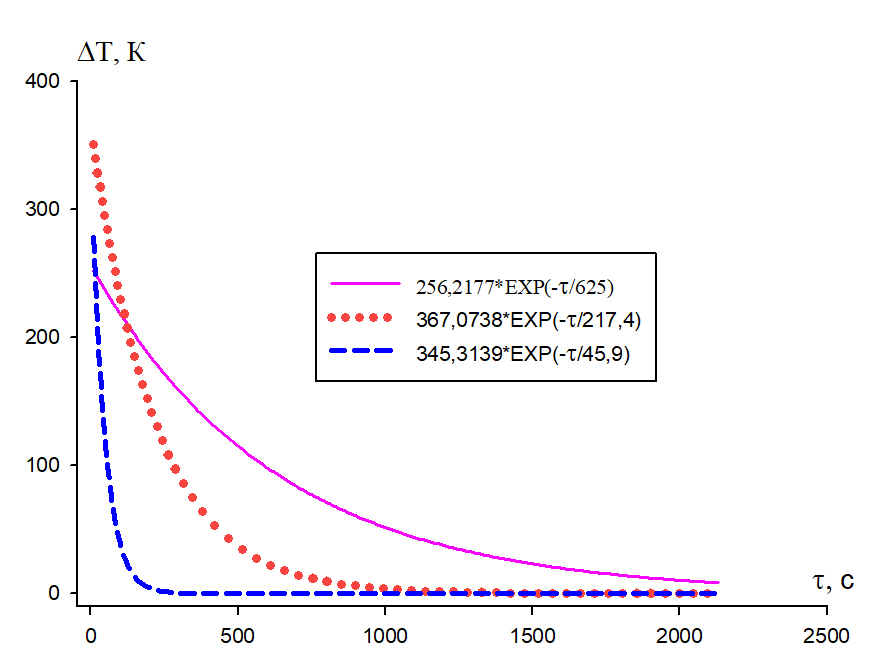
Figure 2 shows the cooling curves due to radiation, conductive and convective heat transfer.

 

Figure 2. Dependence of the bronze sample temperature on the cooling time with respect to the z-axis as a result of convection (purple), heat conduction (red) and thermal radiation (blue).

 

Table 2. Results of Processing Figure 3

Notes: Regression coefficient, value of parameters entering Equation (4) and standard error.

 

 

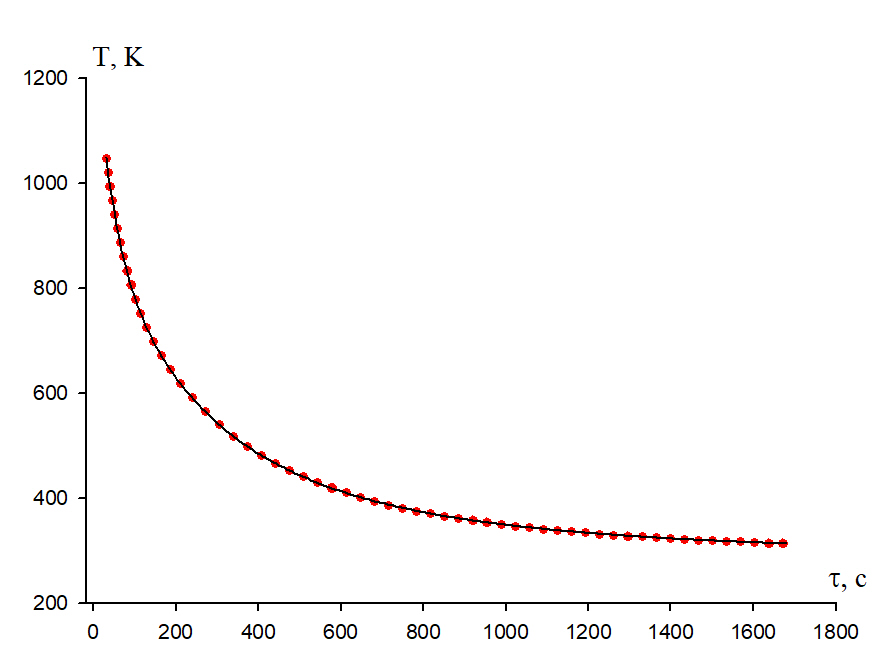
The relationship between sample temperature and cooling time along the x-axis is shown in Figure 3.

 

Figure 3. Relationship between the sample temperature and cooling time along the x-axis.

 

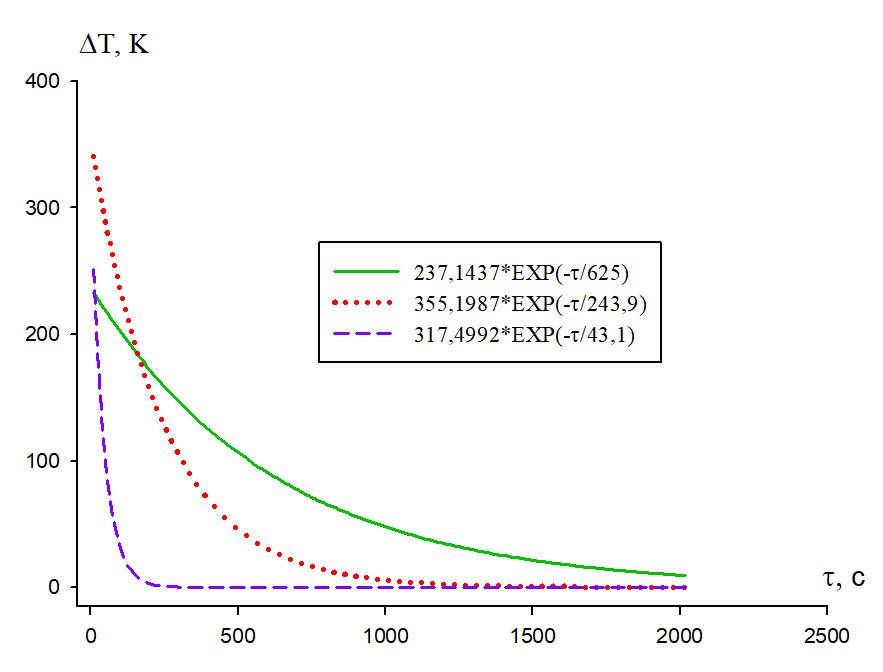
Figure 4 shows the cooling curves due to radiation, conductive and convective heat transfer.

 

Figure 4. Dependence of the sample temperature on the cooling time with respect to the x-axis due to thermal radiation (blue), heat conduction (red) and convection (green).

 

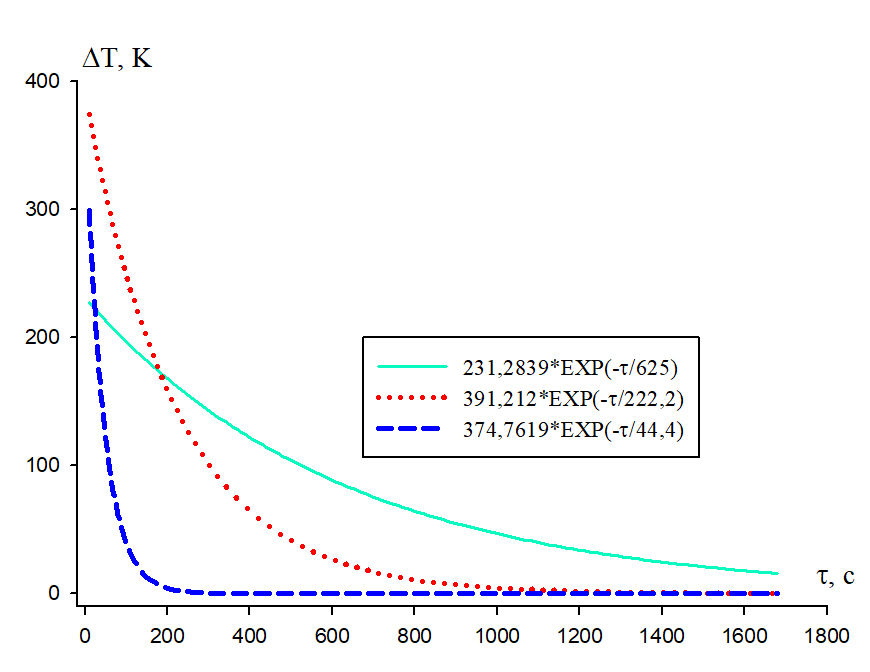
The relationship between sample temperature and cooling time in the z direction is shown in Figure 5.

 

Figure 5. Temperature dependence of the bronze sample on the cooling time with respect to y-axis.

 

Table 3. Results of Processing Figure 5

Notes: Regression coefficient, value of parameters entering Equation (4) and standard error.

 

Figure 6 shows the cooling curves due to thermal radiation, conductive and convective heat transfer.

 

Figure 6. Dependence of the sample temperature on the cooling time relative to the y-axis due to thermal radiation (blue), heat conduction (red) and convection (green).

 

Table 4 shows a comparison of the values of the parameters included in Equation (4) for the three axes.

 

Table 4. Comparison of Values of Characteristic Cooling Times

 

The results presented in Figures 1, 3 and 5 and Tables 1-4 show that the cooling of the sample is time-dependent, not direction-dependent. The values of typical cooling time for each axis are the same within experimental error. The results indicate that the sample is ‘thermally thin’, that is, the temperature value depends only on time and not on coordinates. The dependence of the body temperature on the cooling time in this case can be explained by the law of conservation of energy, and Equation (4), which we came to when processing the data, makes sense.

 

4 CONCLUSION

The time dependence of the body temperature of a parallelepipedal bronze specimen on the axis orientation was investigated. It was found out that convective heat exchange, air conduction and air radiation contribute to the cooling of the specimens. In the order of increasing radiative, conductive and convective heat transfer, the characteristic cooling time increases. At high temperatures, the role of thermal radiation in the cooling process becomes evident.

 

The results of the work are of great importance for understanding the processes occurring during the cooling of metal products. The physics of thermal processes and the application of similarity theory to them are interested in the found dependences of cooling kinetics on the direction. Experimental studies have shown that convective, radiative and conductive heat transfer are the main processes of natural air cooling. Radiative, conductive and convective heat transfer were found to have typical cooling times that increase.

 

Acknowledgements

The work was performed at the S.U. Umarov Physical-Technical Institute of the National Academy of Sciences of Tajikistan with the support of International Science and Technology Center (ISTC), project TJ-2726.

 

Conflicts of Interest

The authors declared that they have no known competing financial interests or personal relationships.

 

Author Contribution

Nizomov Z. supervised the research, methodology, formal analysis, data processing and writing of the original version of this article. Shahnavoz S. conducted experiments and assisted with writing. Rahim S. and D. Nematov assisted with review and editing, supervision and methodology. The final version of the manuscript was approved by all authors.

 

Data Availability Statement

The data presented in this study are available in article.

 

References

[1] Nizomov Z, Turakhasanov IT, Faizieva MR. Influence of the size of aluminium samples on the kinetics of their cooling and heat transfer processes. Bulletin of the Tajik Nat U. S Nat Sci, 2022; 1: 165-177.

[2] Turakhasanov IT, Nizomov Z, Sodatdinov ShS et al. Effect of the size of AV98 aluminium cylindrical specimens on the cooling kinetics. Mater Endless Light Sci, 2022; 2022: 123-129.

[3] Sharipov JG, Nizomov Z, Saidzoda RH. Thermophysical properties of doped rare-earth metal alloy Zn55Al. Bulletin of the Tajik Nat U. S Nat Sci, 2024; 3.[DOI]

[4] Nizomov Z, Mirzoev FM. Temperature dependence of heat capacity and thermodynamic functions of aluminium, iron, silicon, zinc, copper, magnesium, manganese and titanium. Bulletin of the Tajik Nat U. S Nat Sci, 2019; 1: 122-128.

[5] Sodatdinov SS, Nizomov Z, Gulov BN et al. Thermal isotropy of parallelepiped bronze specimens. Endless Light Sci, 2022; 17: 79-87.

[6] Gulov BN, Nizomov Z, Tabarov FS. Thermophysical properties of aluminium of grade A5N and its alloys doped with silicon, copper and rate-earth metals. Metallofiz Nov Tekh, 2021; 43: 1553-1562.[DOI]

[7] Nizomov Z, Avezov ZI, Saidov RH et al. Thermal Properties of Zn5Al and Zn55Al Alloys with II A Group Elements. Key Eng Mater, 2022; 99: 76-84.[DOI]

[8] Nizomov Z, Mirzoev FM, Avezov ZI et al. Estimation of the contribution of heat radiation and convective heat exchange for aluminium of various degrees of purity with natural air heat discharge. Endless Light Sci, 2022; 15-16: 131-140.

[9] Nizomov Z, Turakhasanov I, Saidzoda RKh et al. Effect of Size on Cooling Kinetics of Spherical Samples from Different Grades of Aluminium. Eng Sci Technol, 2024; 512: 418-426.[DOI]

[10] Nematov DD, Burhonzoda A, Khusenov MA et al. The quantum-chemistry calculations of electronic structure of boron nitride nanocrystals with density Functional theory realization. Egyptian Journal of Chemistry, 2019; 62: 21-27.[DOI]

[11] Mikheev MA, Mikheeva IM. Fundamentals of Heat Transfer. Bastet: Moscow, Russia, 2010.

[12] Dulnev GN. Theory of heat and mass transfer. NIU ITMO: Saint Petersburg, Russia, 2012.

[13] Gukhman AA. Application of similarity theory to the study of heat and mass transfer processes: Transfer processes in a moving medium. Izd-vo LKI: Moscow, Russia, 2018.

[14] Leontiev AI. Theory of Heat and Mass Transfer. (3rd ed.) Izd-vo MSTU named after N.E. Bauman: Moscow, Russia, 2018.

[15] Ivanov ID, Ereschenko VE. Methods of similarity of physical processes. MADI: Moscow, Russia, 2015.

[16] Kikoin IK. Tables of physical quantities. Moscow: Atomizdat, Russia, 1976.

[17] Wong H. Basic formulae and data on heat exchange. Atomizdat: Moscow, Russia, 1979.

[18] Nizomov Z, Sodatdinov Sh, Saidzoda R. K, Nematov D. Influence of the Height Value of Cylindrical Specimens of Copper Grade M3 on the Kinetics of Their Cooling and Heat Transfer Processes. Eng Sci Technol, 2024; 5: 316-325.[DOI]

[19] Sparrow EM. Heat Transfer by Radiation. RD Sess: trans. from English. Edited by Blokh AG. Energia Leningr Department: Leningrad, Russia, 1971.

[20] Nizomov Z, Gulov B, Saidov RH et al. Measurement of specific heat capacity of solids by cooling method. Bulletin of Nat U, 2010; 3: 136-141.

 

Copyright © 2024 The Author(s). This open-access article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, sharing, adaptation, distribution, and reproduction in any medium, provided the original work is properly cited.