Coupled Models in Complex Systems Related to Smart Electromagnetic Energy Procedures
Adel Razek1*
1Group of Electrical Engineering - Paris (GeePs), CNRS, University of Paris-Saclay and Sorbonne University, Gif-sur-Yvette, France
*Correspondence: Adel Razek, DSc, Professor, Group of Electrical Engineering - Paris (GeePs), CNRS, University of Paris-Saclay and Sorbonne University, F91190, Gif-sur-Yvette, France; Email: adel.razek@centralesupelec.fr
Abstract
This contribution aims to evaluate and analyze the significance of coupling models in the operation of intelligent electromagnetic (EM) energy procedures for complex systems (CSs). It encompasses strategies for coupling CSs models, reviews of coupled and reduced models, intelligent supervision and management of CSs models in EM energy procedures, and their applications.The article begins by introducing the supervision and management of EM CSs. It delves into the governing equations of the EM phenomenon, providing a detailed explanation. The coupling of the EM phenomenon with other physical phenomena in external components is then analyzed and reviewed. These components are interconnected and together form a CS in the EM energy procedure. The coupling of equations governing the external phenomena with those governing the EM phenomenon is elaborated upon. Subsequently, the article presents intelligent supervision of EM energy procedures for both simple systems and CSs. For CSs, the concept of a digital twin and the concept of pairing in automated procedures are thoroughly analyzed and discussed. Following this, the management of CSs models in energy procedures is examined. This includes the adaptation of complete coupled models to optimize control speed in the procedure, which is analyzed and considered through the concept of model reduction. Finally, the article focuses on applications of CSs in EM energy procedures, particularly in the context of electric and intelligent vehicles and their management.
Keywords: complex systems, electromagnetic, smart procedures, models coupling, supervision, model managing
1 INTRODUCTION
Complex systems (CSs) have emerged as a prominent area of research, encompassing a wide range of disciplines including natural sciences, engineering, social sciences and societal concerns. They manifest complexity in diverse domains,from natural sciences as neuroscience[1] and Earth’s climate[2], to space vehicles[3] , computer vision[4], fair division economics[5], game theory of strategic interactions[6] and political science[7].
CSs exhibit intricate and nonlinear behaviors, consisting of interconnected subsystems. CSs exhibit variability across vast spatial and temporal scales, with dynamic phenomena at different scales influencing one another. Therefore, the spatial and temporal multiscale nature is a defining characteristic of CSs and plays a crucial role in understanding complexity. These sytems present dissipative arrangements generated resulting from non-linear energy exchanges that impact the relationship between materials, data, and their environment. Analyzing CSs from a multiscale perspective involves exploring connections between phenomena at different scales, understanding the interplay of distinct governance mechanisms, examining the coupling between spatial and temporal structural variations, and addressing concerning phenomena that occur within CSs. To tackle these challenges, a multiobjective variational formulation can be employed to study and analyze CSs.
Coupling in CSs can be approached using two distinct methodologies[8]. The first is a model-centered method, which assumes prior knowledge of the physical mechanisms that drive the complex phenomena and their interaction relationships. The other is a model-free methodology that relies on statistical estimates of dependence. It disregards the specific physical mechanisms and instead analyzes the characteristics of the data and their probability distributions.
In recentenergy procedures, CSs play a crucial role, particularly in relation to electromagnetic (EM) energy[9]. Sophisticated control tools supervise these procedures, which operate judiciously[10]. The performance of control systems in these cases relies heavily on the accuracy of the system model. The modeling of EM systems, which are often associated with other phenomena, requires considering the interactions among all these phenomena. The precision of the system model, necessary for the control, requires the coupling of the different involved phenomena[11]. However, this coupling can be complex due to the nonlinearities involved, resulting in increased computation time, which is a disadvantage for real-time control. Actually, the model nature of a system involved in an automated energy procedure depends on two factors, the closeness to the reality and the computing time needed for its execution. Indeed, a precise model with small computing time permits a swift control with minimum iterations, which corresponds to an optimal control of the procedure. The conduct of such process is influenced by the sensors, control and system model. The characters of these elements directly affect the procedure real time matching. Balancing the trade-off between model precision and computation time depends on the complexity of the system and the matching technology used. In such cases, a numerical strategy for model reduction should be employed. In such a case, a model reduction numerical strategy should be practiced[12,13]. Such reduction is intended to maintain key aspects of the overall system behavior. It is important to note that model coupling primarily pertains to the physical phenomena involved, whereas model reduction is mainly concerned with numerical strategies. Such reduction aims to conserve accuracy while only affecting unnecessary numerical portions of the model[14].
Numerous studies have been conducted in the field of CSs. However, this proposed contribution distinguishes itself from existing literature by presenting a comprehensive strategy for each aspect of the topic. The objective of this work is the evaluation and the analysis of the coupling of models of CSs within the framework of intelligent EM energy procedures. This involves a strategy of coupling of CSs models as well as a review of coupled and reduced models, intelligent supervision and management of CSs models in EM energy procedures and their applications focusing on electric vehicles.
The content of the paper is summarized in this sense. In the second section, the supervision and management of EM CSs will be introduced. The third section details the governing equations of the EM phenomenon. In the fourth section, the coupling of the EM phenomenon with other physical phenomena involved in external components will be illustrated and reviewed. These components are associated and form a CS in the EM energy procedure, the coupling of the equations governing the external phenomena with that of the EM is detailed and conferred. The fifth section exposes the intelligent supervision of EM energy procedures for simple and complex cases. For the case of CSs, the concept of digital twin (DT) and pairing in automated procedures are analyzed and conferred. Section six studies the management of the models of CSs in the energy procedures. The adaption of the complete coupled model, to optimize the speed of control of the procedure, will be analyzed and considered through the notion of model reduction. The seventh section presents applications on CSs in EM energy procedures focusing on electric and intelligent vehicles and their managements. The final section discusses different details relative to the questions treated in the paper sections. The conclusions summarize the contributions of the study and offer recommendations for further research.
2 SUPERVISION AND MANAGEMENT OF EM CSs
Modern energy procedures have become crucial in our daily lives, and these procedures increasingly rely on smart automated processes. heavily relies on advanced computer and mathematical tools that are available. These sophisticated tools enable real-time simulation of the physical properties of the systems, which is essential for effective control and management. However, the complexity of the systems and the need for accuracy often result in high computation times, particularly in time-based models. Such lengthy computations are not suitable for meeting the real-time requirements of the control system. Therefore, it is necessary to develop compact and efficient models that accurately represent the system's behavior.
The main challenge is to capture the complexity of the system while minimizing uncertainty in a fast and efficient computational process. This challenge is related to the need for both an enhanced physical model and a compact numerical model. The enhancement of the physical model focuses on ensuring its accuracy, while the compression of the numerical model aims to eliminate unnecessary computational overhead. These two objectives are not contradictory but rather complementary. The resulting managed models encompass both the components of the complex system and the behaviors of their environment. The intelligent supervision and management procedures act on the dynamics of the entire controlled system, including its components, as well as the sensors and actuators involved.
To address the supervision and management of EM systems, the following sections will discuss various aspects. These include the coupling models of complex systems in EM energy procedures, which involve the governing equations of EM phenomena. The intelligent supervision of EM energy procedures will also be explored, focusing on advanced control techniques. Additionally, the management of complex system models in energy procedures will be discussed, emphasizing the need for efficient and accurate models. Finally, the paper will conclude by presenting applications of complex systems in EM energy procedures, highlighting their practical implications.
3 GOVERNING EQUATIONS OF EM PHENOMENA
Regarding coupling models of CS in EM energy procedures, the main EM occurrence governing equations correspond to the Maxwell Equations[15] in their most common form that is the basic full-wave EM formulation, characterizing the EM fields involved in EM energy procedures are given by:
|
In Equations (1)-(4) H, E and B, D are the magnetic, electric, respectively fields and inductions, A and V are the magnetic vector and electric scalar potentials. J and Je are the total and source current densities, σ is the electric conductivity and ω is the radial frequency pulsation. The symbol ∇ is a vector of partial derivative operators, and its three possible inferences are gradient (product with a scalar field), divergence and curl (dot and cross products, respectively, with a vector field). The magnetic and electric behavior laws between B/H and D/E are denoted respectively by the permeability μ and the permittivity ε.
The solution of these equations, which exhibit in general nonlinear behaviors, needs numerical analysis treatments. Moreover, the geometrical complexity of system structures, which strengthens the spatial effect of material nonlinearity, imposes the use of discretized methods, as e.g. finite elements[11], for equations solutions.
4 MODELS COUPLING IN CSs IN EM ENERGY PROCEDURES
A compound system is comprised of multiple subsystems, and when these subsystems exhibit interconnected behaviors, the compound system is considered a CS. Such interconnected behaviors exhibit an interdependent nature amplified by the spatial nonlinearity and temporal behaviors of the different involved phenomena. This corresponds to the spatial and temporal multiscale character of CSs. In CSs, phenomena with interdependent nonlinear behaviors and similar time constants (TC) are strongly coupled. This means that their equations need to be solved simultaneously at a local level. On the other hand, if phenomena exhibit independent linear behaviors and have distant time constants, they are not coupled and can be solved separately through individual equations. In cases where the phenomena lie between these two situations, they are weakly coupled, and iterative solutions are generally required. Due to the nonlinear behaviors and complex geometries of the systems concerned, the equations of the different phenomena are solved using discretized methods such as finite elements. The final discretized solution involves the different local cell (element) values of the variables and parameters of the equations using matrix calculations. In the case of weakly coupled phenomena, separate matrix calculations are iteratively performed. However, for strongly coupled phenomena, a simultaneous solution is achieved using the same matrix calculation.
Regarding the case of EM procedures examples, of strongly coupled solutions could be found[16-19], and of weakly coupled solutions[20-22]. The details of the scenarios and their model implementation of these different coupled models could be found in Ref.[16-22].
Note that these coupled phenomena concern generally behaviors in EM systems but can be intrinsic to particular materials (smart materials) as e.g., magnetostrictive, electrostrictive, shape-memory and thermoelectric[23-26].
We will then consider in EM procedures, the external phenomena most often associated with EMF phenomenon, namely electrical, mechanical and thermal.
4.1 Circuits Electric Phenomenon
The next relation between the voltage (v) and current (i) can represent an external electric circuit in general:
|
In Equation (5), r is the electric resistance of the circuit, L is a linear inductance, C is a capacitance, ᴕ is a non-linear voltage drop (e.g. a semiconductor component) in the circuit and Ψ is a flux linkage relative to associated magnetic circuit. In coupled EMF system with an external electric circuit, Equation (5) should be solved with Equations (1)-(4), see[11,16,17]. In Equations (1)-(5), the electric and magnetic phenomena have TCs of relatively small and closed values and exhibit nonlinearities by ᴕ and μ. As mentioned before, these equations should be solved simultaneously in a strong coupling accomplishment.
4.2 Mechanical Phenomenon
The relation of the force and the displacement and/or its time derivatives (speed and acceleration) generally characterizes the equations involved in mechanical phenomena. The form of equations, depends on the application, see e.g. section 4.4. The mechanical phenomena equation will be solved simultaneously with Equations (1)-(4) or Equations (1)-(5) if an electric circuit is involved. The solution is, as in section 4.1, of strong coupling nature due to the closeness of mechanic, magnetic and electric TCs and involved nonlinearities; the relation between displacement and magnetic force is often nonlinear. Such coupling situations could be found in Ref.[11,18,19].
4.3 Thermal Heat Transfer Phenomenon
Thermal phenomena are generally governed by thermal heat transfer equation:
|
In Equation (6), c is the specific heat, ρ is the material density, k is thermal conductivity, T local temperature, Pd is the external heat source, corresponding in the case of EM involvement, to the power loss (dissipated) density and ∇·(k∇T) represents simple heat equation in differential form.
In case of association of the thermal phenomenon with that of EMF, the source of heat Pd in Equation (6) is determined from Equations (1)-(4) and plays the role of coupling. Its expression function of EMF depends on heated matter nature, electric conductor or dielectric. Note that the relative values of these two natures are strongly dependent on the EMF frequency, for low frequency (such that σ>>ω.ε) the conducting nature is dominant while for high frequency (such that σ<<ω.ε) the dielectric one is. The two corresponding expressions are respectively:
|
In Equations (7) and (8), E is the peak value of the electric field and ε″ is the imaginary part of the complex permittivity of the material that characterize dielectric losses.
The coupling of Equation (6) and Equations (1)-(4) is of the weak type because the thermal phenomenon TC is very high relative the EMF one. As mentioned before, the solution will be of iterative type[11,20-22,27].
4.4 Study Case Example of Coupling Strategies
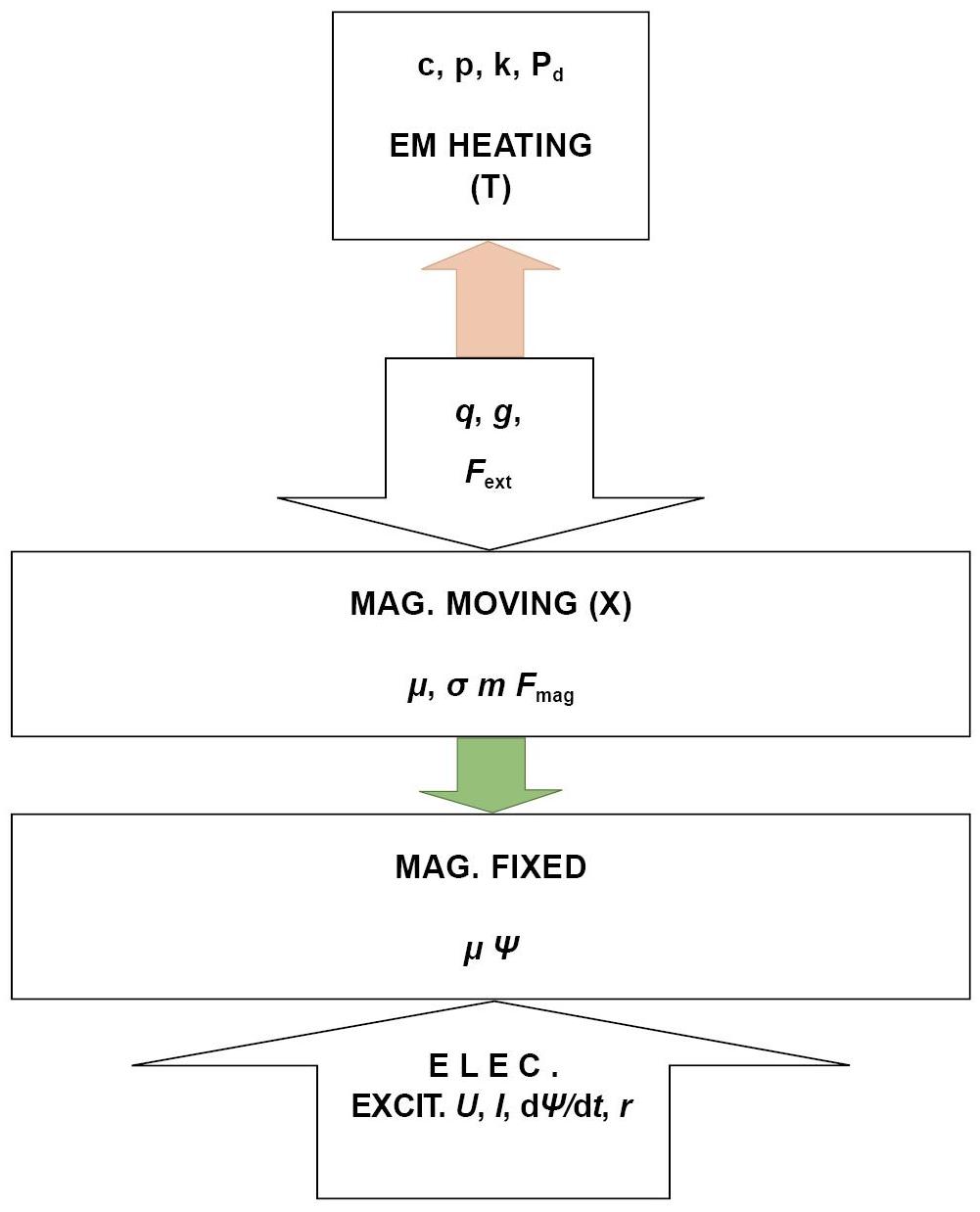
Considering a simple demonstrative example of a school case (not from the terrain) shown in Figure 1, consists of a 4 compound system comprising 3 interacting subsystems and an independent one, the whole working together as a CS. It contains two magnetic circuits; one is fixed of magnetic non-conducting material while the other is mobile of magnetic conducting material. An external electric circuit excites the fixed magnetic part, which yield a magnetic force attracting the mobile part (linked to fixed damper and spring) provoking its displacement that ending by attaching the two magnetic parts (magnet). The closure of the combined magnetic circuit triggers an independent EM heating process producing temperature rise in an object (see Figure 1).
|
Figure 1. Study case of a strong coupling (electric-magnetic-mechanic) and a weak coupling (EMF-thermic) in interconnected and independent subsystems respectively.
This corresponds to a two-phase EM procedure, where the first phase involves strongly coupled electric-magnetic-mechanical phenomena, while the second phase consists of weakly coupled EMF-thermal phenomena. In the first phase, When an external electric circuit applies a voltage “U”, the current “I” increases and the moving part is attracted by the magnetic force exerted by the fixed magnetic part. As a result, the air gap between the two magnetic parts decreases until it is completely closed, causing the current to reach a constant value. This phase primarily focuses on the interaction between the electric, magnetic, and mechanical components[28]. Once the magnetic circuit is closed, the second phase begins, involving an independent EM source that initiates a heat process. This heat process modifies the properties of the heated material. In this phase, the behavior of the heated material, including thermal conductivity and specific heat, exhibits nonlinear characteristics with respect to temperature. The spatial variations resulting from these nonlinearities differ between the two phases. The coupled phenomena observed in these electro-magneto-mechanical systems in the first phase and the EMF-thermal system in the second phase exhibit distinct nonlinear behaviors with different spatial and temporal scales, which are characteristic features of CSs.
The equations governing the first phase are Equations (1)-(4) and Equations (9) and (10) in a strong coupling, while the second phase is governed by (Equations (1)-(4), (6) and (7) or (8) ) in a weak coupling.
|
In Equation (9), X is the displacement, Fmag and Fext magnetic and external forces, m, g and q are the mass of the moving part, the damping coefficient and the stiffness of the spring, respectively. Note that Equation (10) is a particular case of Equation (5).
For more references on coupled models[11] and details of the scenarios and their model implementation of the different coupled models could be found in the different cited references[16-28].
5 SMART SUPERVISION OF EM ENERGY PROCEDURES
In the next subsections, we will discuss the supervision of energy procedures in the two cases of EM simple and CSs. A simple system denotes in general one EM device for which the automated procedure uses a simplified model for the control and the estimation of the unmeasurable parameters or variables. A CS, such as described in section 4, presents interconnected behaviors exhibiting an interdependent nature strengthened by the spatial nonlinearity degrees as well as the temporal behaviors of the different involved phenomena. The rating of such interdependence correlates the degree of complexity, which may be classified in relation to interactions[29]. According to increasing complexity, three types of connections between components or phenomena could be considered, simple, complicated and complex. The former behaves directly (without interaction), the complicated is linear and loosely coupled (buffering between components step-by-step treatments with only interactions with adjacent steps) while the complex interact with tightly coupled links (immediate connection and interaction between components - simultaneous treatments).
5.1 Supervision of EM Simple System Procedures
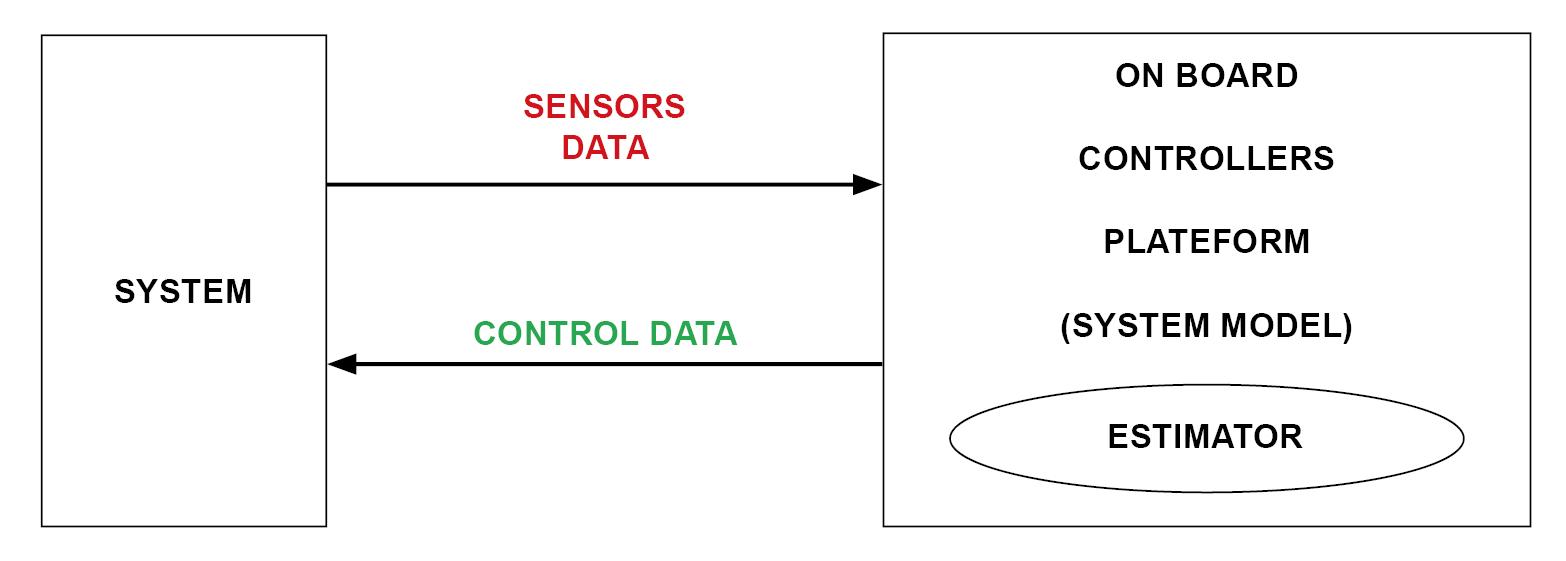
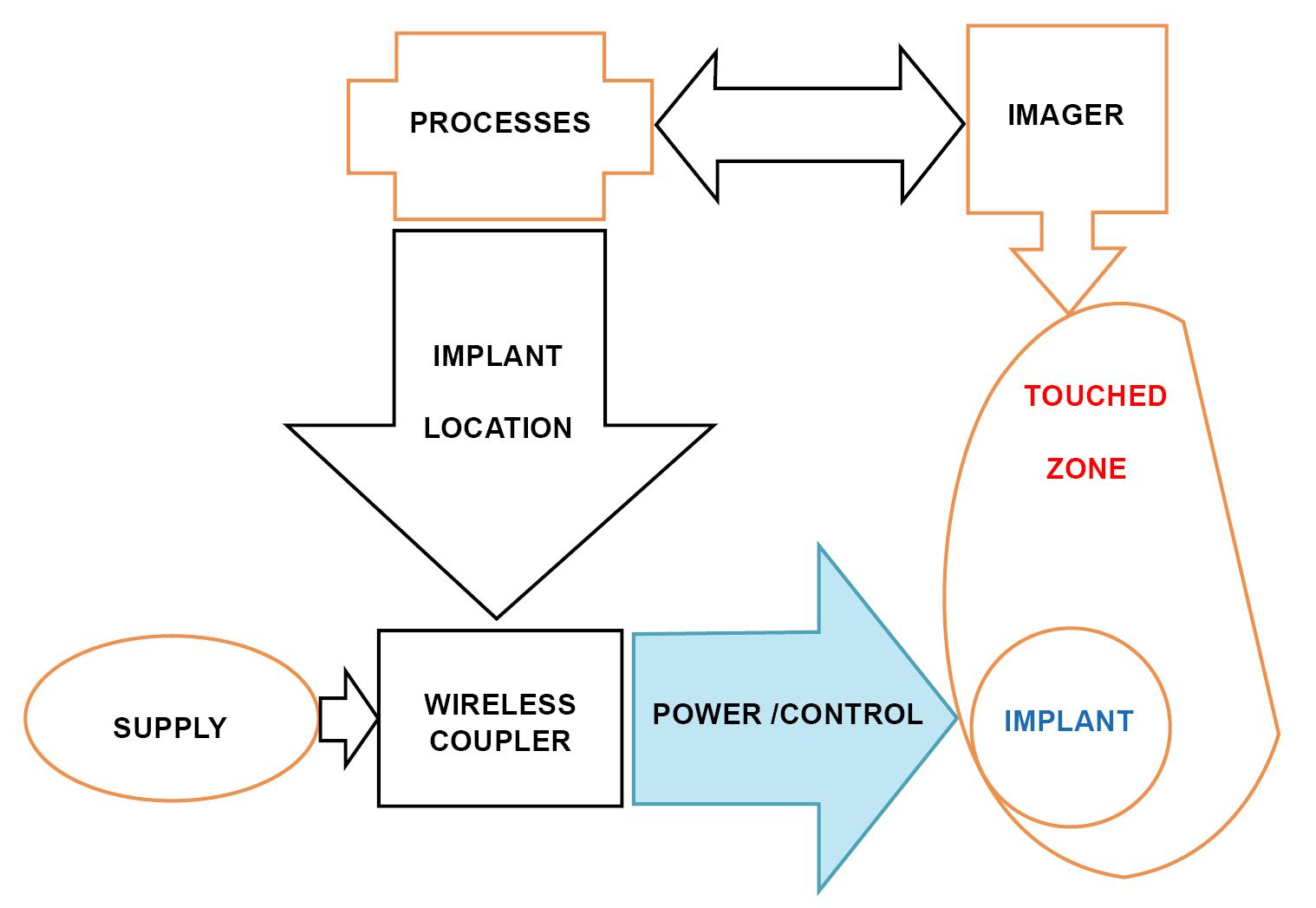
Recent energy usages related to an EM system, habitually practice automated procedures to command and enhance its performance. Such procedures manipulate as input measures flow amounts determined by sensors regarding particular functioning variables and parameters. Yet, these determinations can be challenging or unfeasible. Then, estimation can be practiced in such case. The command processes exploit the input measurements or estimations to exercise feedback orders to system control. These processes as well as estimators utilize arithmetical models typifying the actual system. The features of such model and the estimation precision act an essential role in the outing of automated procedure. As mentioned earlier, we need in general in a supervised energy procedure, a compromise between model fidelity and control swiftness. Several investigations have proposed such deal between accuracy of model and matching swiftness by fulfilling, further advanced processes, on dedicated implanted controller boards. Actually, in automated procedures, various types of state filters, controllers and observers, are available as estimators. The controller robustness is fortified by means of adaptive methodologies. Large - capacity microcontrollers know how to expand controller board strategy and software required for appraisal, which iteratively ends by matching instantly[30-37]. The general illustration of such automated procedure is shown in Figure 2. An application case of interactive autonomous image guided drug release system was illustrated in Figure 3.
|
Figure 2. Conceptual representation of iterative matching in automated system.
|
Figure 3. Interactive autonomous image guided implanted drug release iterative matching.
Besides, a more complete model technique can be adapted by reduction strategies thru precision conservation approaches[38-41].
5.2 Supervision of CS Procedures
We have mentioned before that the degree of complexity can be classified according to interactions as simple, complicated and complex. In such classification, only the two last situations are mostly involved in CSs. The difference between these situations is that complicated procedure does not alter its conduct while complex one is adaptive. Thus, the identification of the initial conditions in the first situation allows the prediction of its consequences whereas in the complex one, similar initial conditions can provoke contrasting results, depending on the interactions of the system-involved components. Complex adaptive systems can be met in numerous circumstances comprising fabricated and natural cases, e.g. human brain, which is the highest complex organization in the universe. Complexity can be related to numerous contributors, several organizational structures, or different stages that require to be supervised in a process. Complexity and CSs are the subject of numerous investigations[42-45].
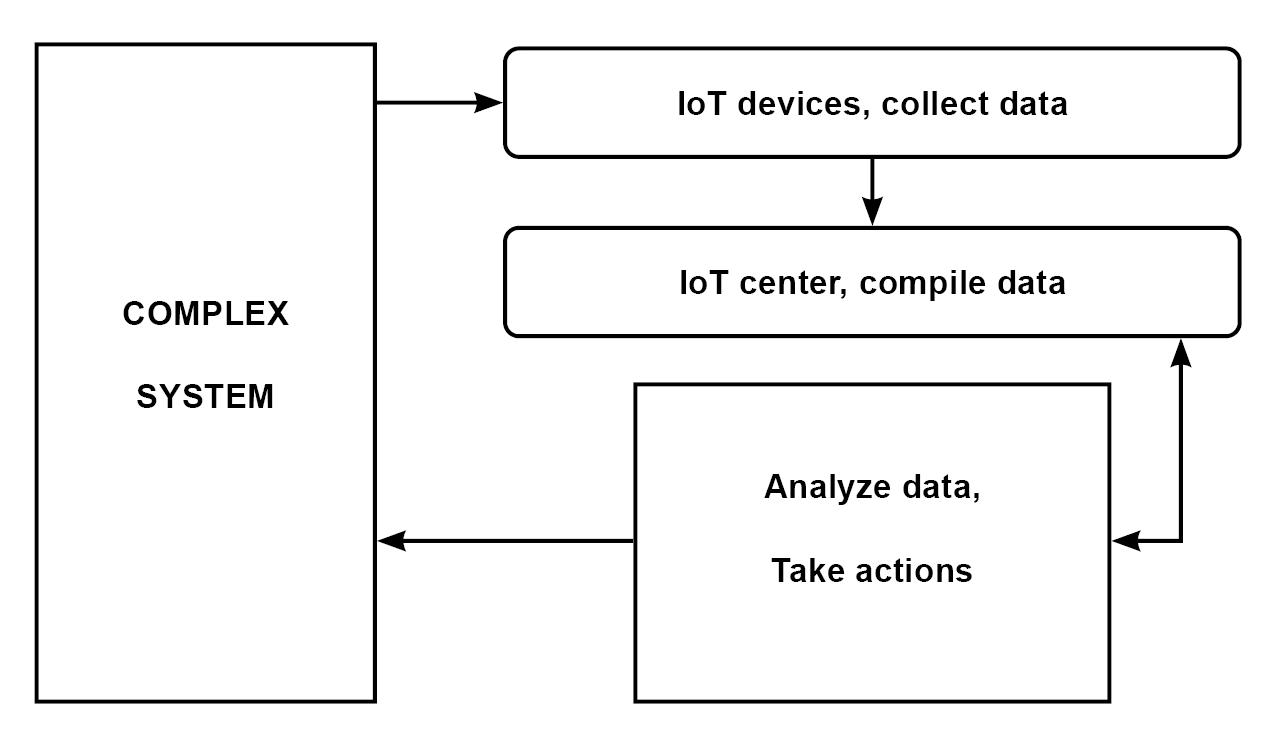
The predictableness and control facility of complex dynamical procedures are defying as shown in the last paragraph. Thus, supervision of the involved compound phenomena can be accomplished by performing the Internet of Things (IoT) that run-through strongly in the physical space through, pure immediate data assembling (see Figure 4), or computer-aided engineering (CAE) means built on achieved models implying the systems in their environments, which focuses completely on the mathematical terrain. On the other hand, it is crucial to pacify and restrain the unsuitable and unsolicited comportments that appear in these complex procedures. Achieving such, an aim requires a matching observation-model twin applied in the appropriate procedure[46].
|
Figure 4. Scheme of IoT integrated in physical space thru, immediate data assembling.
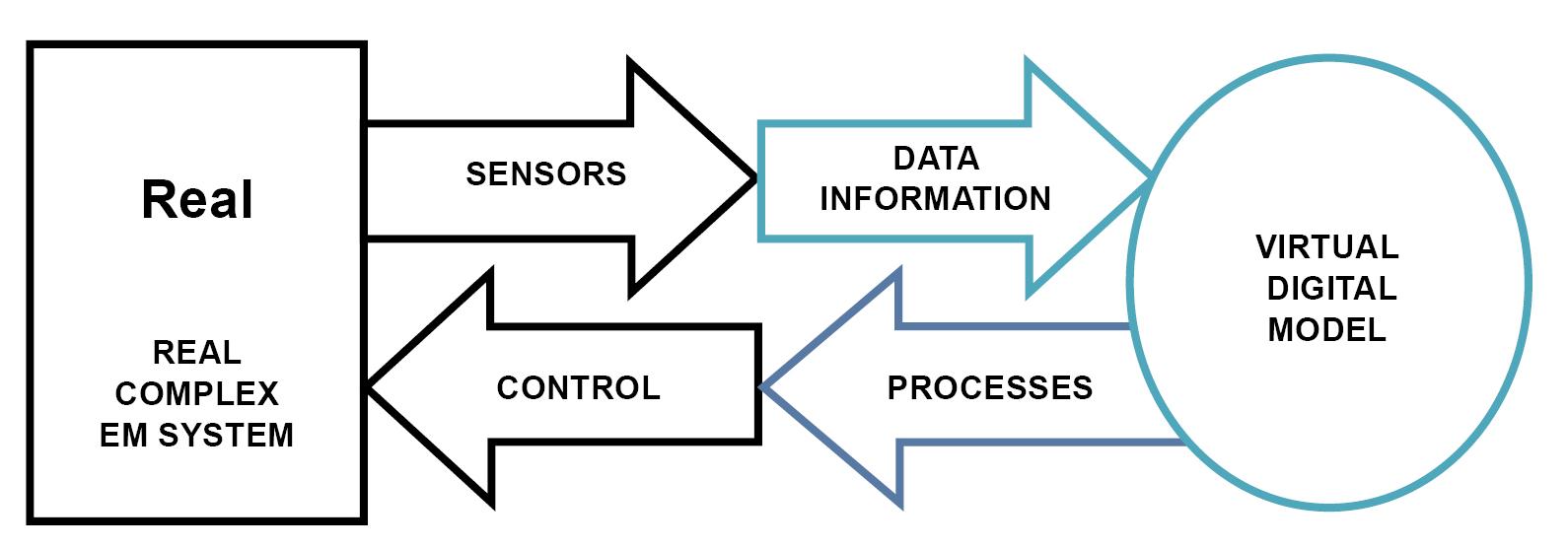
A visual representation of this matched twin concept can be depicted in Figure 5. This twin distinguishes itself from both IoT and CAE by focusing on both the physical and numerical domains. The twin requires the utilization of sensing capabilities on the observation side, computational capabilities on the model side, and data processing and control through the links connecting the two sides. On the observation side, various sensors are employed for detection and recognition of physical phenomena. On the model side, computations encompass prediction, optimization, diagnosis, simulation, and other related tasks. These computations can leverage both learned data and sensor communication to enhance their accuracy and effectiveness. The linkage between the observation and model sides is bidirectional. The observation side processes sensor measurements and provides the processed data to the model side. Conversely, the model side generates command and control data that are transmitted back to the observation side.
|
Figure 5. Schematic supervision of EM energy procedure through “observation vs. modeling matching” of its CS.
5.2.1 DT Concept
The described twin (Figure 5) reports to the DT. Grieves and Vickers[46] initially reported the notion of DT in 2002. It is characterized by a valuable two-way give-and-take amongst the mimicked and physical spheres. The three constituents of a DT are a paired observable, a real-time simulated digital component, and their measuring, treating, commanding, and pairing linkages. The physical side adjusts its comportment in harmony with the instructions formulated by the virtual side, while the last accurately reproduces the real state of the first. Hence, the DT offers an elegant relationship between the real and virtual wings[47]. Indeed, it is an online bidirectional linked pairing process, observation corrects the virtual mistake and the latter amends the data of the first. Such iterative succession guides to a more clever alliance.
The concept of DT is generally used for predictive smart maintenance, performing evaluation, fault detection, and products design. This calls different fields and innovative industrial approaches such as equipment fabricating, motorized ground transport, space and aircrafts, energy and services, healthcare and consumer products. Abundant works have been reported in literature involving different applications in these topics[48-63].
5.2.2 Matching in DT
A significant trait of DT is its capacity to reproduce the physical properties of the system online, as discussed in the previous section. However, this capability heavily relies on the mathematical methods employed, which often require significant computation time, especially in time-domain simulations. This poses a challenge for meeting the real-time requirements of the DT, particularly in the case of complex automated systems. Therefore, there is a need to develop accurate and efficient models that can be quickly executed. One potential solution is to employ model reduction techniques for systems and control. These techniques allow for the creation of compact behavioral models based on simulation data and priori knowledge of the system.
Such a solution seem to be one of the promising practices to attain the crucial objective of DT for plentiful industrial requests[38,39].
6 MANAGING OF CSs MODELS IN ENERGY PROCEDURE
Following to the analyses of sections 4 and 5 relative to respectively, EM complete accurate models of CSs and smart supervision of concerned EM energy procedures, the models employed in the latter have to be managed. These concern both the CS components and the behaviors of their environments. Indeed, the smart supervised procedure acts on the dynamics of the all-inclusive controlled involved arrangement, which comprises the system components as well as the detecting and acting devices.
6.1 Model Reduction in CSs
As discussed in section 4, complete system models are necessary to authenticate the characteristics, functioning and physical consistency of simple or CSs involved in energy procedures. The expansion in system complexity makes the models more intricate and hence amplifies the computation time. Model reduction exercises can progress a diminution in such time, while maintaining sufficient accuracy. The essence of model reduction is to keep only, the physical manifestations and quantities of significance, in a model of high sophistication, permitting a modest model that can “hopefully” be executed more efficiently. Conditional on the character of challenging and the territory of study, different model reduction methods are recommended[10-14,38-40]. In the energy procedure, in addition to the reduction of the CS model, the involved dynamics control model should as well be reduced.
6.2 Model Reduction of Procedure Dynamics Control
Model reduction practices are utilized in procedures and command sphere for the analysis of dynamical schemes and the achievement of feedback supervisions. Currently, the objective of the controller approach is to regulate the system dynamics to attain the requested comportment, e.g., smooth irregular schemes, supervise a reference trace or abolish external disturbances happening in a procedure. These management strategies are engaged in a wide-ranging diversity of troubles, involving mainly electrical and EM procedures. These utilizations assign the shared objective of functioning with procedures typified by inputs and outputs. More precisely, several actuators performing the job of inputs, affecting the procedure dynamics and several sensors acting the task of outputs are involved in such utilizations. It is central to have a correct model of such input-output comportment. However, the controller design, which is employed online, entails model order reduction. In this case, the relative model reduction techniques therefore manage to come close to the input-output behavior of a high-order model. Thus, one can use techniques that maintain the stability of the high-order model and provide a bounded error, which offers a direct assessment of the mark of the lower-order model. Many works[64-70] have been published in this field.
7 APPLICATIONS ON CS IN EM ENERGY PROCEDURES
Numerous applications on the supervision of CSs procedures have been reported in the literature as the examples discussed in section 5.1. These applications cover many topics involving energy applications. As EM energy is employed largely in many daily life domains, it is obvious that an important part of the mentioned application topics of supervision of CSs uses partially EM energy. Several examples utilizing EM energy correspond to numerous complex procedures using monitoring actuation. The involved actuators utilize EM energy. Applications examples are sustainable intelligent manufacturing, machine tools, accurate personalized medicine etc. A typical detailed example is image-guided robotics for surgical interventions and restricted delivery of implanted drugs under minimally invasive conditions. The main control in such CS concerns the actuators involved in the robot. These actuators utilize EM energy. Besides, many works[60,63] are directly related to EM energy. For the illustration of the importance of the strategies of supervision of CSs in the domain of EM energy procedures, we will consider the example of electric and intelligent vehicles and their managements. This example exhibit progresses in mathematical modeling, dynamics analysis, intelligent control, and diagnosis in vehicle engineering. This comprises diverse characteristics such as vehicle state monitoring, battery supervision arrangements, autonomous steering control, driver assist tools, electronics, electric drive structures, electric grid relates, security and health protection. These characteristics reveal a multicomponent system relating intelligent automated procedures that necessitate accurate and compact models. For example, an intelligent vehicle possesses enriched perception and reasoning. These are insured via a multicomponent system involving radar sensors, laser scanners, cameras and actuating devices that allow the automation of driving tasks such as the vehicle state monitoring and autonomous steering control.
Cases concerning principally dynamics control exist in literature[71-73]. Situations inferring energy transition and incorporation in power schemes can be attained[74-78]. Considering management of battery charging, many works[79-86] are existing. In view of renewal energy capabilities in charging control, see Ref.[87-89]. Regarding electrically powered motor diagnostics and optimization, see Ref.[90,91]. About applications of wireless charging of battery in cases of stationary, on road and underwater vehicles, see Ref.[92-96] as well as[97,98] for the control of health safety allied to these charging devices.
8 DISCUSSION
In this contribution, the evaluation and analysis of the coupling of models of CSs within the context of intelligent EM energy procedures have highlighted the importance of considering and examining such coupling to effectively manage smart supervised procedures. Several key points are discussed:
(1) Observation-Virtual Pair: The characteristics of the observation-virtual pair are discussed, with “observation” referring to sensory inspection, measurement, or maneuvering, and “virtual” indicating exploration, scientific modeling, or forecasting. When both elements of the pair are precise, they complement each other. This pairing quality can be leveraged for fine-tuning. If one element is uncertain or doubtful, it can be corroborated or rectified by the other. This mirroring approach can help address confidence issues[99]. An example is given of image-guided robotics in surgical interventions, where a physical copy of the patient is used alongside a digital procedure model, allowing for self-corrected behavior through matching and adjustment between the real and virtual sides. (2) Historical aspect of the DT concept[100]: The historical aspect of the DT concept is touched upon. It is noted that the term DT was introduced by M. Grieves in 2002, but similar concepts existed earlier. In 1993, Gelernter[101] discussed the potentials of software that exemplify a portion of reality in “Mirror Worlds”. NASA also used complex models for spacecraft security control before that[102]. The astonishing explosion of the oxygen container of the Apollo 13 mission then disturbed this in 1970[103]. After this disaster, the mission changed a number of high-reliability emulators to adapt them to the real situations of the scratched spacecraft and employed them to land securely[104]. This was probably one of the main real uses of a DT. This implied a number of fundamental characteristics of a DT, although it was not a well-known concept in 1970. (3) Complexity in characterizing CSs: The notion of complexity in characterizing CSs is discussed. It extends beyond the physical interconnectedness of different components with nonlinear behaviors, spatial and temporal scales, and dynamics. The mathematical interaction between the corresponding models is complex, and the complexity of the coupled model increases with the complexity of the real system. The coupled behavior is correlated with the control of different components of the CS due to the matching between the real CS and the virtual model. (4) Physical phenomena coupling: The coupling of physical phenomena, whether strong or weak, can be attributed to material functionality, intrinsic functioning of a system, or the interaction of different systems. Material functionality is associated with smart materials such as magnetostrictive, electrostrictive, shape-memory, and thermoelectric materials. The coupling can be strong or weak depending on the linear behavior or distant time constants. Intrinsic system functioning involves a principal governing phenomenon and secondary phenomena, which can be desired or unwanted events. The interaction of different systems characterizes CSs, and the coupled behavior is influenced by the operational control of the CS. (5) Model reduction: The concept of model reduction is discussed, emphasizing that the chosen strategy depends on the nature of the application. Model reduction aims to maintain sufficient accuracy by retaining significant physical manifestations and quantities while discarding less important details. The attributes to be preserved differ for each application, and there is no universal strategy for model reduction.
9 CONCLUSION
In this contribution, the assessment and the analysis of the coupling of models of CSs in the context of smart EM energy procedures has been achieved. The exploration of various issues related to this assessment has revealed the constant evolution of this topic.
The importance of the following questions has been highlighted: the coupling of EM phenomena with other physical phenomena, the integration of CS components, intelligent supervision of EM energy procedures, the concept of DT, pairing in automated procedures, management of CS models, optimizing matching speed in automated procedures, the notion of model reduction, and the management of electric and intelligent vehicles. These questions are relevant to various industries, the medical sector, the security field, and researchers in different domains.
Based on the discussions, the following concluding remarks can be summarized:
(1) The complexity of the real system determines the complexity of the coupled model. Complex systems require more intricate coupled models to capture their behavior accurately.
(2) Strong or weak coupling of physical phenomena can be attributed to the functionality of smart materials, the intrinsic functioning of a system, or the interaction of different components within a CS.
(3) There is no universal strategy for model reduction. The preservation of important attributes differs for each application, and the choice of model reduction strategy depends on the specific requirements and goals of the application.
(4) The practice of matching within an observation-virtual pair can be leveraged to address uncertainties in both elements of the pair. The mirroring approach allows for the correction and fine-tuning of both the real and virtual sides of the pair.
Acknowledgements
Not applicable.
Conflicts of Interest
The author declared there is no conflict of interest.
Author Contribution
Razek A contributed to the manuscript and approved the final version.
Abbreviation List
CAE, Computer-aided engineering
CS, Complex system
DT, Digital twin
EM, Electromagnetic
IoT, Internet of Things
TC, Time constants
References
[1] Monteiro J, Pedro A, Silva AJ. A Gray Code model for the encoding of grid cells in the Entorhinal Cortex. Neural Comput Appl, 2022; 34: 2287-2306.[DOI]
[2] Wang F, Tian D. On deep learning-based bias correction and downscaling of multiple climate models simulations. Clim Dynam, 2022; 59: 3451-3468.[DOI]
[3] Pendergraft JG, Carter DR, Tseng S et al. Learning from the past to advance the future: the adaptation and resilience of NASA’s Spaceflight Multiteam Systems across four eras of spaceflight. Front Psychol, 2019; 10: 1633.[DOI]
[4] Mittal V, Bhushan B. Accelerated computer vision inference with AI on the edge. 2020 IEEE 9th International Conference on Communication Systems and Network Technologies (CSNT). IEEE, 10-12 April 2020, Gwalior, India.[DOI]
[5] Amanatidis G, Aziz H, Birmpas G et al. Fair Division of Indivisible Goods: Recent Progress and Open Questions. Artif Intell, 2023; 322: 103965.[DOI]
[6] Harris K, Anagnostides I, Farina G et al. Meta-learning in games. arXiv preprint arXiv:2209.14110, 2022.[DOI]
[7] Esposito G, Terlizzi A. Governing wickedness in megaprojects: Discursive and institutional perspectives. Policy Soc, 2023; 42: 131-147.[DOI]
[8] Paluš M. Coupling in complex systems as information transfer across time scales. Philos T R Soc A, 2019; 377: 20190094.[DOI]
[9] Ali WA, Fanti MP, Roccotelli M et al. A Review of Digital Twin Technology for Electric and Autonomous Vehicles. Appl Sci, 2023; 13: 5871.[DOI]
[10] Razek A. Review of Pairing Exercises Involving a Real Event and its Virtual Model up to the Supervision of Complex Procedures. J Hum Earth Future, 2021, 2: 424-437.[DOI]
[11] Razek A. Coupled models in electromagnetic and energy conversion systems from smart theories paradigm to that of complex events: A review. Appl Sci, 2022; 12: 4675.[DOI]
[12] Benner P, Ohlberger M, Cohen A et al. Model Reduction and Approximation: Theory and Algorithms. Society for Industrial and Applied Mathematics: Philadelphia, USA, 2017.
[13] Imran M, Ahmad MI. Development of frequency weighted model order reduction techniques for discrete-time one-dimensional and two-dimensional linear systems with error bounds. IEEE Access, 2022; 10: 15096-15117.[DOI]
[14] Razek A. Strategies for managing models regarding environmental confidence and complexity involved in intelligent control of energy systems-A review. Adv Env Energies, 2023; 2.[DOI]
[15] Maxwell J C. VIII. A dynamical theory of the electromagnetic field. Philos T R Soc London, 1865; 155: 459-512.[DOI]
[16] Strohm C, Tischendorf C. Coupled Electromagnetic Field and Electric Circuit Simulation: A Waveform Relaxation Benchmark. Modeling, Simulation and Optimization of Complex Processes HPSC 2018: Proceedings of the 7th International Conference on High Performance Scientific Computing. March 19-23, 2018. Hanoi, Vietnam.[DOI]
[17] Piriou F, Razek A. A non-linear coupled 3D model for magnetic field and electric circuit equations. IEEE T Magn, 1992; 28: 1295-1298.[DOI]
[18] Henrotte F, Nicolet A, Hedia H et al. Modelling of electromechanical relays taking into account movement and electric circuits. IEEE T Magn, 1994; 30: 3236-3239.[DOI]
[19] Ren Z, Razek A. A coupled electromagnetic-mechanical model for thin conductive plate deflection analysis. IEEE T Magn, 1990; 26: 1650-1652.[DOI]
[20] Bay F, Labbé V, Favennec Y et al. A numerical model for induction heating processes coupling electromagnetism and thermomechanics. Int J Numer Meth Eng, 2003; 58: 839-867.[DOI]
[21] Sekkak A, Pichon L, Razek A. 3-D FEM magneto-thermal analysis in microwave ovens. IEEE T Magn, 1994; 30: 3347-3350.[DOI]
[22] Kopyt P, Celuch M. Coupled electromagnetic-thermodynamic simulations of microwave heating problems using the FDTD algorithm. J Microwave Power Ee, 2006; 41: 18-29.[DOI]
[23] Hariri H, Bernard Y, Razek A. 2-D traveling wave driven piezoelectric plate robot for planar motion. IEEE T Magn, 2018; 23: 242-251.[DOI]
[24] Rios S A, Fleming A J, Yong Y K. Miniature resonant ambulatory robot. IEEE Robot Autom Let, 2016; 2: 337-343.[DOI]
[25] Besbes M, Ren Z, Razek A. A generalized finite element model of magnetostriction phenomena. IEEE T Magn, 2001; 37: 3324-3328.[DOI]
[26] Bottauscio O, Roccato PE, Zucca M. Modeling the dynamic behavior of magnetostrictive actuators. IEEE T Magn, 2010; 46: 3022-3028.[DOI]
[27] Razek A. Thermal effects of electromagnetic origin from heating processes to biological disturbances due to field exposure-A review. Therm Sci Eng, 2023; 6: 20-33.[DOI]
[28] Ren Z, Razek A. A strong coupled model for analyzing dynamic behaviors of non-linear electromechanical systems. IEEE T Magn, 1994; 30: 3252-3255.[DOI]
[29] Perrow C. Normal Accidents: Living with High Risk Technologies - Updated Edition. Princeton University Press: New Jersey, USA, 2011.[DOI]
[30] Xu D, Wang B, Zhang G et al. A review of sensorless control methods for AC motor drives. CES T Elec Mach Syst, 2018; 2: 104-115.[DOI]
[31] Soto GG, Mendes E, Razek A. Reduced-order observers for rotor flux, rotor resistance and speed estimation for vector controlled induction motor drives using the extended Kalman filter technique. IEE P-Electr Power App, 1999; 146: 282-288.[DOI]
[32] Alonge F, D'Ippolito F, Sferlazza A. Sensorless control of induction-motor drive based on robust Kalman filter and adaptive speed estimation. IEEE T Ind Electron, 2013; 61: 1444-1453.[DOI]
[33] El Moucary C, Mendes E, Razek A. Decoupled direct control for PWM inverter-fed induction motor drives. IEEE T Ind Appl, 2002; 38: 1307-1315.[DOI]
[34] Holtz J, Quan J. Drift-and parameter-compensated flux estimator for persistent zero-stator-frequency operation of sensorless-controlled induction motors. IEEE T Ind Appl, 2003; 39: 1052-1060.[DOI]
[35] Ortega R, Aranovskiy S, Pyrkin AA et al. New results on parameter estimation via dynamic regressor extension and mixing: Continuous and discrete-time cases. IEEE T Automat Contr, 2020; 66: 2265-2272.[DOI]
[36] Mendes E, Baba A, Razek A. Losses minimization of a field oriented controlled induction machine. IEEE Conference Publication, 1995; 412: 310-314.[DOI]
[37] Razek A. Towards an image-guided restricted drug release in friendly implanted therapeutics. Eur Phys J-Appl Phys, 2018; 82: 31401.[DOI]
[38] Guo Z, Yan S, Xu X et al. Twin-model based on model order reduction for rotating motors. IEEE T Magn, 2022; 58: 1-4.[DOI]
[39] Besselink B, Tabak U, Lutowska A et al. A comparison of model reduction techniques from structural dynamics, numerical mathematics and systems and control. J Sound Vib, 2013; 332: 4403-4422.[DOI]
[40] Tol HJ, de Visser CC, Kotsonis M. Model reduction of parabolic PDEs using multivariate splines. Int J Con, 2019; 92: 175-190.[DOI]
[41] Nunes AS, Dular P, Chadebec O et al. Subproblems applied to a 3-D magnetostatic facet FEM formulation. IEEE T Magn, 2018; 54: 1-9.[DOI]
[42] Tolk A. Simulation-Based Optimization: Implications of Complex Adaptive Systems and Deep Uncertainty. Information, 2022; 13: 469.[DOI]
[43] Wen J, Gabrys B, Musial K. Towards digital twin oriented modelling of complex networked systems and their dynamics: a comprehensive survey. IEEE Access, 2022.[DOI]
[44] Oliveira Monteiro LM, Saraiva JP, Brizola Toscan R et al. PredicTF: prediction of bacterial transcription factors in complex microbial communities using deep learning. Environ Microbiome, 2022; 17: 1-11.[DOI]
[45] Helbing D, Sánchez-Vaquerizo JA. Digital twins: potentials, ethical issues and limitations. In: Handbook on the politics and governance of Big Data and Artificial Intelligence. Edward Elgar Publishing: Chottham College, UK, 2023; 64-104.
[46] Grieves M, Vickers J. Digital twin: Mitigating unpredictable, undesirable emergent behavior in complex systems. In: Transdisciplinary perspectives on complex systems. Springer, Cham. 2017; 85-113.[DOI]
[47] Tao F, Sui F, Liu A et al. Digital twin-driven product design framework. Int J Prod Res, 2019; 57: 3935-3953.[DOI]
[48] He B, Bai KJ. Digital twin-based sustainable intelligent manufacturing: A review. Adv Manuf, 2021; 9: 1-21.[DOI]
[49] Cai Y, Starly B, Cohen P et al. Sensor data and information fusion to construct digital-twins virtual machine tools for cyber-physical manufacturing. Procedia Manuf, 2017; 10: 1031-1042.[DOI]
[50] Selçuk ŞY, Ünal P, Albayrak Ö et al. A workflow for synthetic data generation and predictive maintenance for vibration data. Information, 2021; 12: 386.[DOI]
[51] Jimenez JJM, Schwartz S, Vingerhoeds R et al. Towards multi-model approaches to predictive maintenance: A systematic literature survey on diagnostics and prognostics. J Manuf Syst, 2020; 56: 539-557.[DOI]
[52] Nacchia M, Fruggiero F, Lambiase A et al. A systematic mapping of the advancing use of machine learning techniques for predictive maintenance in the manufacturing sector. Appl Sci, 2021; 11: 2546.[DOI]
[53] Liu Z, Meyendorf N, Mrad N. The role of data fusion in predictive maintenance using digital twin. AIP conference proceedings. AIP Publishing, 2018, 1949.[DOI]
[54] Liu Y, Zhang L, Yang Y et al. A novel cloud-based framework for the elderly healthcare services using digital twin. IEEE access, 2019; 7: 49088-49101.[DOI]
[55] Kamel Boulos MN, Zhang P. Digital twins: from personalised medicine to precision public health. J Pers Med, 2021; 11: 745.[DOI]
[56] Holmes D, Papathanasaki M, Maglaras L et al. Digital Twins and Cyber Security–solution or challenge? 2021 6th South-East Europe Design Automation, Computer Engineering, Computer Networks and Social Media Conference (SEEDA-CECNSM). IEEE, 2021: 1-8.[DOI]
[57] Gehrmann C, Gunnarsson M. A digital twin based industrial automation and control system security architecture. IEEE T Ind Inform, 2019; 16: 669-680.[DOI]
[58] Boschert S, Rosen R. Digital twin—the simulation aspect. In: Mechatronic futures: Challenges and solutions for mechatronic systems and their designers. Springer, Cham. 2016: 59-74.[DOI]
[59] Shirowzhan S, Tan W, Sepasgozar SME. Digital twin and CyberGIS for improving connectivity and measuring the impact of infrastructure construction planning in smart cities. ISPRS Int J Geo-Inf, 2020; 9: 240.[DOI]
[60] Bhatti G, Mohan H, Singh RR. Towards the future of smart electric vehicles: Digital twin technology. Renew Sust Energ Rev, 2021; 141: 110801.[DOI]
[61] Chen X, Min X, Li N et al. Dynamic safety measurement-control technology for intelligent connected vehicles based on digital twin system. Vibroeng Procedia, 2021; 37: 78-85.[DOI]
[62] Liu S, Wang XV, Wang L. Digital twin-enabled advance execution for human-robot collaborative assembly. CIRP Annals, 2022; 71: 25-28.[DOI]
[63] Brosinsky C, Westermann D, Krebs R. Recent and prospective developments in power system control centers: Adapting the digital twin technology for application in power system control centers. 2018 IEEE International Energy Conference (ENERGYCON). IEEE, 3-7 June 2018, Limassol, Cyprus.[DOI]
[64] Enns DF. Model reduction with balanced realizations: An error bound and a frequency weighted generalization. The 23rd IEEE conference on decision and control. IEEE, 12-14 December 1984, Las Vegas, NV, USA.[DOI]
[65] Glover K. All optimal Hankel-norm approximations of linear multivariable systems and their L,∞-error bounds. Int J Con, 1984; 39: 1115-1193.[DOI]
[66] Moore B. Principal component analysis in linear systems: Controllability, observability, and model reduction. IEEE T Automat Contr, 1981; 26: 17-32.[DOI]
[67] Sarkar A, Scherpen JMA. Extended differential balancing for nonlinear dynamical systems. IEEE Contr Syst Lett, 2022; 6: 3170-3175.[DOI]
[68] Gao Y, Liu J, Li M, et al. Design of Asynchronous Motor Controller Based on Controlled Lagrangians Method. Math Probl Eng, 2022, 2022.[DOI]
[69] Borja P, Scherpen JMA, Fujimoto K. Extended balancing of continuous LTI systems: a structure-preserving approach. IEEE T Automat Contr, 2021; 68: 257-271.[DOI]
[70] Nie X, Min C, Pan Y et al. Deep-neural-network-based modelling of longitudinal-lateral dynamics to predict the vehicle states for autonomous driving. Sensors, 2022; 22: 2013.[DOI]
[71] Farroni F, Sakhnevych A. Tire multiphysical modeling for the analysis of thermal and wear sensitivity on vehicle objective dynamics and racing performances. Simul Model Pract Th, 2022; 117: 102517.[DOI]
[72] Mosconi L, Farroni F, Sakhnevych A et al. Adaptive vehicle dynamics state estimator for onboard automotive applications and performance analysis. Vehicle Syst Dyn, 2023; 61: 3244-3268.[DOI]
[73] Hulagu S, Celikoglu HB. An electric vehicle routing problem with intermediate nodes for shuttle fleets. IEEE T Intell Transp, 2020; 23: 1223-1235.[DOI]
[74] Bellocchi S, Klöckner K, Manno M et al. On the role of electric vehicles towards low-carbon energy systems: Italy and Germany in comparison. Appl Energ, 2019; 255: 113848.[DOI]
[75] Qiu D, Wang Y, Zhang T et al. Hybrid multiagent reinforcement learning for electric vehicle resilience control towards a low-carbon transition. IEEE T Ind Inform, 2022; 18: 8258-8269.[DOI]
[76] Shaukat N, Ali SM, Mehmood CA et al. A survey on consumers empowerment, communication technologies, and renewable generation penetration within Smart Grid. Renew Sust Energ Rev, 2018; 81: 1453-1475.[DOI]
[77] Yang Z, Li K, Foley A. Computational scheduling methods for integrating plug-in electric vehicles with power systems: A review. Renew Sust Energ Rev, 2015; 51: 396-416.[DOI]
[78] Venegas FG, Petit M, Perez Y. Active integration of electric vehicles into distribution grids: Barriers and frameworks for flexibility services. Renew Sust Energ Rev, 2021; 145: 111060.[DOI]
[79] Yan L, Chen X, Chen Y et al. A cooperative charging control strategy for electric vehicles based on multiagent deep reinforcement learning. IEEE T Ind Inform, 2022; 18: 8765-8775.[DOI]
[80] Sadeghianpourhamami N, Deleu J, Develder C. Definition and evaluation of model-free coordination of electrical vehicle charging with reinforcement learning. IEEE T Smart Grid, 2019; 11: 203-214.[DOI]
[81] Jin J, Xu Y. Optimal policy characterization enhanced actor-critic approach for electric vehicle charging scheduling in a power distribution network. IEEE T Smart Grid, 2020; 12: 1416-1428.[DOI]
[82] Zhang F, Yang Q, An D. CDDPG: A deep-reinforcement-learning-based approach for electric vehicle charging control. IEEE Internet Things, 2020; 8: 3075-3087.[DOI]
[83] Wang R, Chen Z, Xing Q et al. A modified rainbow-based deep reinforcement learning method for optimal scheduling of charging station. Sustainability, 2022; 14: 1884.[DOI]
[84] Wang S, Bi S, Zhang YA. Reinforcement learning for real-time pricing and scheduling control in EV charging stations. IEEE T Ind Inform, 2019; 17: 849-859.[DOI]
[85] Zhao Z, Lee CKM. Dynamic pricing for EV charging stations: A deep reinforcement learning approach. IEEE T Transp Electr, 2021; 8: 2456-2468.[DOI]
[86] Xu P, Zhang J, Gao T et al. Real-time fast charging station recommendation for electric vehicles in coupled power-transportation networks: A graph reinforcement learning method. Int J Elec Power, 2022; 141: 108030.[DOI]
[87] Qiu D, Wang Y, Hua W et al. Reinforcement learning for electric vehicle applications in power systems: A critical review. Renew Sust Energ Rev, 2023; 173: 113052.[DOI]
[88] Dorokhova M, Martinson Y, Ballif C et al. Deep reinforcement learning control of electric vehicle charging in the presence of photovoltaic generation. Appl Energ, 2021; 301: 117504.[DOI]
[89] Yang A, Sun H, Zhang X. Deep Reinforcement Learning Strategy for Electric Vehicle Charging Considering Wind Power Fluctuation. J Eng Sci Technol Rev, 2021; 14: 103-110.[DOI]
[90] Sarigiannidis AG, Beniakar ME, Kladas AG. Fast adaptive evolutionary PM traction motor optimization based on electric vehicle drive cycle. IEEE T Veh Technol, 2016; 66: 5762-5774.[DOI]
[91] Naseri F, Schaltz E, Lu K et al. Real‐time open‐switch fault diagnosis in automotive permanent magnet synchronous motor drives based on Kalman filter. IET Power Electron, 2020; 13: 2450-2460.[DOI]
[92] Razek A. Review of contactless energy transfer concept applied to inductive power transfer systems in electric vehicles. Appl Sci, 2021; 11: 3221.[DOI]
[93] Ibrahim M, Pichon L, Bernard L et al. Advanced modeling of a 2-kW series-series resonating inductive charger for real electric vehicle. IEEE T Veh Technol, 2014; 64: 421-430.[DOI]
[94] Cirimele V, Torchio R, Villa JL et al. Uncertainty quantification for SAE J2954 compliant static wireless charge components. IEEE Access, 2020; 8: 171489-171501.[DOI]
[95] Cirimele V, Diana M, Bellotti F et al. The fabric ICT platform for managing wireless dynamic charging road lanes. IEEE T Veh Technol, 2020; 69: 2501-2512.[DOI]
[96] Zhang B, Wang X, Lu C et al. A wireless power transfer system for an autonomous underwater vehicle based on lightweight universal variable ring‐shaped magnetic coupling. Int J Circ Theor App, 2023; 51: 2654-2673.[DOI]
[97] Ding PP, Bernard L, Pichon L et al. Evaluation of electromagnetic fields in human body exposed to wireless inductive charging system. IEEE T Magn, 2014; 50: 1037-1040.[DOI]
[98] Asa E, Mohammad M, Onar OC et al. Review of safety and exposure limits of electromagnetic fields (EMF) in wireless electric vehicle charging (WEVC) applications. 2020 IEEE Transportation Electrification Conference & Expo (ITEC). IEEE, 23-26 June 2020, Chicago, IL, USA.[DOI]
[99] Hamilton F, Lloyd AL, Flores KB. Hybrid modeling and prediction of dynamical systems. PLoS Comput Biol, 2017; 13: e1005655.[DOI]
[100] Neethirajan S, Kemp B. Digital twins in livestock farming. Animals, 2021; 11: 1008.[DOI]
[101] Gelernter D. Mirror worlds: Or the day software puts the universe in a shoebox... How it will happen and what it will mean. Oxford University Press: Oxford, UK, 1993.
[102] Tao F, Qi Q. Make more digital twins. Nature, 2019; 573: 490-491.[DOI]
[103] Boy GA. Human-systems integration: from virtual to tangible. CRC Press: Florida, USA, 2020.[DOI]
[104] Zhuang C, Miao T, Liu J et al. The connotation of digital twin, and the construction and application method of shop-floor digital twin. Robot Cim-Int Manuf, 2021; 68: 102075.[DOI]
Copyright © 2024 The Author(s). This open-access article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, sharing, adaptation, distribution, and reproduction in any medium, provided the original work is properly cited.

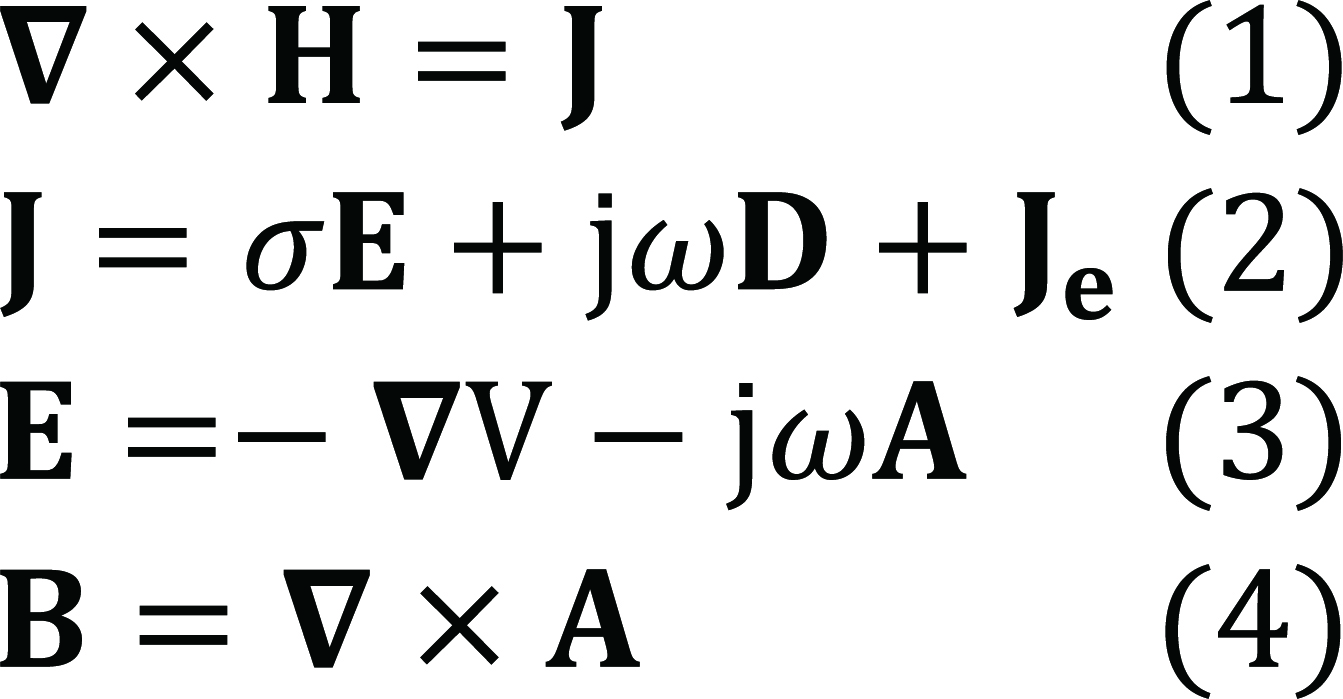



 Copyright ©
Copyright ©