Understanding Ferroelectric Phase Transitions and Domain Switching by Phase-field Modeling

 

Shiyu Tang1,2, Houbing Huang1,2*

 

1School of Materials Science and Engineering, Beijing Institute of Technology, Beijing, China

2Advanced Research Institute of Multidisciplinary Science, Beijing Institute of Technology, Beijing, China

 

*Correspondence to: Houbing Huang, PhD, Professor, School of Materials Science and Engineering, Beijing Institute of Technology, No. 5 Zhongguancun Street, Beijing, 100081, China; Email: hbhuang@bit.edu.cn

 

DOI: 10.53964/id.2024022

 

Abstract

Ferroelectric materials, characterized by their high dielectric constants, piezoelectricity, and pyroelectricity, find numerous applications in electronic products such as computer memory, highly sensitive sensors, and sonar devices. Additionally, they hold potential applications in fields like solid-state refrigeration, with their performance often closely linked to their microstructural evolution, including phase transitions and domain switching. Phase-field methods serve as highly advantageous tools for exploring, revealing, and predicting mesoscale ferroelectric domain evolution. Within ferroelectric phase-field models, diverse types of domain structures of ferroelectric materials, such as bulk single crystals and thin films, can be simulated by setting different mechanical and electrical boundary conditions. Various types of ferroelectric phase transitions can also be studied by setting conditions in the models such as temperature variations and the application of external electric fields. Furthermore, by applying external electrical or mechanical stimuli in the phase-field models, behaviors such as ferroelectric domain switching can be observed. Here we first outline the fundamental framework of phase-field models, followed by a comprehensive overview of various phase transitions in ferroelectric materials, including ferroelectric-to-paraelectric and antiferroelectric-to-ferroelectric transitions. Additionally, the review summarizes how phase-field models facilitate the induction of ferroelectric domain switching through various experimental stimuli, including electric fields and mechanical fields. This review concludes by summarizing and prospecting potential new applications of the phase-field method in the study of ferroelectric phase transitions and domain switching.

 

Keywords: ferroelectric materials, phase transitions, domain switching, phase-field simulations

 

1 INTRODUCTION

Ferroelectric materials are a class of materials that exhibit spontaneous polarization, which can be reversed under an external field. These materials undergo phase transitions from a high-temperature paraelectric state to a ferroelectric phase with polarization, as well as transitions between different ferroelectric phases, with the paraelectric-to-ferroelectric transition temperature known as the Curie temperature (TC). In ferroelectric crystals, when cooled from the high-temperature paraelectric phase without applying any external field, the ferroelectric phase can adopt multiple crystallographic orientations with equal energy, resulting in the formation of ferroelectric domains. These domains can be reversed by an external electric field. In most intrinsic ferroelectric materials, polarization is coupled with lattice degrees of freedom and can be reversed by applying a mechanical field. The macroscopic manifestation of domain switching in ferroelectric materials includes the polarization-electric field (P-E) loop associated with electric field-induced domain switching and the strain-electric field loop associated with mechanical field-induced domain switching. The ability of ferroelectric materials to undergo domain switching and exhibit lattice-coupled polarization characteristics makes them suitable for various applications, including Ferroelectric Random-Access Memories[1], actuators, sensors, and transducers[2]. The performance of these devices depends on various properties of the ferroelectric materials such as coercive field, remnant polarization, and electromechanical coupling coefficient, which are closely related to the domain switching behavior in ferroelectric materials. Therefore, studying domain switching in ferroelectric materials is crucial and necessary.

 

Among various computational methods, phase-field simulation has emerged as a powerful approach for studying the evolution of microstructures and domain configurations in ferroelectric materials. Unlike traditional atomistic simulations, which are limited to small length and time scales, phase-field simulations capture mesoscopic phenomena over larger spatial and temporal domains. By treating polarization as a spatially varying order parameter, phase-field models enable the investigation of domain nucleation, growth, and kinetics under diverse external conditions, including temperature variations, mechanical loading, and electric fields (Figure 1).

 

Figure 1. Schematic and examples of phase field simulations of ferroelectric phase transitions and domain switching[3-6]. The upper left panel reproduced from Ref.[3] with permission from Elsevier. The lower left panel reproduced from Ref.[4] with permission from ACS publications. The upper right panel reproduced from Ref.[5] with permission from Elsevier. The lower right panel reproduced from Ref.[6] with permission from OAE Publishing Inc.

 

The importance of phase-field simulation in the realm of ferroelectric materials stems from its ability to bridge the gap between theoretical predictions and experimental observations. Through computational modeling, researchers can explore a wide range of parameters and scenarios that are difficult or impractical to achieve experimentally. Moreover, phase-field simulations provide valuable insights into the underlying mechanisms driving domain dynamics and phase transitions, unraveling intricate details that may elude experimental characterization techniques alone.

 

In this comprehensive review, we delve into the pivotal role of phase-field simulation in unraveling the complexities of ferroelectric materials. We explore the fundamental principles underlying phase-field modeling and its application to elucidate the mechanisms governing phase transitions and domain dynamics in ferroelectrics. Through a systematic examination of recent advancements and key findings, we aim to provide a comprehensive overview of the state-of-the-art in this burgeoning field. By synthesizing insights from theoretical, computational, and experimental studies, we endeavor to shed light on the prospects and challenges in harnessing the potential of ferroelectric materials for next-generation technologies.

 

2 PHASE-FIELD METHOD

The phase-field method is a density-based computational technique at the mesoscale for modeling and predicting the temporal and spatial evolution of materials microstructures as well as their responses to external fields and thus properties. The phase-field simulation of ferroelectric material relies on the Ginzburg-Landau-Devonshire theory. By solving the phase-field equation, we can acquire the temporal and spatial microscopic topography of the system under study. The domain structure generally employs spontaneous polarization P as the order parameter. The energy minimization principle was applied to solve the time-dependent Ginzburg-Landau equation and mechanical equilibrium equation.

 

 

Here, L is a kinetic coefficient related to domain wall mobility, F is the total free energy of the system, is the thermodynamic driving force for polarization evolution, σij is the stress tensor, and r and t are the spatial coordinate and time, respectively. The total free energy of a bulk system can be defined as follows

 

 

Here, the total free energy Ftotal is composed of bulk energy Fbulk(P), gradient energy Fgrad(P), elastic energy Felas(P, ε), and electrical energy Felec(P, E), where E is the external electric field.

 

The bulk free energy is expressed as a six-order polynomial expansion as follows:

 

 

where αi, αij, αijk denote the Landau parameters that can be obtained from the experiment.

 

The elastic energy density can be expressed as

 

 

where Cijkl is the elastic stiffness tensor, εij is the total strain and is the spontaneous strain during the phase transformation. The spontaneous strain is related to the polarization by the electro-strictive coefficients =QijklPkPl, where Qijkl is the electro-strictive coefficient.

 

The gradient energy density is written as

 

 

where Gijkl is the gradient coefficient and Pi,j denotes the derivation of the ith component of the polarization vector Pi, with respect to the jth coordinate. In three-dimensional space, i, j=1, 2, 3.

 

The electrical energy expression can be written as

 

 

where E is the total electric field, which can be described as, E=Eappl+Edip, where Eappl is the applied electric field, Edip is the dipole-dipole interaction field.

 

There are several methods for solving phase field equations, such as spectral methods[7], finite element methods[8,9], and finite difference methods[10]. Generally, spectral methods offer the highest computational efficiency, especially when materials (such as bulk situations) can be assumed to have periodic boundary conditions. Meanwhile, through techniques like superposition and perturbation iteration, spectral methods can also be applied to situations with non-periodic boundary conditions, such as thin films. Finite element methods discretize the phase field equations in real space and perform explicit time integration. While their computational efficiency is far lower than spectral methods, they can be applied to models with complex geometric shapes due to the greater freedom they provide in selecting boundary conditions. The phase-field simulation method can simulate the domain structure of ferroelectric materials on a mesoscopic scale. In addition, through phase-field simulation, one can also intuitively see the changes in the domain structure of ferroelectric materials with different compositions, sizes, and shapes, and simulate the influence of external stimuli such as strain on the domain structure, thereby adjusting the ferroelectric properties through the change of polarization.

 

3 PHASE TRANSITION

Ferroelectric phase transition is a crucial topic in the field of ferroelectrics. When a ferroelectric material undergoes a phase transition, its polarization state often undergoes significant changes. These alterations not only determine the material’s electrical properties but also affect its mechanical, optical, and thermal properties. Consequently, ferroelectric phase transitions play a central role in numerous application areas such as storage devices, sensors, actuators, and refrigeration technologies. However, due to the complexity of phase transition processes, traditional experimental methods often struggle to provide a comprehensive understanding of the microscopic mechanisms involved. Phase-field simulations offer a solution by simulating the evolution of ferroelectric material microstructures at the mesoscale, capturing various phase transition processes (ferroelectric-to-paraelectric, ferroelectric-to-ferroelectric, ferroelectric-to-antiferroelectric phase transitions) along with the evolution of polarization and domain structure changes. Thus, phase-field simulations can reveal the microscopic mechanisms underlying phase transitions, predict the macroscopic properties of materials, and complement experimental limitations. In this chapter, we will explore the advancements in the application of phase-field simulations in the study of ferroelectric phase transitions, focusing on two types of phase transitions: ferroelectric-to-paraelectric and ferroelectric-to-antiferroelectric transitions. We will discuss how phase-field simulations reveal key factors involved in these phase transition processes and how these findings contribute to the understanding of controlling the properties of ferroelectric materials, thereby driving advancements in related application technologies. By comprehensively analyzing existing research findings, our aim is to provide insights for future research directions and application developments.

 

3.1 Temperature-induced Phase Transition

One of the most important properties of ferroelectric materials is the Tc, at which a phase transition from a ferroelectric phase to a paraelectric phase occurs. Generally, ferroelectric materials exhibit spontaneous polarization below Tc, leading to a series of unique properties such as piezoelectricity, electro-optic effects, and pyroelectricity. As the material approaches the Tc, significant changes occur in its dielectric, thermal, and mechanical properties, which are essential for understanding the material's fundamental physics and optimizing its performance. Among these properties, pyroelectricity is one of the most promising performances of ferroelectric materials in the ferroelectric-to-paraelectric phase transition. The electrocaloric effect (ECE) refers to the phenomenon where the polarization state of a ferroelectric material changes due to the application or removal of an external electric field, resulting in a change in material temperature. When a ferroelectric material changes its electric field under adiabatic conditions, the exchange of internal energy with the surroundings mainly occurs through entropy changes, leading to temperature variations in the material system. The ECE provides an efficient and environmentally friendly alternative for solid-state refrigeration technology, avoiding the use of chemical refrigerants in traditional gas compression refrigeration techniques and thus helping to reduce environmental impact. It is challenging to observe the polarization distribution of materials during the application of an electric field experimentally. Therefore, phase-field simulation methods can simulate the domain structure of ferroelectric materials at the mesoscale, enabling the adjustment of material domain structures to control the performance of ECEs.

 

The ECE is closely related to the microstructure of ferroelectric materials. By manipulating the microstructural composition, the ferroelectric properties of materials, such as polarization intensity and phase transition temperature, can be altered, thereby affecting the ECE performance. Specifically, microstructural composition can be controlled through methods such as element doping, formation of multilayer structures, and material compositing. In perovskite materials, introducing other elements into the A and/or B sites to form solid solutions can achieve excellent ECE performance under specific compositions. Firstly, by adjusting the proportion of doping elements, the phase transition temperature can be shifted into the room temperature (RT) range. Secondly, element doping can induce new phases or create diffuse phase transitions, widening the working temperature range of the material. This strategy has been implemented in lead titanate and barium titanate. Qiu et al.[11] obtained significant RT ECE by thermodynamic calculations through Sr2+ doping in the A site of lead titanate. Doping Zr4+ into the B site of lead titanate is a more common practice. Experimentally, a high adiabatic temperature change of up to 12K near the Tc has been achieved on PbZr0.95Ti0.05O3 thin films[12], generating widespread interest. Many researchers have studied the ECE of different compositions of PZT through thermodynamic calculations and constructing phase-field models[13-18].

 

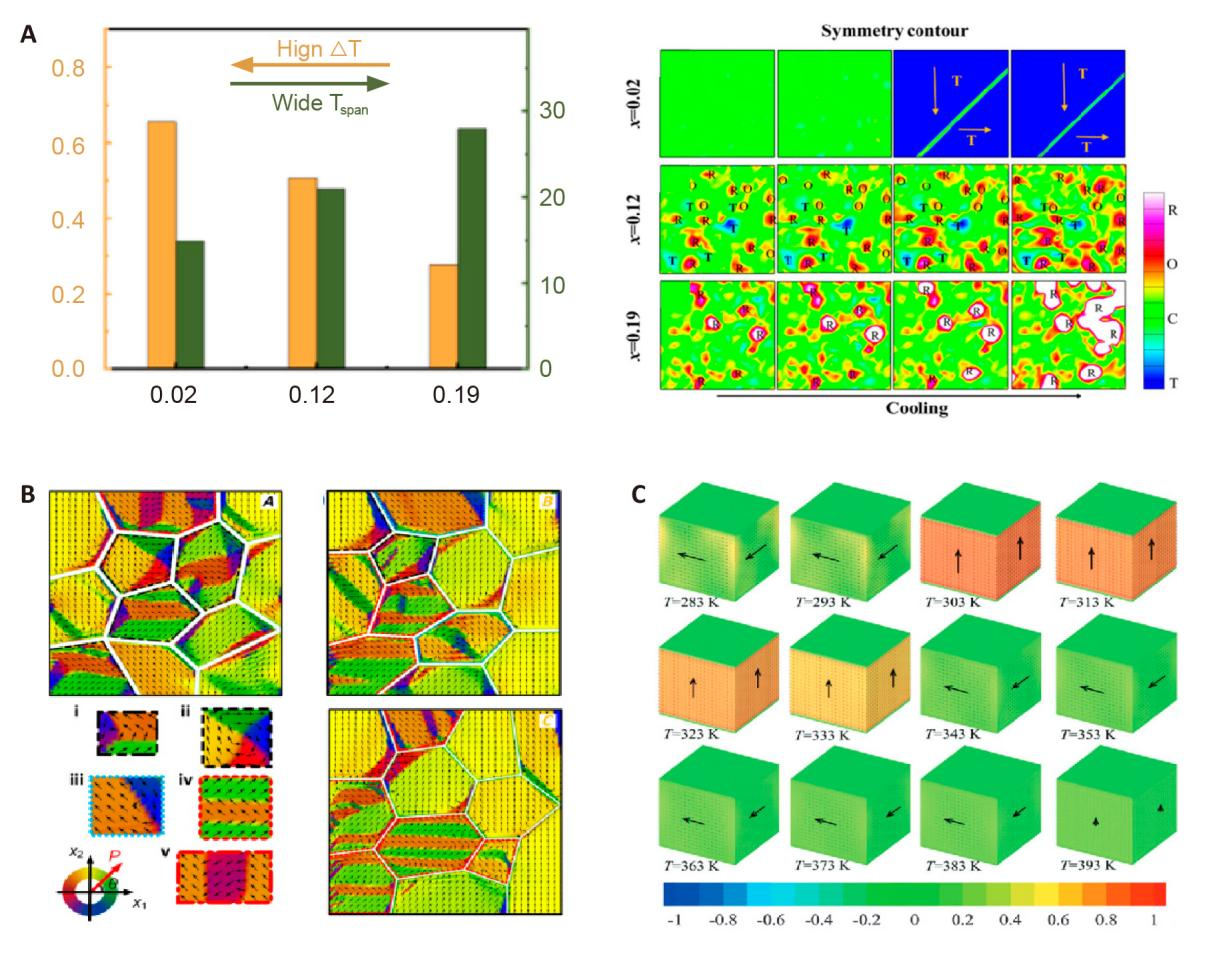
On the other hand, lead-free systems, such as the material BaTiO3 (BTO), which exhibits the best performance, can also be improved through element doping. Wang et al.[19] reported the induction of new ferroelectric material states in the (Ba1-yCay) (Ti1-xSnx) O3 system, including the triple point and the triple relaxor (TR) state at the intersection of the TR region (Figure 2A). They demonstrated that it can lead to significant dielectric response and enhanced electrocaloric performance over a wide temperature range. The TR composition BC0.22 TS0.12 exhibited a relatively high peak (ΔT=0.5K, Tspan=21K) over a broad temperature range. Microstructural features and results from phase-field simulations suggest that the excellent performance arises from the unique microstructure mixing polar nanoregions with tetragonal, orthorhombic, and rhombohedral phases over a wide temperature range. This study provides new insights and strategies for understanding and designing advanced ferroelectric materials with high performance and thermal stability.

 

 

Figure 2. Phase-field simulation of ECEs during ferroelectric phase transition. A: Comparison of the adiabatic temperature change ΔT and temperature stability Tspan for BC0.22TSx materials and microstructural evolution of trirelaxor systems upon cooling the BC0.22TSx system denoted by a symmetry contour, reproduced from Ref.[19] with permission from ACS publications; B: Domain structures and ECEs of PbTiO3 (PTO) polycrystalline ferroelectrics with different grain sizes, reproduced from Ref.[20] with permission from Purpose-Led Publishing; C: The domain structures of the BTO nanoparticles, reproduced from Ref.[21] with permission from Royal Society of Chemistry.

 

The factors mentioned above that influence the ferroelectric-to-paraelectric phase transition are all internal to the material. However, external stimuli also impact the ferroelectric-to-paraelectric phase transition, primarily by affecting the magnitude of polarization along the electric field direction and the polarization variation with temperature, thereby delaying or promoting the occurrence of the phase transition. This, in turn, affects ferroelectric properties such as the magnitude and temperature range of the ECE. Due to limitations in experimental methods and conditions for applying stress/strain to ferroelectric materials, researchers have undertaken a series of theoretical studies. Hou et al.[20] investigated the effect of grain size of polycrystalline ferroelectric materials on their electrocooling effect using a phase-field model based on the temporal Ginzburg-Landau equation (Figure 2B), and found that an increase in grain size can significantly increase the value of adiabatic temperature change of the material and lead to the maximum temperature change occurring at higher temperatures, a finding that provides a new perspective for the optimization of solid-state refrigeration device performance.

 

Based on thermodynamic analysis and phase-field simulations of tetragonal-phase BTO nanoparticles, Wu et al. proposed the innovative concepts of pressure-induced pseudo-first-order phase transition[22] and electric field-induced pseudo-fine phase transition (EFIPPT)[21]. Both types of pseudo-fine phase transitions are caused by domain transformations below the Tc. The maximum adiabatic temperature change and its corresponding temperature vary with the magnitude of the applied pressure stress and external electric field. Domain transformations lead to enhancement or reduction of polarization along the electric field direction, resulting in the simultaneous presence of positive and negative electrode effects in the same material. In Zhang’s study, both electric field and pressure were applied in the x3 direction. Additionally, as shown in Figure 2C, under certain pressure stress and electric field conditions, the abc phase appears in BTO particles, and the transition between the abc phase and the c phase is defined as EFIPPT.

 

3.2 Electric-field-induced Phase Transition

The ferroelectric-to-antiferroelectric phase transition is a phenomenon of significant importance in the fields of materials science and electronics. It involves changes in the internal electronic structure and lattice arrangement of materials, thereby affecting their electromagnetic properties. This phase transition process is not only crucial for understanding the fundamental physical properties of materials but also demonstrates tremendous potential and value in practical applications. Of particular interest is the negative ECE, where the material’s temperature decreases upon the application of an external electric field and increases upon its removal. As depicted in Figure 3A, in perovskite antiferroelectric materials, the positive and negative charge centers do not coincide, forming adjacent antiparallel dipoles. Such an ordered structure results in low structural entropy in the material. When an external electric field is applied, polarization opposite to the field direction undergoes reversal, leading to an increase in the component of polarization entropy perpendicular to the electric field direction, while the component along the electric field direction remains almost unchanged. Consequently, the material’s polarization entropy increases, causing a decrease in temperature under adiabatic conditions, resulting in the negative ECE. Experimentally, negative electrocaloric temperature changes of up to 10K have been measured through compositional tuning, attracting widespread attention. Phase-field simulations can provide a mesoscopic-level understanding of the ferroelectric-to-antiferroelectric phase transition mechanism and offer theoretical guidance for the design of high-performance negative electrocaloric materials through parameter optimization.

 

Figure 3. Phase-field Simulation of ferroelctric-to-antiferroelctric phase transition. A: The schematic of the ABO3 perovskite lattice with antiparallel polarization; B: PZO-based λ-g phase diagram, reproduced from Ref.[4] with permission from ACS publications; C: AFE domain switching versus external electric field along [110] direction. With the increase of the applied field, the polarization starts switching at the antiferroelectric domain boundaries, reproduced from Ref.[26] with permission from IOP Publishing.

 

The phenomenological model of antiferroelectric materials was initially proposed by Kittel, utilizing a model composed of adjacent alternating antiparallel dipoles to describe antiferroelectricity. In recent years, various high-resolution electron microscopes, such as high-angle annular dark-field scanning transmission electron microscopy, have been increasingly used to characterize the microstructure of antiferroelectric materials. A growing body of research indicates that the polarization structure of PbZrO3 (PZO) is very close to the phenomenological model of sublattice antiparallel dipoles induced by next-nearest-neighbor interactions. Xue et al.[23] proposed a three-dimensional phenomenological model based on the Ginzburg-Landau-Devonshire theory to describe the ferroelectric-to-antiferroelectric phase transition in the Sm-doped BiFeO3 system. This model can intricately describe the phase transition induced by temperature, pressure, and composition variations and construct corresponding temperature-composition and temperature-pressure phase diagrams. Geng et al.[24] conducted phase-field simulations to study the field-induced antiferroelectric-to-ferroelectric phase transition phenomenon in nonlinear dielectric composite materials, along with the associated nonlinear dielectric behavior. The simulations revealed the microscopic nucleation and growth mechanisms during the phase transition process. The study suggests that the macroscopic properties of composite materials are highly sensitive to the orientation of antiferroelectric filler particles, making filler morphology an effective control variable in the design of nonlinear dielectric composite materials.

 

Liu et al.[25] corrected the ferroelectric phase-field model by introducing a high-order gradient energy term and coupling the tilt and twist angles of the oxygen octahedra with the gradient energy coefficient, thereby achieving better agreement between the phase-field model and experimental results. Xu et al.[4] further investigated the influence of the high-order gradient energy coefficient g and the first-order gradient energy coefficient λ in the modified antiferroelectric phase-field model on the antiferroelectric phase and plotted the λ-g phase diagram (Figure 3B). The study revealed that the stability of antiferroelectric domains is positively correlated with the gradient energy coefficient g, while an increase in λ makes the antiferroelectric phase more stable. When the ratio of λ to g exceeds a critical value, the isotropy of antiferroelectric domain structures is disrupted, leading to the formation of vortex structures. Zhu et al.[26] simulated the polarization reversal behavior of antiferroelectric domain structures under an external electric field. Under the influence of the external electric field, ferroelectric domains tend to nucleate at the boundaries of antiferroelectric domains, and samples with initially larger antiferroelectric domain sizes exhibit higher coercive fields, a result confirmed by hysteresis loops.

 

4 DOMAIN SWITCHING

Domain switching is another very important topic in the field of ferroelectrics. Although domain switching occurs during phase transitions, in this chapter, we focus on the dynamic processes of ferroelectric domain switching behavior. These include phenomena such as the hysteresis of ferroelectric polarization under electric field reversal[27,28], the nucleation process of ferroelectric domain switching[29], the mechanisms of domain switching[30-32], various factors affecting domain switching, and the behavioral differences of domain switching in different types of ferroelectric materials. Here, we briefly discuss two aspects.

 

4.1 Electric Field Induced Domain Switching

The most prominent characteristic of ferroelectric materials is the hysteresis loop, which manifests as nonlinear increases in polarization with increasing electric field until saturation is reached, after which it exhibits a linear relationship with the electric field. Upon gradual removal of the electric field, residual polarization persists until a certain electric field is applied in the opposite direction, initiating polarization reversal. Currently, the explanation for this hysteresis phenomenon is attributed to the lag in the switching of domains within the ferroelectric material under an applied electric field. Conventional experiments can only measure the hysteresis loop of ferroelectric materials, making it difficult to effectively observe the dynamic changes of domains at the mesoscopic scale, and controlling factors that can affect the shape of the hysteresis loop is also challenging. On the other hand, the emergence and development of piezoelectric force microscopy (PFM) technology, along with advancements in thin film technology, have made it possible to study localized domain switching on high-quality thin films. However, the electric field distribution applied by PFM probes is highly concentrated and non-uniform, often involving complex electrochemical-mechanical interactions, which significantly differ from macroscopic domain switching behavior. Phase-field simulations can conveniently simulate macroscopic hysteresis phenomena and localized domain switching behavior by setting different mechanical and electrical boundary conditions and applying various types of external electric fields, thereby obtaining corresponding spatial distributions of polarization and strain.

 

Phase-field simulations for the study of domain switching behavior in ferroelectrics began with investigations on bulk single crystals in two dimensions. Wang et al.[27] successfully obtained macroscopic P-E hysteresis loops through phase-field simulations of the polarization evolution process under an electric field for tetragonal phase PTO. Their further work[33] predicted that under appropriate equi-biaxial strain, tensile and compressive strains could respectively expand or contract the P-E loop. Soh et al.[34] discovered that under sufficiently large uniaxial compressive strains, a single P-E loop might transition to a double P-E loop resembling antiferroelectric behavior, attributing it to the 180° switching being divided into two 90° switching. The aforementioned phase-field simulations were all based on tetragonal phase PTO, which has only four variants in two dimensions.

 

With the advancement of computer technology, phase-field simulations can now be conducted on larger scales, allowing for the study of various factors affecting the hysteresis loop. Firstly, the influence of mixed phases on the hysteresis loop is examined. Three-dimensional phase-field models were constructed by Choudhury et al.[35] to investigate the domain switching behavior of PZT near morphotropic phase boundaries. They found that the coexistence of multiple phases (tetragonal, rhombohedral, monoclinic) leads to more complex domain configurations and narrows the P-E loop. Such conclusions are further demonstrated in phase-field simulations of relaxor ferroelectrics. In relaxor ferroelectrics, the dominance of short-range interactions due to chemical anisotropy replaces long-range ferroelectric ordering, resulting in the formation of polar nanoregions instead of large domains. Consequently, the hysteresis phenomenon in relaxor ferroelectrics is significantly weakened, leading to exceptionally high piezoelectric performance. A phase-field model incorporating the random field theory was proposed by Wang et al.[36] to simulate the domain switching behavior of relaxor ferroelectrics. In this model, the weakening of the hysteresis loop in relaxor ferroelectrics is associated with the reduction in domain size induced by the introduction of random fields. Another phase-field model was proposed by Pan et al.[37] to elucidate the weakening of hysteresis in the super-paraelectric relaxor ferroelectric Sm-BFBT. By introducing two sets of potential functions in the model to describe Sm-BFO and Sm-BTO phases separately, with the ferroelectric phase Sm-BFO being treated as spherical, they obtained results consistent with experiments. They revealed that under super-paraelectric states, nanodomains further shrink and the coupling between domains weakens, leading to a decrease in energy barriers and achieving highly dynamic polarization reversal, which is crucial for achieving small hysteresis behavior. Additionally, phase-field simulations also incorporate structural defects (such as dislocations) and study their influence on ferroelectric domain reversal, providing a mesoscopic understanding of the pinning effect of dislocations during domain switching and their impact on the shape of the P-E loop[38-40].

 

The discussions above have assumed single-crystal ferroelectric materials. However, the polycrystalline structure of ferroelectric ceramics and their domain structures also affect the hysteresis loop, especially when grain sizes are reduced to the nanoscale[41]. Choudhury et al.[42] initially proposed a phase-field model for ferroelectric polycrystals. Their further work demonstrated that phase-field simulations reveal the effects of grain orientation, grain boundaries, and grain size on ferroelectric domain switching and stress distribution. Specifically, grain orientation and grain boundaries play crucial roles in domain nucleation and stress concentration, while a reduction in grain size lowers the transformation temperature, affecting polarization and domain structure[43]. Subsequently, similar ferroelectric polycrystal models have been applied to study the effects of grain orientation[44], grain boundary semiconductivity, and grain boundary width[45] on domain switching behavior. Generally, as grain size decreases and differences in grain orientation increase, the P-E loop contracts. Additionally, increased grain boundary conductivity leads to significant tilting and shrinkage of the P-E loop. Su et al.[41,46,47] further systematically investigated this topic, with grain sizes in their model reduced to as small as 10 nm, and cyclic electric field frequencies reaching up to 2,500Hz. They found that the closure of flux-closed domains due to strong depolarization fields results in the tilting and disappearance of the P-E loop when grains are refined to the nanoscale. Vidyasagar and colleagues[48] effectively predicted the homogenized response of polycrystalline ferroelectric materials like barium titanate and lead zirconate titanate under electric fields using an improved spectral phase-field method. This approach addressed the challenges faced by traditional methods in handling periodic microstructures, studying the impact of microstructure on the electro-mechanical coupling response of materials. They also reduced the instability in spectral techniques through finite difference corrections. Indergand et al.[49] proposed a polycrystalline phase-field model for ferroelectric ceramics that considers temperature effects. Their simulations revealed the impact of temperature on the polarization reversal dynamics of ferroelectric materials, predicting trends in spontaneous polarization, coercive field, and piezoelectric properties with temperature changes, which aligned with experimental data. Sugathan et al.[50] developed a computational method combining phase-field modeling and genetic algorithms to simulate the ferroelectric switching behavior of polycrystalline hafnium zirconium oxide (HZO) thin films. Their study optimized effective Landau coefficients describing the free energy of HZO, validating the model’s accuracy through simulations of the P-E loops of HZO films with different ferroelectric phase fractions. The simulation results also provided fundamental insights into enhancing the ferroelectric performance of HZO films by controlling grain morphology and crystal orientation. Schultheiß and colleagues[51] conducted an in-depth study of domain structure evolution and its correlation with material properties in ferroelectric materials through phase-field simulations. They revealed the influence of factors such as grain size, crystal orientation, and porosity on domain wall dynamics.

 

In addition to using global electric fields to induce domain switching in ferroelectric materials experimentally, localized electric fields applied by scanning probes in PFM are also employed. Many researchers have introduced the tip-induced electric field from PFM probes into phase-field models and studied its effects. In phase-field models considering the bias voltage applied by PFM tips, its spatial distribution is approximated using a Lorentz-like function to represent the surface electrostatic potential distribution φ generated by a point charge at a distance away from the surface of the film.

 

 

In the equation (8), (x1, x2) represents the coordinate system on the surface, denotes the position of the tip, i.e., the position where the potential is at its peak value Φ0, and γ is the distance from the tip where the peak potential decreases to half. By incorporating this potential distribution into the electrical boundary conditions on the upper surface, one can simulate the electric field induced by PFM as well as the corresponding local domain switching behavior. Although some studies have constructed analytical or semi-analytical models for the switching induced by PFM probes[32], phase-field models offer a more convenient way to reveal the temporal evolution of domain switching, estimate changes in energy density and field distribution during the switching process, thus providing possibilities for a more comprehensive understanding of the nanoscale dynamics of local domain switching[52]. Phase-field simulations have been used to investigate various aspects of local domain switching induced by PFM probes, including the critical bias voltage for nucleation[29,53-56], domain wall mobility[57,58], as well as the mechanisms behind mesoscopic-scale local domain switching[30-32], the existence of ferroelectric/ferroelastic domain walls in the initial state[30,31,53,58], and the impacts of misfit dislocations and grain boundaries on local domain switching[59].

 

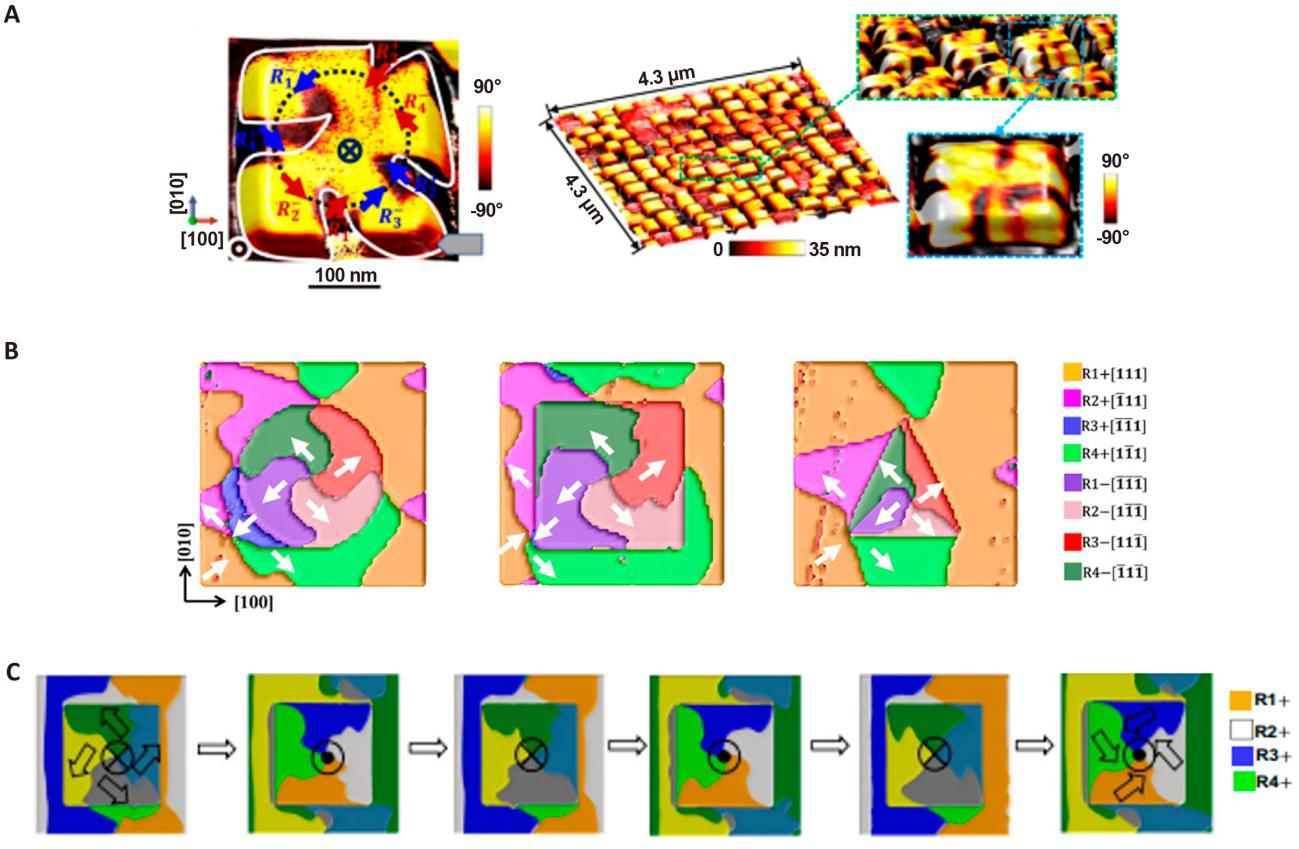
Figure 4. Phase-field simulation of domain switching in BFO and corresponding experiment results. A: A large-scale BiFeO3 nanocrystal array with the magnified OOP domain patterns and the construction of OOP and IP polarization projection for a BiFeO3 nanocrystal by PFM measurement, reproduced from Ref.[60] with permission from Springer Nature; B: Phase-field simulation of the polarization vector map induced by different shape of surface charge on BFO thin film, reproduced from Ref.[61] with permission from IOP Publishing; C: Reversible vortex chirality evolution under the surface charge stimuli, reproduced from Ref.[62] with permission from Springer Nature.

 

In addition to directly controlling domain switching behavior in ferroelectric domains using PFM probes with applied electric fields, surface charges on ferroelectric materials also significantly influence domain switching behavior. Wang et al.[60] discovered polar Solomon rings in ferroelectric nanocrystals through experimental observation and phase-field simulation, and demonstrated their reversible topological phase transitions under electric-field modulation as well as their unique properties in terahertz-wave absorption (Figure 4A). Ma et al.[63] investigated the control of the conductivity of center-type tetra-domain structures in self-assembled BFO nanoislands via electric fields. These self-assembled nanoislands can achieve reversible switching of center-type tetra-domain structures under the action of an electric field, thereby altering the conductivity of domain walls. This discovery provides a new pathway for realizing low-energy, non-volatile ferroelectric memory devices. The effect of surface charge shape on the structure and domain percentage of ferroelectric vortex domains in BiFeO3 thin films is revealed by Liu et al.[61] using phase-field simulation, providing an in-depth theoretical basis for domain manipulation in ferroelectric materials (Figure 4B). Chen et al.[64] reported robust polarization switching in self-assembled BFO nanoislands. These nanoislands possess center-type tetra-domain structures, where each quarter region can independently undergo polarization switching, exhibiting excellent retention properties. This offers potential storage units for high-density ferroelectric random-access memory applications. Liu et al.[62] also investigated the influence of surface charges on the ferroelectric vortex structure in BFO thin films through phase-field simulations. The study revealed that the distribution shape of surface charges significantly affects the proportion of four-quadrant topological domains (4R domains) within the vortex (Figure 4C). This suggests that by changing the shape of surface charges, the structure and proportion of vortex domains can be manipulated, providing possibilities for applications such as high-density information storage. Researchers also studied the manipulation of vortex chirality in ferroelectric thin films through phase-field simulations. The study demonstrated that by applying local surface charges or electric fields, the chirality and polarity of vortices can be controlled. This control is achieved by changing the initial arrangement of dipole pairs and the direction of the external electric field, with the vortex chirality remaining stable even after the removal of the external electric field. These findings are of great significance for the development of novel memory devices and understanding the fundamental physical properties of ferroelectric materials. By precisely controlling domain switching behavior, as well as the morphology and chirality of domain walls, new avenues can be opened for future nanoelectronics and information storage technologies.

 

4.2 Mechanically Induced Domain Switching

Stress, as another typical external stimulus, can induce phase transition behavior in various materials[65-67]. Inducing domain switching in ferroelectric domains can also be achieved by applying a force field (stress or strain) to the ferroelectric material. The most common method involves growing ferroelectric thin films epitaxially on substrates, utilizing the mismatch strain between the substrate and the film to induce domain switching. Choudhury et al.[28] first utilized phase-field simulations to study the effects of mismatch strain on the domain switching behavior of (001) BTO thin films. Their work explained the non-monotonic dependence of domain switching on the misfit strain, which arises from the complex domain structure in the mixed-phase regions. Recently, Zhang et al.[68] conducted more systematic phase-field simulations, providing a detailed analysis of the ferroelectric domain switching behavior in BTO thin films and the dependence on mismatch strain, film thickness, and field frequency, comparing their results with corresponding experimental findings.

 

Another method of inducing domain switching in ferroelectric domains using a force field is by utilizing atomic force microscopy (AFM) to locally switch ferroelectric polarization in specific regions. Besides the piezoelectric effect, this method also involves another electromechanical interaction known as flexoelectric effect. The flexoelectric effect arises from polarization changes due to strain gradients, which, while negligible at the macroscopic scale, play an increasingly important role at the micro and nanoscale[69]. Lu et al.’s research[70] discovered that mechanical force applied by an AFM tip can switch ferroelectric polarization in ultra-thin ferroelectric materials, attributing this phenomenon to the flexoelectric effect. This finding sparked interest in mechanically induced polarization switching at the nanoscale. However, due to the complex interactions[71] between the AFM probe and the ferroelectric film surface, involving various ion and electrochemical processes[72], it is necessary to decouple multiple physical and chemical actions using phase-field simulations to elucidate the mechanism of mechanical switching. The contribution of flexoelectricity can be incorporated into the total free energy as a Lifshitz term, thereby considering both the intrinsic strain induced by polarization gradients and the polarization dynamics induced by strain gradients, also known as the flexoelectric field. The mechanical force exerted by the AFM probe on the film surface is assumed to follow Hertzian contact mechanics with a spherical indenter, leading to a surface stress distribution σ33(r), which can be expressed as:

 

 

Where a represents the radius of the contact area, which can be calculated using the applied mechanical force p and the tip radius r. Incorporating this formula into the mechanical boundary conditions on the surface of the film, which are used to solve the elastic equilibrium equations, allows for simulating the influence of an AFM probe on the domain switching behavior of ferroelectric films.

 

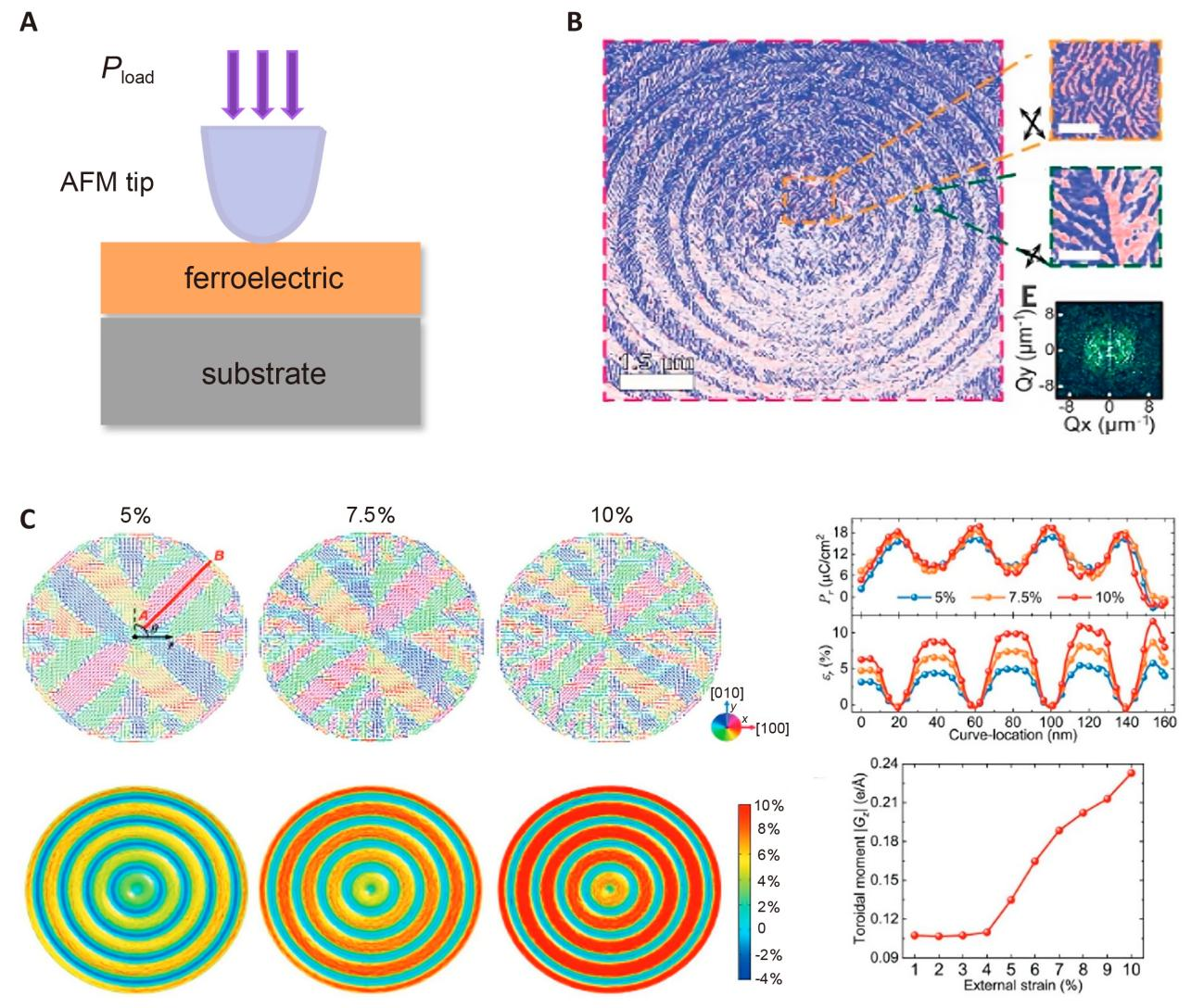
Gu et al.[73] introduced the flexoelectric field into a ferroelectric phase-field model, demonstrating its significant role in the mechanical switching process of ferroelectric films. Simulation results showed that the flexoelectric field beneath an AFM tip could reach 107V/m, sufficient to induce ferroelectric domain switching. Researchers also compared the roles of the piezoelectric effect and the flexoelectric effect in polarization reversal. By toggling the flexoelectric effect on and off, they identified the flexoelectric field as the primary factor driving polarization reversal. Chen et al.[74] combined surface effects with the flexoelectric effect in phase-field simulations and found that when surface screening fell below a critical value, local domain switching transitioned to propagating domain switching. This transition was accompanied by a “ripple effect” in domain switching, forming concentric ring domain patterns under local excitation. Such domain patterns underwent further investigation. Guo et al.[75] discovered periodic ring-shaped “target-like” wrinkling patterns in flexible ferroelectric polymer polyvinylidene fluoride-trifluoroethylene (P(VDF-TrFE)), and using in-plane piezoresponse force microscopy (IP-PFM), they measured a distinct ring-shaped topological texture (Figure 5B). The distribution of ring domains was induced by the “target-like” wrinkling morphology under external tensile strain, characterized by periodic alternating tensile and compressive strains. Based on these calculations, the polar ring moment Gz was significantly greater than Gx and Gy, indicating the existence of in-plane ring order. Guo et al.[76] further employed phase-field simulation methods to delve into the evolution of strain-induced circulating polarization structures in P(VDF-TrFE) thin films featuring concentric ring wrinkle patterns. The study revealed the morphological and thickness dependence of these circulating polarization topological structures in wrinkled P(VDF-TrFE) films under different thicknesses and morphologies. As depicted in Figure 5C, through phase-field simulations, the authors also investigated the opposite alignment of ferroelectric polarization directions at the top and bottom surfaces of the films due to periodic variations in the strain field, providing the possibility of utilizing this unique polarization arrangement for data storage purposes.

 

Figure 5. Phase-field simulation of mechanically induced domain switching. A: Schematic of mechanical switching by an AFM tip; B: IP-PFM phase image showing hierarchical structures of the toroidal pattern reproduced from Ref.[75] with permission from AAAS; C: Polarization and strain distribution of wrinkled P(VDF-TrFE) films at various tensile strains, reproduced from Ref.[76] with permission from Wiley-VCH Verlag.

 

5 CONCLUSION AND OUTLOOK

In this paper, we delve into the important role of phase-field simulations in the study of ferroelectric phase transitions and domain flips. Through the phase-field approach, we are able to simulate and predict the spatiotemporal evolution of the microstructure of ferroelectric materials as well as the response to external fields, thus shedding light on the diverse domain structures and phase transition processes in ferroelectric materials. The article begins with an overview of the fundamental framework of the phase-field model and a comprehensive review of the various phase transitions in ferroelectric materials, including the ferroelectric-cis and antiferroelectric-ferroelectric transitions. In addition, the paper summarizes the research results of ferroelectric domain switching induced by various experimental stimuli (e.g., electric and force fields).

 

Looking ahead, the application of phase field simulation methods in the field of ferroelectric materials research is promising. With the increasing computational power and further development of simulation techniques, we are expected to understand the complexity of ferroelectric materials at a higher level. Future research can focus on the following directions: first, to improve the accuracy and computational efficiency of phase-field models to better simulate the complex phenomena in real materials; second, to explore new experimental techniques combined with phase-field simulations to validate and optimize the simulation results; and third, to use phase-field simulations to guide the design and synthesis of new materials, especially in the fields of high-performance memory devices, sensors, and actuators.

 

In addition, with the deeper understanding of the domain structure and phase transition mechanism of ferroelectric materials, we can expect breakthroughs in nanoelectronics and information storage technologies. By precisely controlling the domain switching behavior as well as the morphology and chirality of domain walls, new paths will be opened for future nanoelectronics and information storage technologies. In conclusion, phase-field simulations will continue to serve as an important tool for understanding the fundamental physical properties of ferroelectric materials and for advancing the development of related application technologies.

 

Acknowledgments

This work was supported financially by the National Natural Science Foundation of China (Grant No.52372100) and the National Key Research and Development Program of China (Grant No.2019YFA0307900).

 

Conflicts of Interest

All authors declared that there are no conflicts of interest.

 

Author Contribution

Huang H and Tang S both conceived, designed the manuscript and drafted, revised the manuscript.

 

Abbreviation List

AFM, Atomic force microscopy

TC, Curie temperature

EFIPPT, Electric field-induced pseudo-fine phase transition

ECE, Electrocaloric effect

HZO, Hafnium zirconium oxide

IP, In-plane

PFM, Piezoelectric force microscopy

P-E, Polarization-electric field

P(VDF-TrFE), Polyvinylidene fluoride-trifluoroethylene

RT, Room temperature

TR, Triple relaxor

 

References

[1] Scott JF, Paz De Araujo CA. Ferroelectric Memories. Science, 1989; 246: 1400-1405.[DOI]

[2] Hamlehdar M, Kasaeian A, Safaei MR. Energy harvesting from fluid flow using piezoelectrics: A critical review. Renew Energ, 2019; 143: 1826-1838.[DOI]

[3] Sun X, Huang H, Wang J et al. Strain-induced broadening temperature range of electrocaloric effects in ferroelectric superlattices. J Alloy Compd, 2019; 777: 821-827.[DOI]

[4] Xu K, Shi X, Dong S et al. Antiferroelectric Phase Diagram Enhancing Energy-Storage Performance by Phase-Field Simulations. Acs Appl Mater Inter, 2022; 14: 25770-25780.[DOI]

[5] Liang D, Chen LQ, Huang H. A simple displacement perturbation method for phase-field modeling of ferroelectric thin film. Acta Mater, 2024; 276: 120104.[DOI]

[6] Guo C, Huang H. Design of super-elastic freestanding ferroelectric thin films guided by phase-field simulations. Microstructures 2022; 2: 2022021.[DOI]

[7] Li YL, Hu SY, Liu ZK et al. Effect of substrate constraint on the stability and evolution of ferroelectric domain structures in thin films. Acta Mater, 2002; 50: 395411.[DOI]

[8] Schrade D, Mueller R, Xu BX et al. Domain evolution in ferroelectric materials: A continuum phase field model and finite element implementation. Comput Method Appl M, 2007; 196: 4365-4374.[DOI]

[9] Krauß M, Münch I. A selective enhanced FE-method for phase field modeling of ferroelectric materials. Comput Mech, 2016; 57: 105-122.[DOI]

[10] Zhang W, Bhattacharya K. A computational model of ferroelectric domains. Part I: model formulation and domain switching. Acta Mater, 2005; 53: 185-198.[DOI]

[11] Qiu JH, Ding JN, Yuan NY et al. Composition and misfit strain dependence of electrocaloric effect of Pb1-xSrxTiO3 thin films. Chinese Phys B, 2013; 22: 017701.[DOI]

[12] Mischenko AS, Zhang Q, Scott JF et al. Giant Electrocaloric Effect in Thin-Film PbZr0.95Ti0.05O3. Science, 2006; 311: 1270-1271.[DOI]

[13] Karthik J, Martin LW. Effect of domain walls on the electrocaloric properties of Pb(Zr1-x,Tix)O3 thin films. Appl Phys Lett, 2011; 99: 032904.[DOI]

[14] Qiu JH, Jiang Q. Effect of electric field on electrocaloric effect in Pb(Zr1-xTix)O3 solid solution. Phys Lett A, 2008; 372: 7191-7195.[DOI]

[15] Bai G, Qin X, Xie Q et al. Electric-field-induced phase transition and electrocaloric effect in PZT near morphotropic phase boundary. Physica B, 2019; 560: 208-214.[DOI]

[16] Li B, Wang JB, Zhong XL et al. Room temperature electrocaloric effect on PbZr0.8Ti0.2O3 thin film. J Appl Phys, 2010; 107: 014109.[DOI]

[17] Qiu JH, Jiang Q. Misfit strain dependence of electrocaloric effect in epitaxial Pb(Zr1-xTix)O3 thin films. J Appl Phys, 2008; 103: 084105.[DOI]

[18] Wang F, Li B, Ou Y et al. Multicaloric effects in PbZr0.2Ti0.8O3 thin films with 90° domain structure. EPL, 2017; 118: 17005.[DOI]

[19] Wang Y, Wang D, Xu J et al. Trirelaxor Ferroelectric Material with Giant Dielectric Permittivity over a Wide Temperature Range. Acs Appl Mater Inter, 2021; 13: 33272-33281.[DOI]

[20] Hou X, Li X, Zhang J et al. Effect of Grain Size on the Electrocaloric Properties of Polycrystalline Ferroelectrics. Phys Rev Appl, 2021; 15: 054019.[DOI]

[21] Wu HH, Zhu J, Zhang TY. Double hysteresis loops and large negative and positive electrocaloric effects in tetragonal ferroelectrics. Phys Chem Chem Phys, 2015; 17: 23897-23908.[DOI]

[22] Wu HH, Zhu J, Zhang TY. Pseudo-first-order phase transition for ultrahigh positive/negative electrocaloric effects in perovskite ferroelectrics. Nano Energy, 2015; 16: 419-427.[DOI]

[23] Xue F, Liang L, Gu Y et al. Composition- and pressure-induced ferroelectric to antiferroelectric phase transitions in Sm-doped BiFeO3 system. Appl Phys Lett, 2015; 106: 012903.[DOI]

[24] Geng LD, Jin YM, Tan DQ et al. Computational study of nonlinear dielectric composites with field-induced antiferroelectric-ferroelectric phase transition. J Appl Phys, 2018; 124: 164109.[DOI]

[25] Liu Z, Xu BX. Insight into perovskite antiferroelectric phases: Landau theory and phase field study. Scripta Mater, 2020; 186: 136-141.[DOI]

[26] Zhu J, Liu Z, Zhong B et al. Domain size and charge defects affecting the polarization switching of antiferroelectric domains. Chinese Phys B, 2023; 32: 047701.[DOI]

[27] Wang J, Shi SQ, Chen LQ et al. Phase-field simulations of ferroelectric/ferroelastic polarization switching. Acta Mater, 2004; 52: 749-764.[DOI]

[28] Choudhury S, Li YL, Chen LQ et al. Strain effect on coercive field of epitaxial barium titanate thin films. Appl Phys Lett, 2008; 92: 142907.[DOI]

[29] Choudhury S, Zhang JX, Li YL et al. Effect of ferroelastic twin walls on local polarization switching: Phase-field modeling. Appl Phys Lett, 2008; 93: 162901.[DOI]

[30] Hong Z, Britson J, Hu JM et al. Local 90° switching in Pb(Zr0.2Ti0.8)O3 thin film: Phase-field modeling. Acta Mater, 2014; 73: 75-82.[DOI]

[31] Britson J, Gao P, Pan X et al. Phase field simulation of charged interface formation during ferroelectric switching. Acta Mater, 2016; 112: 285-294.[DOI]

[32] Morozovska AN, Eliseev EA, Li Y et al. Thermodynamics of nanodomain formation and breakdown in scanning probe microscopy: Landau-Ginzburg-Devonshire approach. Phys Rev B, 2009; 80: 214110.[DOI]

[33] Wang J, Li Y, Chen L et al. The effect of mechanical strains on the ferroelectric and dielectric properties of a model single crystal - Phase field simulation. Acta Mater, 2005; 53: 2495-2507.[DOI]

[34] Soh AK, Song YC, Ni Y. Phase Field Simulations of Hysteresis and Butterfly Loops in Ferroelectrics Subjected to Electro‐Mechanical Coupled Loading. J Am Ceram Soc, 2006; 89: 652-661.[DOI]

[35] Choudhury S, Chen LQ, Li YL. Correlation between number of ferroelectric variants and coercive field of lead ziconate titanate single crystals. Appl Phys Lett, 2007; 91: 032902.[DOI]

[36] Wang S, Yi M, Xu BX. A phase-field model of relaxor ferroelectrics based on random field theory. Int J Solids Struct, 2016; 83: 142–153.[DOI]

[37] Pan H, Lan S, Xu S et al. Ultrahigh energy storage in superparaelectric relaxor ferroelectrics. Science, 2021; 374: 100-104.[DOI]

[38] Wu HH, Wang J, Cao SG et al. Micro-/macro-responses of a ferroelectric single crystal with domain pinning and depinning by dislocations. J Appl Phys, 2013; 114: 164108.[DOI]

[39] Li YL, Hu SY, Choudhury S et al. Influence of interfacial dislocations on hysteresis loops of ferroelectric films. J Appl Phys, 2008; 104: 104110.[DOI]

[40] Wu HH, Wang J, Cao SG et al. Effect of dislocation walls on the polarization switching of a ferroelectric single crystal. Appl Phys Lett, 2013; 102: 232904.[DOI]

[41] Su Y, Kang H, Wang Y et al. Intrinsic versus extrinsic effects of the grain boundary on the properties of ferroelectric nanoceramics. Phys Rev B, 2017; 95: 054121.[DOI]

[42] Choudhury S, Li Y, Krilliii C et al. Phase-field simulation of polarization switching and domain evolution in ferroelectric polycrystals. Acta Mater, 2005; 53: 5313-5321.[DOI]

[43] Choudhury S, Li YL, Krill Iii C et al. Effect of grain orientation and grain size on ferroelectric domain switching and evolution: Phase field simulations. Acta Mater, 2007; 55: 1415-1426.[DOI]

[44] Wang J, Shu W, Shimada T et al. Role of grain orientation distribution in the ferroelectric and ferroelastic domain switching of ferroelectric polycrystals. Acta Mater, 2013; 61: 6037-6049.[DOI]

[45] Shu W, Wang J, Zhang TY. Effect of grain boundary on the electromechanical response of ferroelectric polycrystals. J Appl Phys, 2012; 112: 064108.[DOI]

[46] Su Y, Liu N, Weng GJ. A phase field study of frequency dependence and grain-size effects in nanocrystalline ferroelectric polycrystals. Acta Mater, 2015; 87: 293-308.[DOI]

[47] Liu N, Su Y, Weng GJ. A phase-field study on the hysteresis behaviors and domain patterns of nanocrystalline ferroelectric polycrystals. J Appl Phys, 2013; 113: 204106.[DOI]

[48] Vidyasagar A, Tan WL, Kochmann DM. Predicting the effective response of bulk polycrystalline ferroelectric ceramics via improved spectral phase field methods. J Mech Phys Solids, 2017; 106: 133-151.[DOI]

[49] Indergand R, Vidyasagar A, Nadkarni N et al. A phase-field approach to studying the temperature-dependent ferroelectric response of bulk polycrystalline PZT. J Mech Phys Solids, 2020; 144: 104098.[DOI]

[50] Sugathan S, Thekkepat K, Bandyopadhyay S et al. A phase field model combined with a genetic algorithm for polycrystalline hafnium zirconium oxide ferroelectrics. Nanoscale, 2022; 14: 14997-15009.[DOI]

[51] Schultheiß J, Picht G, Wang J et al. Ferroelectric polycrystals: Structural and microstructural levers for property-engineering via domain-wall dynamics. Prog Mater Sci, 2023; 136: 101101.[DOI]

[52] Kalinin SV, Morozovska AN, Chen LQ et al. Local polarization dynamics in ferroelectric materials. Rep Prog Phys, 2010; 73: 056502.[DOI]

[53] Jesse S, Rodriguez BJ, Choudhury S et al. Direct imaging of the spatial and energy distribution of nucleation centres in ferroelectric materials. Nat Mater, 2008; 7: 209-215.[DOI]

[54] Rodriguez BJ, Choudhury S, Chu YH et al. Unraveling Deterministic Mesoscopic Polarization Switching Mechanisms: Spatially Resolved Studies of a Tilt Grain Boundary in Bismuth Ferrite. Adv Funct Mater, 2009; 19: 2053-2063.[DOI]

[55] Balke N, Choudhury S, Jesse S et al. Deterministic control of ferroelastic switching in multiferroic materials. Nat Nanotechnol, 2009; 4: 868-875.[DOI]

[56] Maksymovych P, Jesse S, Huijben M et al. Intrinsic Nucleation Mechanism and Disorder Effects in Polarization Switching on Ferroelectric Surfaces. Phys Rev Lett, 2009; 102: 017601.[DOI]

[57] Choudhury S, Li Y, Odagawa N et al. The influence of 180° ferroelectric domain wall width on the threshold field for wall motion. J Appl Phys, 2008; 104: 084107.[DOI]

[58] Aravind VR, Morozovska AN, Bhattacharyya S et al. Correlated polarization switching in the proximity of a 180° domain wall. Phys Rev B, 2010; 82: 024111.[DOI]

[59] Gao P, Britson J, Jokisaari JR et al. Atomic-scale mechanisms of ferroelastic domain-wall-mediated ferroelectric switching. Nat Commun, 2013; 4: 2791.[DOI]

[60] Wang J, Liang D, Ma J et al. Polar Solomon rings in ferroelectric nanocrystals. Nat Commu, 2023; 14: 3941.[DOI]

[61] Liu D, Shi X, Wang J et al. Phase-field simulations of surface charge-induced ferroelectric vortex.J Phys D Appl Phys, 2021; 54: 405302.[DOI]

[62] Liu D, Wang J, Jafri HM et al. Phase-field simulations of vortex chirality manipulation in ferroelectric thin films. npj Quantum Mater, 2022; 7: 34.[DOI]

[63] Ma J, Ma J, Zhang Q et al. Controllable conductive readout in self-assembled, topologically confined ferroelectric domain walls. Nat Nanotechnol, 2018; 13: 947-952.[DOI]

[64] Chen M, Ma J, Peng RC et al. Robust polarization switching in self-assembled BiFeO3 nanoislands with quad-domain structures. Acta Mater, 2019; 175: 324-330.[DOI]

[65] Wang JJ, Wu PP, Ma XQ et al. Temperature-pressure phase diagram and ferroelectric properties of BaTiO3 single crystal based on a modified Landau potential. J Appl Phys, 2010; 108: 114105.[DOI]

[66] Ma Z, Liu Z, Lu S et al. Pressure-induced emission of cesium lead halide perovskite nanocrystals. Nat Commun, 2018; 9: 4506.[DOI]

[67] Mazur O, Tozaki K, Yoshimura Y et al. Influence of pressure on the kinetics of ferroelectric phase transition in BaTiO3. Physica A, 2022; 599: 127436.[DOI]

[68] Zhang Q, Xia X, Wang J et al. Effects of epitaxial strain, film thickness and electric-field frequency on the ferroelectric behavior of BaTiO3 nano films. Int J Solids Struct, 2018; 144-145: 32-45.[DOI]

[69] Zubko P, Catalan G, Tagantsev AK. Flexoelectric Effect in Solids. Annu Rev Mater Res, 2013; 43: 387-421.[DOI]

[70] Lu H, Bark CW, Esque De Los Ojos D et al. Mechanical Writing of Ferroelectric Polarization. Science, 2012; 336: 59-61.[DOI]

[71] Vasudevan RK, Balke N, Maksymovych P et al. Ferroelectric or non-ferroelectric: Why so many materials exhibit “ferroelectricity” on the nanoscale. Appl Phys Rev, 2017; 4: 021302.[DOI]

[72] Kalinin SV, Jesse S, Tselev A et al. The Role of Electrochemical Phenomena in Scanning Probe Microscopy of Ferroelectric Thin Films. ACS Nano, 2011; 5: 5683-5691.[DOI]

[73] Gu Y, Hong Z, Britson J et al. Nanoscale mechanical switching of ferroelectric polarization via flexoelectricity. Appl Phys Lett, 2015; 106: 022904.[DOI]

[74] Chen W, Liu J, Ma L et al. Mechanical switching of ferroelectric domains beyond flexoelectricity. J Mech Phys Solids, 2018; 111: 43-66.[DOI]

[75] Guo M, Guo C, Han J et al. Toroidal polar topology in strained ferroelectric polymer. Science, 2021; 371: 1050-1056.[DOI]

[76] Guo C, Dong S, Wang J et al. Strain-Induced Toroidal Polar States in Wrinkled Ferroelectric Polymer by Phase-Field Simulations. Adv Electron Mater, 2023; 9: 2300193.[DOI]

 

Copyright © 2024 The Author(s). This open-access article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, sharing, adaptation, distribution, and reproduction in any medium, provided the original work is properly cited.

 

Brief of Corresponding Author(s)

Houbing Huang He is a Professor of Materials Science and Engineering at Beijing Institute of Technology. He received his Ph.D. degree from the University of Science and Technology Beijing in 2013. His current research interests focus on the phase-field model of multiferroic, ferro/piezo-electric, and ferromagnetic materials. He has published over 200 peer-review papers with H-index of 32, including top journals such as Science, Nature, Nat. Energy, Nat. Mater, Phys. Rev. Lett., Adv. Mater. etc.