Power Control Based on a Proportional-dual Integral Controller for Multi-rotor Wind Power Systems Using Genetic Algorithm

 

Habib Benbouhenni1*

 

1Department of Electrical & Electronics Engineering, Faculty of Engineering and Architecture, Nisantasi University, Istanbul, Turkey

 

*Correspondence to: Habib Benbouhenni, PhD, Professor, Department of Electrical & Electronics Engineering, Faculty of Engineering and Architecture, Nisantasi University, Istanbul, 34481742, Turkey; E-mail: habib.benbouenni@nisantasi.edu.tr

 

DOI: 10.53964/id.2024023

 

Abstract

In this study, the new direct power control (DPC) is proposed based on proportional-dual integral (PDI) controllers to control the doubly-fed induction generator (DFIG) power. The effectiveness of the suggested DPC-PDI strategy is analyzed and compared with traditional DPC techniques in terms of the minimizing steady-state error (SSE), DFIG energy undulations, time response, and total harmonic distortion (THD) of current of the DFIG-based multi-rotor wind turbine (MRWT). Graphical and numerical results show that the DPC-PDI strategy is more robust to parameter variations of the system compared to the conventional DPC. Moreover, the DPC-PDI has low THD compared to the DPC. Also, when the suggested DPC-PDI is used, the SSE and overshoot of the DFIG power is reduced. Detailed simulation results using MATLAB using a 1,500kW DFIG-MRWT are presented, where the THD value was reduced by 13.04%, 5.45%, and 59.25% in the tests compared to the DPC. The DPC-PDI minimized the value of active power ripples by percentages estimated at 83.10%, 87%, and 84.07% in the suggested tests compared to the DPC. Also, the SSE of reactive power was reduced by 70.68%, 84.84%, and 79.85% in the tests compared to the DPC. These percentages indicate the superiority of the DPC-PDI in ameliorating DFIG-MRWT system characteristics compared to the DPC.

 

Keywords: proportional-dual integral (PDI) controllers, doubly-fed induction generator, total harmonic distortion, direct power control, multi-rotor wind turbine system

 

1 INTRODUCTION

Traditionally, many controllers have been proposed as a suitable solution to control the doubly-fed induction generator (DFIG) to obtain electrical energy (EE) from wind energy (WE). These controls vary in principle, robustness, ease of implementation, simplicity, and cost. However, direct power control (DPC) remains one of the most prominent and famous strategies used in the field of renewable powers (RPs) due to the advantages it has[1]. Simplicity, fast dynamic speed, easy to apply, low gain, easy to adjust, and not requiring precise knowledge of the mathematical model (MM) of the system are among the most prominent positives of this strategy[2]. As is known, the DPC relies on the use of both a switching table (ST) and a hysteresis controller (HC) to command power[3]. As is known, the working principle of the DPC strategy is the same as that of the direct torque command (DTC), where the difference between them lies in the controlled amounts. The DPC is based on power estimation, where both current and voltage are measured to first estimate the flux and then estimate the power. In this command, the energy estimate is directly linked to the flux estimate[4]. This strategy does not use inner loops as in field-oriented command (FOC). This strategy was used to command the induction generator in Datta et al.[5], where the MATLAB was used to implement this command. Also, this strategy was applied in order to control the capabilities of the synchronous generator at Alizadeh et al[6]. Using the DPC strategy makes the energy system less complex, with a rapid dynamic response to capacity, which is positive. However, it is noted that there are undulations at the level of torque, power, and currents, and these ripples are larger in the case of a durability test, which makes the power quality decrease, which is negative. Another application of using the DPC strategy was done in the Djazia et al.[7], where this strategy was used to control an active filter. This command was used with phase-locked loop (PLL) to estimate capabilities and increase system stability and robustness. The negative of this strategy is the high ripples in both current and power, which causes many problems in the network, which is undesirable[8]. Also, a significant increase in the total harmonic distortion (THD) compared to many techniques. The problem of power ripples in the DPC strategy can be attributed to the use of traditional HC controllers, as these controllers are affected by changes in system parameters, which is undesirable. On the other hand, the reliance of this strategy on estimating powers makes it affected in the event of a malfunction in the machine under study, which is an undesirable matter that contributes to raising the energy/current undulations as well as the THD value[9].

 

In the field of RPs, the quality of current/energy is considered one of the most prominent negatives of the WE system, as the low current quality in the network contributes greatly to increased periodic maintenance, breakdown of electrical machines, costs, and poor operation. Also, reducing the life span of the devices and the energy system itself. Therefore, researchers created several solutions based on the use of the DPC to command the DFIG.

 

The proposed solutions to get rid of the negatives of the DPC depend on the use of smart strategies and nonlinear strategies to compensate for both the HC and ST to command the energies while maintaining the same structure of the traditional DPC strategy, where power estimation is used in these proposed controls. As solutions used, neural networks (NNs)[10], sliding mode command (SMC)[11], backstepping command (BC)[12], synergetic command (SC)[13], adaptive-gain second-order SMC technique[14], proportional-integral (PI) controller[15], predictive control[16], genetic algorithm (GA)[17], fractional-order control[18], and simplified super-twisting control (SSTC)[19] can be mentioned. In all of these solutions, the HC was dispensed with and pulse width modulation (PWM) or space vector modulation was used to command the DFIG inverter. Also, the use of these solutions led to an increase in the performance and effectiveness of the DPC, as this is shown by the results obtained. In these proposed strategies, current/power ripples were reduced very significantly compared to the DPC. But the negative of using these strategies is the complexity, as a significant increase in the degree of complexity is observed compared to the traditional DPC strategy. Also, the use of these solutions, such as nonlinear strategies, increases the number of gains, which makes it difficult to adjust the dynamic response to energy and to obtain good results. Poovathody et al.[20], the author used 12 sectors in the DPC strategy to control induction machine, and twelve sectors HCs were used for this purpose. Accordingly, the resulting command is characterized by robustness, distinguished performance, simplicity, and ease of implementation. In this command, ST was used to control the induction machine inverter, and the MATLAB environment was used to implement it under different working conditions. The simulation results show the high effectiveness of the suggested command due to the use of proposed control, and this is shown by the THD of current and ripple value. In the durability test, it is noted that the proposed command was affected by the change in induction machine parameters, as this effect was less than the effect of the DPC as a result of using capacity estimation. Another drawback of using the proposed technology is that the THD value of current is not significantly reduced, as the proposed strategy is affected by changing machine parameters, which causes a deterioration in the performance and durability of the system. Another DPC strategy was proposed to control the DFIG power in Xiang et al.[21], which represented DPC technique based on SMC. This command is characterized by small number of gains, simplicity, outstanding performance, and high robustness due to the use of an SMC. The designed command is a modification of the DPC, where an SMC was used to compensate for both HC and ST. Therefore, the DPC-SMC has similarities with the DPC in terms of estimation equations, where the same equations are used to estimate energies. Using power estimation makes the suggested command affected by the change in DFIG parameters, which is negative, as the obtained experimental and simulation results show this effect. It is also noted that the suggested command has a higher energy quality than the DPC, which is positive. Bouafia et al.[22], the author used the fuzzy-logic-based switching state selection in order to overcome the disadvantages of the DPC technique of three-phase PWM rectifier, as this strategy was relied upon for its durability and its ability to significantly improve the characteristics of the systems. The outputs of this proposed controller are reference voltage values. These reference values are used to generate the necessary operating pulses, and the PWM strategy is used for this purpose. This proposed command is considered one of the simplest and most easy to apply, as it has a small number of gains, which makes it easy to modify. Also, robustness is one of the most famous features that distinguish it, as the proposed solution does not depend on the mathematical model of the system, which gives it an advantage in the event that the system parameters change. This designed strategy has been verified in MATLAB using several different tests. All test results show the quality of power and current when using designed intelligent regulator compared to a conventional controller. Another solution was used by Antoniewicz et al.[23], where the virtual-flux-based predictive technique was used as an effective solution to defeat the cons of the DPC. The author used a virtual-flux-based predictive technique to control power. This designed technique is characterized by few gains, durability, easy to adjust, low cost, and ease of application. This suggested command was applied to control the AC/DC converters with online inductance estimation, where the PWM was used to produce the pulses necessary to operate the inverter. This virtual-flux-based predictive DPC was verified in the MATLAB using several different tests, where the simulation results showed that the durability and effectiveness are higher in the case of using the suggested controller compared to the DPC and this appears through the minimization rates of power ripples, response time, overshoot, and steady-state error (SSE). Despite this performance, there is a negative characteristic of this strategy, which is affected by changing system parameters, and this appears through the robustness test, which is undesirable. The modified SC strategy was proposed as a suitable solution to ameliorate the characteristic of the DPC of DFIG-MRWT strategy[24], where the modified SC technique was used instead of using HC to command the energy. The PWM was used to operate the DFIG inverter. Therefore, the suggested command is characterized by ease of application, small number of gains, high robustness, simplicity, and low cost compared to several strategies such as the BC. Also, this strategy features a fast dynamic response and this is shown by the simulation results included in all tests. In addition to the dynamic response, it is noted that the use of the proposed strategy led to a significant improvement in the quality of power and current compared to the DPC. The cons of this command lies in its use of power estimation, which makes the power quality decrease in the durability test, which is undesirable. Pura et al.[25], the author used rotor current feedback based on DPC technique of a DFIG operating with unbalanced grid to improve the power characteristics and increase the quality of the current, as the proposed strategy relies on the use of low-voltage ride through, which makes it more durable and performant. This strategy was implemented in a MATLAB environment, where variable wind speed (WS) was used for this purpose. All the results obtained show the high performance of the proposed strategy compared to the traditional strategy. The disadvantage of this strategy lies in its complexity and its reliance on estimating capabilities, which makes it affected if the machine parameters change. Mourad et al.[26], the author used feedback PI controllers to overcome the drawbacks of the DPC of DFIG-MRWT system. The PI feedback controller is characterized by simplicity, robustness, outstanding performance, few gains, and ease of implementation, as it is a modification of the PI regulator only. The PWM was used to operate the DFIG inverter, where power estimation was used to calculate the EE error. The EE error values are inputs to the PI feedback controller and its outputs are voltage reference values. This suggested command was implemented experimentally using dSPACE 1104, where the experimental results performed in the case of two different WS profiles showed that the power quality is better when using the designed controller, which is a positive thing. The experimental results confirm the simulation results obtained with the presence of undulations, as it is not possible to completely eliminate power and current ripples, which is negative. As is known, energy quality and THD value are among the most prominent standards or characteristics that must be paid attention to and an attempt to improve their values in energy systems.

 

In the field of command, other solutions have been designed to defeat the drawbacks of the DPC of the DFIG, which include combining strategies to overcome the cons of the DPC. Merging controls is one of the solutions proposed in recent years in order to address shortcomings and significantly increase the performance of systems, as it is possible to combine two different controls or two similar controls. It is also possible to combine several strategies to obtain a command characterized by high robustness and great effectiveness in amelioration the quality of power and current. Among these solutions that were proposed and used to defeat the cons of the DPC of DFIG, the following are mentioned: BC-SMC[27], dead-beat predictive technique[28], non-linear voltage modulated controller[29], second-order SMC technique[30], SMC-NNs[31], Neuro-fuzzy SMC[32], and neural-STC[33]. In these works, these proposed strategies were used to control powers, where the outputs of these controllers are reference values of voltage. Also, the PWM was mostly used with these controllers to control DFIG. However, these works provided good results in terms of overcoming the cons of the DPC, amelioration the characteristics of the DFIG energy, and increasing its durability. This is shown by the simulation results completed in all tests. Also, it is noted that the THD of current has been significantly minimized, which indicates that the quality of the current has been improved, which is a good thing. But these proposed works have many disadvantages, namely complexity, cost, difficulty of completion, and dynamic response. These strategies mentioned above depend on greatly estimating the power in order to control the generating inverter, which creates large ripples in the durability test, which is undesirable. Yahdou et al.[34], the author used BC technique with nonsingular terminal sliding mode surface (NTSMS) technique to overcome the shortcomings of the DPC of DFIG-MRWT. In this work, the BC technique and NTSMS were combined to obtain a regulator characterized by high durability and great efficiency in minimizing EE undulations and the THD of current, where the PWM was used to operate a generator inverter. This proposed command is characterized by a significant number of gains, which makes it difficult and expensive to adjust. Also, it depends on the MM of the system, which makes it difficult to accomplish and is affected by changing system parameters. All of these negatives mentioned, until in the simulation section, it was noted that this command provided very satisfactory results compared to the DPC and some existing works, and this appears through the comparison completed in terms of undulations reduction rates, response time, THD of current, SSE, and overshoot. Falehi et al.[35], a fractional-order SMC technique based on multi-objective gray wolf optimizer (MOGWO) was applied to ameliorate the energy quality and THD of current of DFIG-based wind turbine. The suggested solution is a combination of several different strategies. Despite the complexity and number of gains that characterized this proposed solution, the simulation results showed that this proposed strategy provided very satisfactory results in all the tests completed and this is shown through the comparison done with the DPC and some works existing in terms of reduction rates. Optimal transition route (OTR) and three-level neutral point clamped were combined in order to defeat the problems of the DPC technique[36], A three-level inverter was used to increase the quality of current and power. This proposed strategy is characterized by great robustness and high efficiency compared to the traditional strategy. This strategy was implemented in MATLAB, where several different tests were used to ensure performance and robustness. Results show the superiority of the suggested command over the DPC and some published papers in terms of ripple minimization ratios, THD of current, overshoot, and SSE. By observing the results of the completed tests, it is found that ripples remain present despite the outstanding performance, which is a negative matter, while noting that the ripples increase in the durability test, which is undesirable. A. Mossa et al.[37], the author proposed a new strategy for DPC of DFIG based on stator voltage-oriented control principle in order to overcome the problems and drawbacks that characterize the traditional strategy. In this work, the author used loss minimization criterion (LMC) in order to determine the reference value for active power, as using the LMC strategy allows obtaining maximum power with great efficiency. Also, in order to increase the robustness of the control strategy, he used a rotor position estimator, as the use of estimating the rotor position allows for improving the performance and effectiveness of the proposed strategy and thus improving the quality of current and power. This proposed strategy was implemented in the MATLAB environment, where the results showed the robustness, performance and efficiency of this proposed strategy compared to the traditional strategy. The negative of this strategy lies in the complexity and difficulty of implementation. Also, its dependence on the mathematical model of the system makes it affected in the event of a malfunction in the system. NNs and the STC were combined to form a controller that features the advantages of both strategies together, with the aim of overcoming the disadvantages of the DPC of DFIG strategy in Adil et al.[38]. This suggested command is characterized by ease of application, simplicity, small number of gains, and high robustness compared to the DPC. Also, this suggested command does not require knowledge of the MM of the system, which makes it greatly affected by changing DFIG parameters. This command uses energy estimation, where the same equations as in the DPC are used. This command was implemented in a MATLAB using VWS, and the results showed the efficiency and ability of the suggested command to significantly improve the system characteristics compared to the DPC. Also, the cons of ripples remains present, especially in the durability test, where it is observed that the value of EE undulations increases, which is negative. Ahmed et al.[39], the author combines dead-beat function and extended kalman filter to overcome cons of the DPC of photovoltaic system. The proposed strategy differs from the traditional strategy in terms of principle and the controller used. But the same estimation equations are used. This proposed strategy is characterized by high performance and great durability with a number of gains. This strategy has the downside of relying on power estimation, which makes it slightly affected if system parameters change. This strategy was implemented using hardware-in-the-loop (HIL) experimental set-up and the results were compared with other strategies. Obtained results prove the high performance of the proposed control in improving the characteristics of the studied system. Almost the same previous work was done in Huang et al.[40], where the author used a combination of fuzzy logic (FL) and SMC technique to ameliorate the performance of the DPC strategy, where the control designed in this work is a modification of the traditional DPC. The combination of the two strategies was relied upon in order to obtain an effective controller to calculate the voltage reference values ​​that are used to generate the necessary pulses. This strategy uses the same estimation equations as the traditional strategy. First, this proposed method was implemented in MATLAB using different tests, with a comparison between the traditional strategy. Secondly, this proposed strategy was implemented experimentally using dSPACE 1104. The results obtained show that the proposed strategy improved the setting time value by an estimated 23% compared to the traditional strategy. Also, the THD of current has been significantly reduced. This strategy has the downside of using FL itself, as there are no mathematical rules that facilitated the application of FL. The latter depends largely on experience in determining the number of rules. Also, the larger the number of rules causes system slowdown which is undesirable. On the other hand, some of the proposed solutions (such as BC-SMC) depend on the MM of the DFIG, which creates cons (ripples) in the event of a malfunction in the system. Therefore, it is necessary to search for another controller that is characterized by low cost, ease of application, few gains, simplicity, and outstanding performance to control DFIG power.

 

In this paper, a novel regulator is designed to overcome the disadvantages of the DPC of DFIG-MRWT, where proportional-dual integral (PDI) controllers based on GA technique are used for this purpose. So, the main contribution of the work is to propose a PDI controller as a solution to improve the current/energy quality of the DFIG-MRWT system. This suggested regulator is characterized by a small number of gains, uncomplicated, easy to implement, fast dynamic response, low cost, and outstanding performance in improving the characteristics of the energy system studied. The second contribution of the work is the use of the DPC-PDI strategy based on GA technique to control DFIG-MRWT. The PDI-GA controller is used to control powers, generating reference voltage values necessary to operate the DFIG inverter of MRWT system. In addition to using PDI-GA, the PWM is used to generate the necessary pulses necessary to operate the RSC of 1500kW DFIG-MRWT. The designed command is a modification of the DPC, as the simplicity, quick dynamic response, and ease of application that characterized the DPC-PI have been preserved. This DPC-PDI-PWM strategy differs from the above-mentioned papers in terms of principle and idea, and is similar to these works in terms of power estimation, where the same equations are used. The behavior of this proposed DPC-PDI-PWM strategy using GA is studied compared to the traditional DPC, and the MATLAB is used for this purpose. A VWS was used to study the behavior of the DPC-PDI-PWM using GA technique, and the necessary numerical and graphical results were extracted. The objectives achieved by this work can be summarized in the following points:

1) Reducing energy undulations to satisfactory proportions compared to the DPC.

2) Significantly increasing the durability of the power system

3) Overcoming the problems of traditional DPC-PI strategy and improving its performance

4) Underestimating the THD of current compared to traditional technique.

5) Underestimating both overshoot and SSE of DFIG power.

 

The sections of the article are as follows: In the second section, the MM of the generator is given. The MM of the turbine used is detailed in Section III. In the fourth section, a detailed explanation of the proposed controller was provided, mentioning the negatives and positives. The proposed strategy for controlling the RSC of DFIG is detailed in Section V. In the sixth section, simulation of the proposed strategy is discussed, comparing the numerical and graphical results obtained with the DPC. Finally, the article ends with a section in which the main results obtained from the work completed are listed.

 

2 METHODS AND MODELS

2.1 DFIG Model

The DFIG is considered one of the most famous electric generators in the field of renewable energies, especially in the field of variable WS, due to the advantages it has compared to other types[10]. This generator has an advantage that is not found in other machines, as the resulting power can be regulated by feeding the rotating part of the DFIG, which allows changing the resulting energy. Therefore, two different inverters are used to feed the rotating part of the machine, and two different or similar controls are used to control the two inverters[2,3]. DFIG is also characterized by ease of control, low cost, high durability, and low maintenance, which makes it most suitable for this study[13,14]. It is necessary to know the MM of DFIG to simulate the proposed energy system, and Equations (1)-(4) are used for this purpose.

 

The expressions of the Ps and Qs delivered from the DFIG are given by Mohammedi et al.[2] and Yessef et al.[4]:

 

 

The rotating part of the machine can be represented by Equation (2), and based on this equation, the operation of the DFIG can be controlled. Depending on the value of the difference in torque, operation and power generation are controlled[39,40].

 

 

where, Te is the DFIG torque and Tch is the MRWT torque[35,37].

 

 

where, Iqr, Idr, Iqs, and Ids are the rotor and stator currents in the d-q reference frame;

ϕqr, ϕdr, ϕqs, and ϕds are rotor and stator flux in the d-q reference frame;

Vqr, Vdr, Vqs, and Vds are the rotor and stator voltages in the d-q reference frame;

The stator and rotor angular velocities are linked by the following relation ωs=ωm+ωr;

Rr and Rs are respectively the resistances of the rotor and stator windings;

M, Lr, and Ls are respectively the mutual inductance, the inductance on the rotor and the inductance on the stator;

ωr is the electrical pulsation of the rotor and ωsis the stator one, while ωm is the mechanical pulsation of the DFIG.

 

Equation (4) shows the DFIG torque Te[34,38].

 

 

2.2 MRWT Model

MRWT is one of the technologies that have recently appeared in the field of REs as a suitable solution for generating EE from wind, as these turbines are considered more effective than traditional turbines in terms of the value of the energy gained from the WE. These turbines generate power estimated at 20% to 35% times greater than the power gained from the WE using traditional turbines[41]. These turbines have been studied in several papers[42-45], and all of these papers confirm the effectiveness and performance of these turbines. According to the work done in MRWT[46], it is two turbines combined together to form a single turbine, where several turbines can be used for this purpose. The use of these turbines greatly helps reduce the area of WE farms and thus reduce costs. In addition, the use of these turbines in wind farms greatly contributes to overcoming the wind generated between the turbines, which makes the turbines have a high yield compared to traditional turbines[47]. The cons of these turbines lies in their high costs and the presence of a significant number of mechanical parts, which makes them difficult to maintain and has high costs. Compared to ordinary turbines, this technology is difficult to control, and the MPPT strategy is used for this purpose. In Equation (5) both the torque and power generated by the MRWT are shown[43,44].

 

 

In MRWT, the resulting torque value is related to the WS before and after the main turbine, as each turbine has its own torque. The two turbines used have two different capacities, as one turbine with large dimensions and another with small dimensions are used Ullah et al., Ullah et al.[43,46]. In Equation (6) the two turbine torques are shown Benbouhenni et al. [47].

 

 

where, R1 and R2 are the blade radius of the two sub-turbines, Cp is power coefficient, T1 and T2 represent the torque produced by the two sub-turbines, λ1 and λ2 are the tip speed ration of the two sub-turbines, and ρ is the air density.

 

In Equation (7), the power coefficient is clarified, which is of very great importance, as its value is related to the power gained from the WE, where the larger its value, the greater the energy value.

 

where, β is the pitch angles.

 

Each turbine formed for the MRWT has its own tip speed ratio, and the Equation (8) can be used to determine the ratio of speed for each turbine[41,47].

 

As is known, in MRWT the WS of the turbines varies from one turbine to another, where the WS before the turbine 1 (V1) is the normal WS, and in the case of the turbine 2 the WS is calculated using Equation (9). This speed is related to the distance between the two turbines and a fixed factor (CT) that takes the value of 0.9[42,46].

 

 

2.3 Proposed PDI Controller

The PI is considered one of the most famous and widely used regulators in several different fields because of its simplicity and ease of application[15]. Also, it has a low cost and fewer gains, allowing the dynamic response to be easily tuned. Its use in the field of control gives a fast dynamic response, which is good and desirable. This regulator can be expressed by Equation (10).

 

 

In the field of command, the use of a PI controller creates several cons and defects in the systems, as this controller is greatly affected by changing the values of the DFIG parameters, which is undesirable. Several solutions have been designed to overcome this problem. The PI (1+PI) controller was used in Habib et al.[48] to overcome defects and problems, as this controller is characterized by simplicity and distinguished performance. However, this suggested controller has a drawback in the form of a significant number of gains. Benbouhenni et al.[49], a proportional-derivative controller (1+PI) was proposed to overcome the problems of the DPC, as this regulator was designed to compensate for the use of the PI. However, this regulator has disadvantages, namely the large number of gains compared to the PI and the response time, as it provided a response time to capabilities greater than the PI controller. The results showed that the proposed regulator is superior to the PI in terms of durability and ameliorating the performance of the energy system. Zellouma et al.[50], it was proposed to use two PI controllers in parallel to defeat the cons of the PI to command the asynchronous motor. The suggested controller is complex compared to the PI controller and contains a significant number of gains. Also, the proposed controller is expensive and difficult to implement. Despite these drawbacks, the results showed the high effectiveness of this proposed controller compared to the PI controller in terms of reducing current and torque ripples. Also, in terms of reducing the value of THD of current and the response time of flux and torque.

 

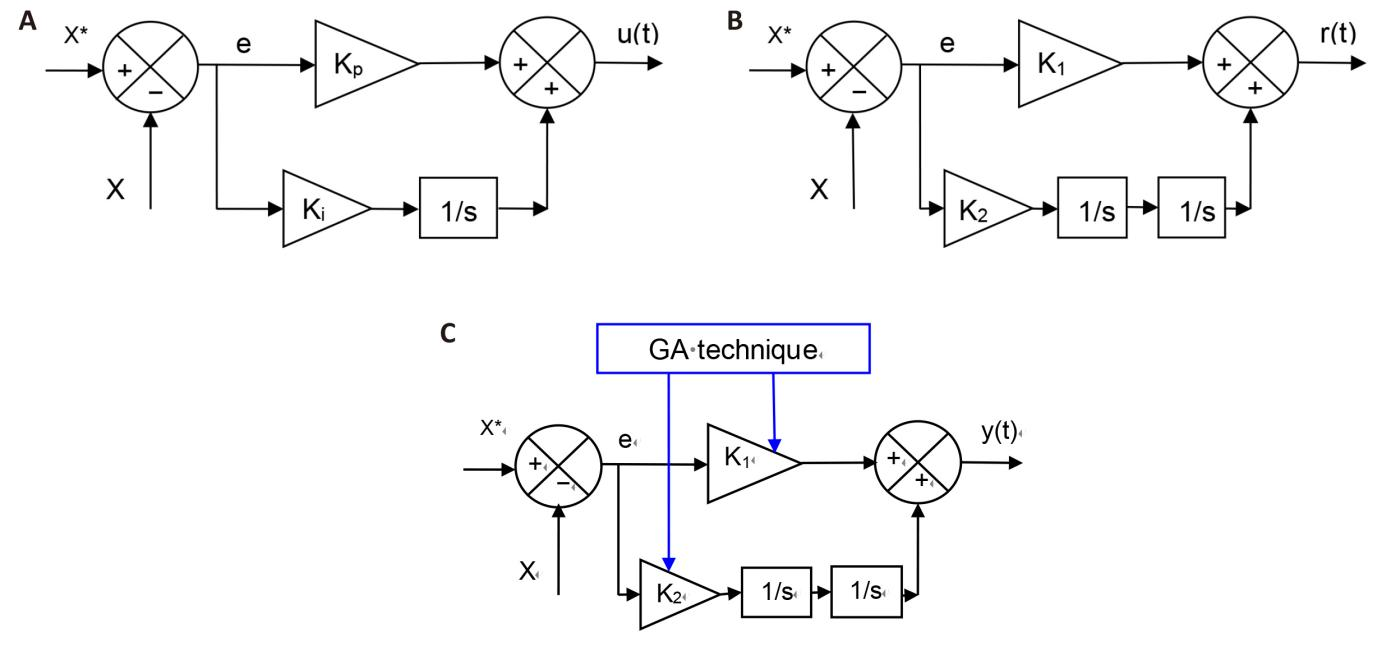
In this part, a solution different from the aforementioned solutions is proposed to defeat the cons of the PI, and the use of PDI is proposed for this purpose. So the PDI controller is a different controller from the PI controller in principle, as two integrators are used in series for this purpose. The PDI controller is a variation of the traditional controller and therefore they have the same number of gains. Equation (11) shows the MM of the PDI controller used in this work.

 

 

where, K1 and K2 are the gains of the proposed controller. By means of these gains the response is adjusted and changed. The designed controller is characterized by ease of application and simplicity with a lower cost, as it can be accomplished using dSPACE 1104 with ease. The parameters of this proposed controller are calculated in this work using the GA strategy, as using this strategy leads to increased performance, robustness, and efficiency in overcoming the defects of the DPC strategy.

 

Figure 1 represents the proposed regulator and the PI, as it is noted that they have almost the same structure.

 

Figure 1. The proposed PDI controller. A: PI controller; B: PDI controller; C: PDI-GA controller.

 

The proposed PDI controller based on GA technique is used as an effective solution to overcome the cons of the DPC of 1,500kW DFIG-MRWT, as in the next part the necessary and essential details of the DPC-PDI-PWM are mentioned.

 

2.4 Proposed DPC-PDI-PWM Strategy

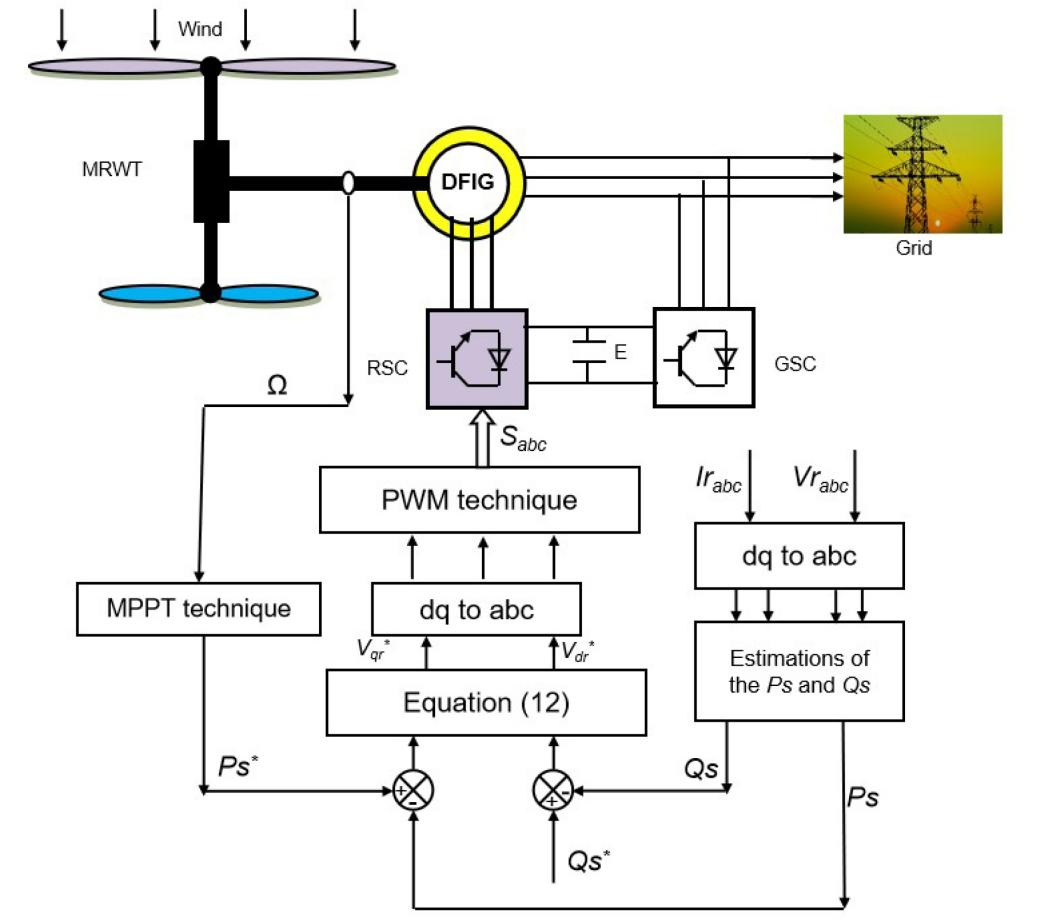
In this part, the necessary details of the proposed strategy, which is DPC-PDI-PWM technique based on GA technique, are given. This command is different from the DPC in terms of principle, idea, complexity, durability, performance, and cost. In the proposed DPC-PDI-PWM strategy based on GA, the PWM is used to replace the ST to produce the pulses needed to operate the RSC. Also, two PDI-GA controllers are used to control powers, as these two proposed controllers are used to generate voltage reference values. The latter is used to produce the impulses necessary to operate the RSC. The use of the GA technique was chosen for its ease and simplicity. This strategy does not require a specialist, as it provides good results.

 

In the DPC-PDI-PWM strategy, power estimation is used to obtain the energy error, and these errors are used in calculating the voltage reference values. Figure 2 represents the architecture of the DPC-PDI-PWM used in this work to command an power system based on MRWT. The MPPT is used for the purpose of calculating the reference value for Ps, and this reference value is used to determine the Ps error. Therefore, using the MPPT strategy makes the value of the Ps related to the shape of the WS, as when the WS increases, the value of the Ps increases with it, and vice versa. The proposed strategy requires estimating capabilities, as the same energy estimation equations found in the DPC are used. Using power estimation requires measuring voltage and current. Therefore, the flux must be estimated first before estimating capacities, as estimating capacities is linked to estimating flux.

 

In the DPC-PDI-PWM strategy, a PDI control is used to produce the reference values (Vdr* and Vqr*), and the Equation (11) is used for this purpose. So, to produce the voltage reference values, the following equation is used:

 

 

where, ePs and eQs are the errors of Ps and reactive power (Qs).

 

Equation (13) can be used to calculate the quadrature and direct fluxes[2,3].

 

 

where, Vsα and Vsβ are the voltage linkage of α-β axis.

Ψrβ is the flux linkage of β-axis, Lm is the mutual inductance, Ѱrα is the rotor flux linkage of α-axis. with:

 

Figure 2. Proposed technique of DFIG-MRWT system.

 

 

The angle between Ψsβ and Ψsα is given by Equation (15)[17,18].

 

 

In Equation (16), the relationship between voltage and flux is given, where it is noted that flow increases with increasing voltage and vice versa[27].

 

 

where, Vs is the voltage.

 

Using the flux estimation equations mentioned above, capacities can be estimated using Equation (17)[13,19], as this equation is the same DPC equation. Through this equation, it is noted that the change in power is related to the change in flux, and since the flux is related to the change in voltage, the power is related to the change in voltage.

 

 

 

3 RESULTS

In this part, a simulation of the DPC-PDI-PWM based on GA technique is performed compared to the traditional strategy (DPC-PI), and the MATLAB is used for this purpose. The system parameters used are as follows: fs=50Hz, Rs=12mΩ, Ls=13.7mH, 380/696V, Lr=13.6mH, Lm=13.5mH, Rr=21mΩ, J=1000kgm2, p=2, and fr=0.0024Nm/s[17,29].

 

The necessary numerical and graphical results are extracted to show the performance and robustness of the DPC-PDI-PWM based on GA technique, and various tests are used for this purpose. In order to study the behavior of the DPC-PDI-PWM based on GA technique, a variable WS is used.

 

The parameters of the system proposed in this work are listed in Table S1. Also, the model was given in the MATLAB environment for the proposed system to illustrate the work done (See Figure S1).

 

3.1 First Test

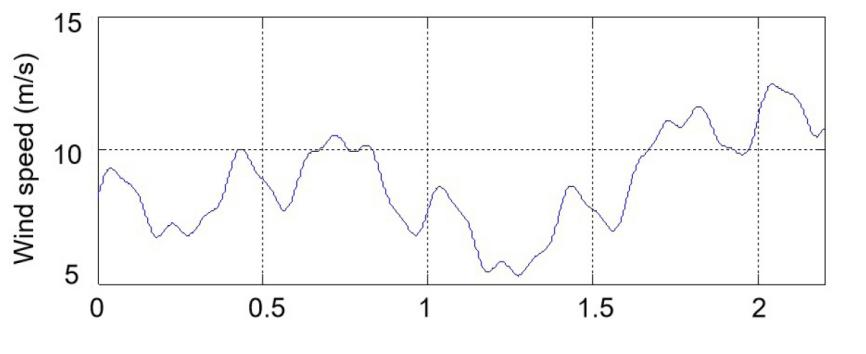
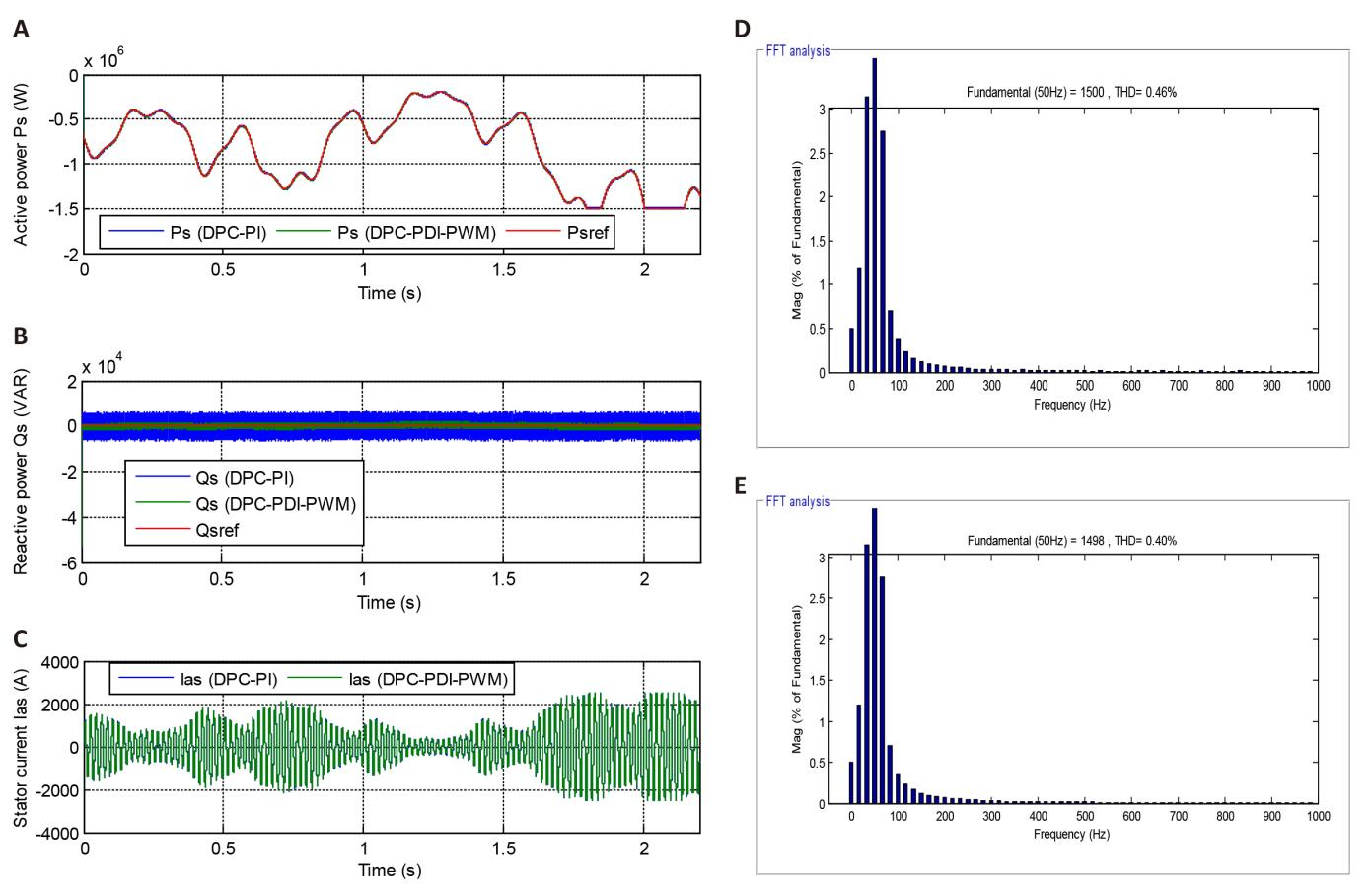
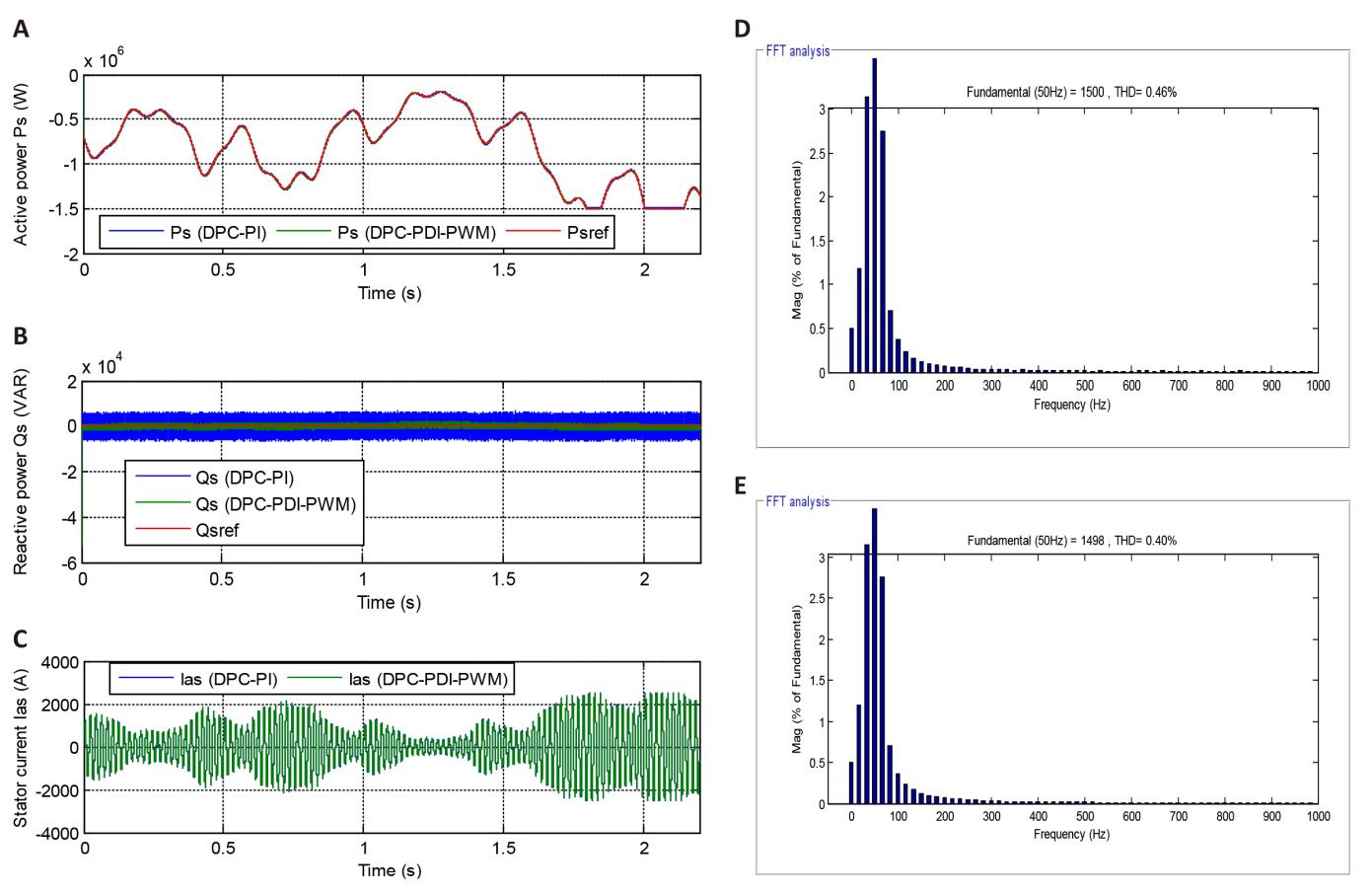
In this test, the WS represented in Figure 3 is used to study the behavior of the proposed DPC-PDI-PWM strategy based on GA technique, where the graphical results are represented in Figure 4. This figure gives a clear picture of the change in the behavior of power compared to a change in VWS, as Ps is greatly affected by a change in WS (Figure 4A). Ps increases with increasing VWS and decreases with decreasing VWS. However, the Qs is not affected by the change in VWS throughout the simulation period, as it remains constant and takes a zero value in the presence of undulations (Figure 4B).

 

Figure 3. WS profile.

 

The current is represented in Figure 4C for the two controls, where it is noted that the shape of the current takes a sinusoidal shape. The value of the current is related to the change in VWS, as its value increases with increasing WS and decreases with its decrease, with the DPC-PDI-PWM technique having an advantage in terms of quality compared to the DPC-PI. The THD of current for the two commands is represented in Figure 4D and 4E, where it is noted that the value of THD was 0.46% and 0.40% for both the DPC-PI and the DPC-PDI-PWM, respectively. So, the DPC-PDI-PWM reduced the THD compared to the DPC-PI, as the minimization percentages was estimated at 13.04%, which is desirable and indicates that the DPC-PDI-PWM technique provided satisfactory performance compared to the DPC-PI. It is also noted that the amplitude value of the fundamental of current signal (FCS) was 1500A and 1498A for DPC-PI and DPC-PDI-PWM, respectively. Therefore, the DPC-PI provided a larger amplitude than the amplitude provided by the DPC-PDI-PWM, which makes it said that the amplitude of the FCS is negative for the DPC-PDI-PWM.

 

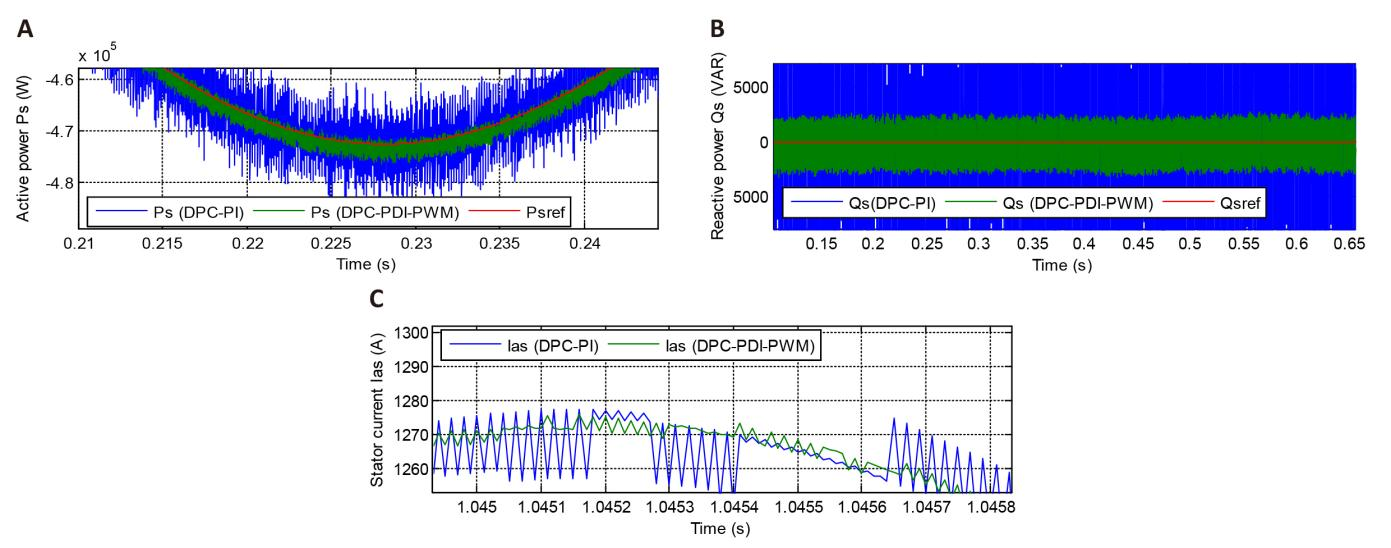
Figure 5 represents the zoom in the results of the first test. This figure shows that the ripples of both power and current are significantly reduced in the DPC-PDI-PWM technique compared to the DPC-PI, where the undulations values and minimization percentages are given in Table 1.

 

Figure 4. First test results. A: Active power; B: Reactive power; C: Stator current; D: THD (DPC-PI); E: THD (DPC-PDI-PWM).

 

Figure 5.  Zoom (first test). A: Active power; B: Reactive power; C: Stator current.

 

Table 1. Ratios/Values of SSE, Ripples, RT, and Overshoot in the FirstTest Case

 

The numerical results are shown in Table 1, where the values and ratios of RT, overshoot, ripples, and SSE of DFIG power are given. From this table it is noted that the DPC-PDI-PWM technique provided better results in terms of overshoot, undulations, and SSE compared to the DPC-PI, this is shown through the calculated ratios. The DPC-PDI-PWM reduced the values of ripple, SSE, and overshoot of Ps by ratios estimated at 83.10%, 89.35%, and 71.91%, respectively, compared to the DPC-PI strategy. Also, overshoot, ripples, and SSE of Qs were reduced by 79.09%, 79%, and 70.68% compared to the DPC-PI. However, this DPC-PDI-PWM technique has a negative side, represented by the RT, as it provided an unsatisfactory time for DFIG power compared to the DPC-PI, which is undesirable.

 

3.2 Second Test

In this test, the behavior of the DPC-PDI-PWM is studied in terms of robustness, and the machine parameters are changed for this purpose. Resistance values are multiplied by 2 and coil values are multiplied by 0.5. In this test, the same WS used in the first test is used, and the graphical results obtained are represented in Figure 6. The latter shows that the capabilities follow the references well despite the change in the DFIG parameters. The Ps changes according to the change in VWS, and the Qs remains constant and does not change, although larger undulations are observed in the DPC-PI. Also, the current takes a sinusoidal shape in this test for the two controls, as its value changes according to the change in VWS. Figure 6D and 6E represent the THD for the two commands, where the THD was 1.65% and 1.56% for the DPC-PI and DPC-PDI-PWM techniques, respectively. Accordingly, the proposed DPC-PDI-PWM strategy reduced the THD value by an estimated rate of 5.45%, as this percentages shows that the current quality is better in the DPC-PDI-PWM compared to the DPC-PI. Also, it is noted that the two controls provided almost the same amplitude for the FSC, which is a good thing for the DPC-PDI-PWM, as the amplitude value was 917.5A and 917.4A for both the DPC-PI and the DPC-PDI-PWM strategy, respectively.

 

Figure 6. Second test results. A: Active power; B: Reactive power; C: Current; D: THD (DPC); E: THD (DPC-PDI-PWM).

 

According to Figure 7, the ripples of both current and DFIG power are low when using the DPC-PDI-PWM technique compared to the DPC-PI, which is a good thing that shows the high effectiveness of the DPC-PDI-PWM in improving the performance of the studied DFIG-MRWT.

 

Figure 7. Zoom in the second test results. A: Active power; B: Reactive power; C: Current.

 

The numerical results of the second test are represented in Table 2, where the values and percentages of minimization of ripples, RT, SSE, and overshoot of DFIG power are given. The DPC-PDI-PWM technique provided lower values for overshoot, undulations, and SSE of DFIG power compared to the DPC-PI, and this appears through the high percentages, which indicates the distinctive and effective performance in improving the system characteristics. The DPC-PDI-PWM strategy reduced ripple, SSE, and overshoot of Qs by ratios estimated at 76%, 84.84%, and 84.84%, respectively, compared to the DPC-PI strategy. Also, the SSE, ripples, and overshoot of Ps were minimized by ratios estimated at 71.72%, 87%, and 62.50%, respectively, compared to the DPC-PI. These high percentages demonstrate the efficiency/effectiveness of the DPC-PDI-PWM in improving the system characteristics despite changing the DFIG-MRWT parameters. The negative of the DPC-PDI-PWM technique lies in the RT, as it provided an unsatisfactory time for DFIG energy compared to the DPC-PI, which is an undesirable matter that can be overcome by adding intelligent techniques such as GA techniques to determine the DPC-PDI-PWM parameters.

 

Table 2. Ratios/Values of SSE, Overshoot, Ripples, and RT inthe Second Test Case

 

In Table 3, the change in the THD is studied. It is noted that the THD was greatly affected in the test 2 compared to the first test as a result of changing the DFIG parameters. Accordingly, the percentages of change was estimated at 72.12% and 74.35% for both the DPC-PI and DPC-PDI-PWM, respectively. So the DPC-PI provided a lower percentages than the DPC-PDI-PWM technique, even thought the THD value was high in the DPC-PI compared to the DPC-PDI-PWM technique. In Table 4, the change in the amplitude of the fundamental signal of current in the first and second tests is studied. It is noted that the amplitude value decreased significantly in the test 2 compared to the test 1 for the two commands due to the change in the DFIG parameters. Therefore, the amplitude of the fundamental signal is affected by changing system parameters, as this effect was estimated at 38.85% and 38.75% for both the DPC-PI and the DPC-PDI-PWM, respectively. The DPC-PDI-PWM strategy is less affected than the DPC-PI strategy, which is a positive thing.

 

Table 3. Study of the Change in THD Value in the Two Tests

 

Table 4. Study of the Change in Amplitude of Fundamental Signal of Current in the Two Tests

 

3.3 Third Test

In this test, the DPC-PDI-PWM strategy is studied using the VWS represented in Figure 8, where graphical results are represented in Figure 9 and numerical results are listed in Table 5.

 

Figure 8. Steps WS profile.

 

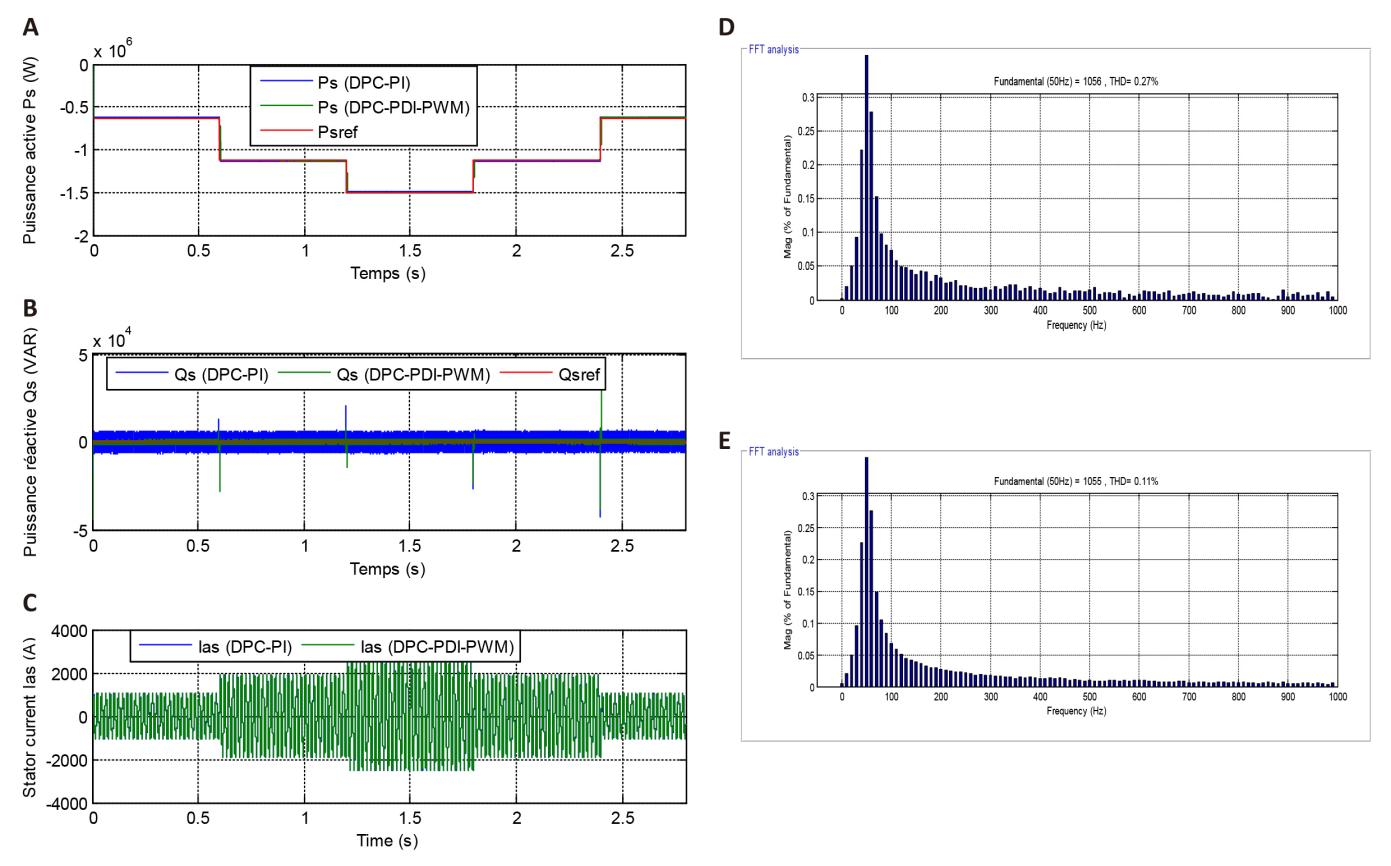
In Figure 9, the capacities follow the references well, with larger undulations in the case of using the DPC-PI. Compared to the DPC-PDI-PWM strategy. Also, the change in Ps is the same as the change in VWS as a result of using MPPT to calculate the reference value. But the Qs is not affected by the change in WS and remains constant and non-existent.

 

Figure 9C represents the current for the two commands, where the current changes according to the change in WS and takes a sinusoidal shape with ripples. The value of a current increases and decreases with increasing and decreasing WS.

 

The THD of current is represented in Figures 9D and 9E, where it was 0.27% and 0.11% for both the DPC-PI and the DPC-PDI-PWM, respectively. Accordingly, the DPC-PDI-PWM minimized the THD significantly compared to the DPC-PI, as this minimization was estimated at a rate of 59.25%. Also, the DPC-PI gave a larger FCS than the DPC-PDI-PWM. This amplitude was 1056A and 1055A for both the DPC-PI and DPC-PDI-PWM, respectively. So, it can be said that the negativity of the DPC-PDI-PWM in this test is the amplitude of the FCS.

 

Figure 9. Third test results. A: Active power; B: Reactive power; C: Current; D: THD (DPC); E: THD (DPC-PDI-PWM).

 

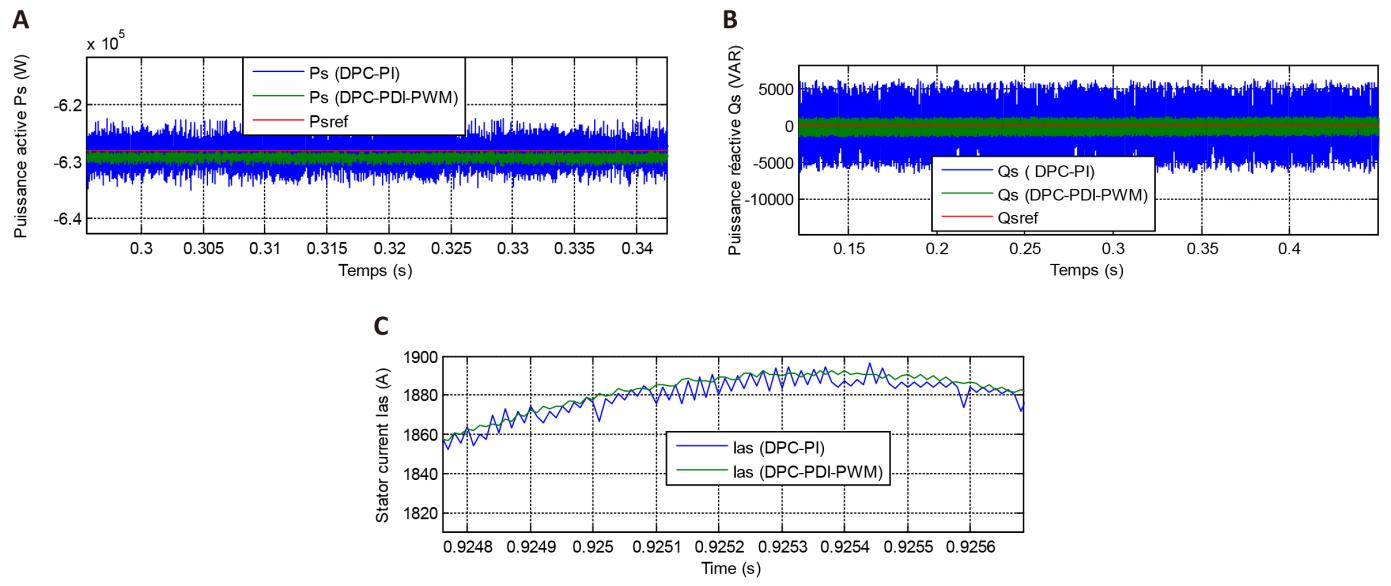
Figure 10 shows the superiority of the DPC-PDI-PWM in terms of undulations compared to the DPC-PI. Accordingly, the DPC-PDI-PWM minimized the undulations of both power and current significantly compared to the DPC-PI, which is a positive thing that shows the superiority of this command.

Figure 10. Zoom in the third test results. A: Active power; B: Reactive power; C: Current.

 

The numerical values of this test are represented in Table 5 for the two controls, where it is noted that the DPC-PDI-PWM provided satisfactory and unsatisfactory results compared to the DPC-PI. The DPC-PDI-PWM minimized the values of ripple, overshoot, and SSE of Ps by percentages estimated at 84.07%, 89.09%, and 61.53%, respectively. Both ripples and SSE of Qs were reduced by 78.98% and 79.85%, respectively, compared to the DPC-PI. The DPC-PDI-PWM provided unsatisfactory results in terms of response time to power compared to the DPC-PI. The latter reduced RT by rates estimated at 69.42% and 69.93% for both Ps and Qs, respectively, compared to the DPC-PDI-PWM. Also, the DPC-PI strategy gave satisfactory results for overshoot of Qs compared to the DPC-PDI-PWM, where the minimization percentage was estimated at 82.53%.

 

Table 5. Ratios/Values of ripples, Overshoot, SSE, and RT in the Third Test Case

 

In Tables 6 and 7, the effect of the amplitude of the FCS and the THD value for the two commands is studied, as it is noted that the THD was affected by changing the shape of the WS. The THD value was lower in the third test compared to the first test for the two commands, where this decrease was estimated at 41.30% and 72.50% for both the DPC-PI and the DPC-PDI-PWM strategy, respectively. Therefore, the DPC-PDI-PWM strategy provided a greater percentage, which indicates its higher performance in reducing the value of THD compared to the DPC-PI strategy. Also, the amplitude of the FCS decreased significantly in the third test for the two controls compared to the first test. This decrease was estimated at 29.60% and 29.57% for both the DPC-PI and DPC-PDI-PWM, respectively. Therefore, it can be said that the shape of the WS change has a direct effect on the value of both the amplitude of the FCS and the value of the current THD.

 

Table 6. Study of the Change in THD Value in the First and Third Tests

 

Table 7. Study of the Change in Amplitude of Fundamental (50Hz) Signal in the First and Third Tests

 

The proposed DPC-PDI-PWM strategy has effective performance in terms of THD value of current (see Table 8), reduction of power ripples (see Table 9), and SSE value reduction ratios for powers (see Table 10) compared to several research papers. So, the proposed DPC-PDI-PWM strategy has the ability to significantly improve the quality of current and power compared to several strategies, which makes it a suitable and reliable solution, and this is shown in Tables 8, 9, and 10. This completed comparison gives a clear picture that the proposed DPC-PDI-PWM strategy can compensate for several existing controls in the field of control. Which is a positive thing.

 

Table 8. Comparing the DPC-PDI-PWM and Some Existing Papers in Terms of the THD

 

Table 9. Comparison in Terms of Energy Ripple Reduction Rates

 

Table 10. Comparison in Terms of SSE for Qs and Ps

 

4 CONCLUSIONS

In this study, a new control was proposed that is characterized by ease of application and simplicity with distinctive and effective characteristic in order to improve the energy/current quality. The DPC-PDI-PWM technique was used to control the RSC of 1.5MW DFIG-MRWT, where the MATLAB was used for this purpose. Two different tests were used to study the DPC-PDI-PWM technique behavior compared to the DPC-PI. In the DPC-PDI-PWM, an GA was used to calculate the parameters of the regulator used to control the power. So, according to the obtained graphical and numerical results, the DPC-PDI-PWM provided very satisfactory results, as it significantly reduced energy and current ripples. Also, the DPC-PDI-PWM technique underestimates the SSE and overshoot of DFIG power compared to the DPC-PI. The presented results demonstrate the superiority of the DPC-PDI-PWM in terms of THD value compared to the DPC-PI. The THD for the two commands changed from the first test to the second test, as it is noted that the DPC-PI provided a greater value compared to the DPC-PDI-PWM technique. However, the rate of change in the THD value was greater in the DPC-PDI-PWM technique compared to the DPC-PI, which is undesirable. The completed work was restricted to using only a VWS, and in the future this work will be studied using other tests, for example, a network error. In the future, this paper will be carried out experimentally and the results obtained will be confirmed by simulation, along with the implementation of other strategies that are more effective in improving the characteristics of the energy system based on MRWT.

 

Acknowledgements

Not applicable.

 

Conflicts of Interest

The author declares no conflict of interest.

 

Author Contribution

Benbouhenni H conceptualized and designed the proposed power system, supervised the work, conducted data analysis, and drafted the manuscript. The author contributed to writing the article, read, and approved its submission.

 

Abbreviation List

BC, Backstepping control

DFIG, Doubly-fed induction generator

DPC, Direct power control

DTC, Direct torque control

EE, Electrical energy

GA, Genetic algorithm

HC, Hysteresis comparator

MPPT, Maximum power point tracking

MRWT, Multi-rotor wind turbine

NNs, Neural networks

PDI, Proportional dual integral

PI, Proportional-integral controller

Ps, Active power

PWM, Pulse width modulation

RPs, Renewable powers

SMC, Sliding mode control

SSE, Steady-state error

SSTC, Simplified super-twisting control

ST, Switching table

THD, Total harmonic distortion

VWS, Variable wind speed

WE, Wind energy

WS, Wind speed

 

References

[1] Yousefi-Talouki A, Zalzar S, Pouresmaeil E. Direct Power Control of Matrix Converter-Fed DFIG with Fixed Switching Frequency. Sustainability, 2019; 11: 2604.[DOI]

[2] Mohammadi J, Vaez-Zadeh S, Afsharnia S et al. A Combined Vector and Direct Power Control for DFIG-Based Wind Turbines. IEEE Trans Sustain Energ, 2014; 5: 767-775.[DOI]

[3] Mazen Alhato M, Bouallègue S, Rezk H. Modeling and Performance Improvement of Direct Power Control of Doubly-Fed Induction Generator Based Wind Turbine through Second-Order Sliding Mode Control Approach. Mathematics, 2020; 8: 2012.[DOI]

[4] Han Y, Ma R. Adaptive-Gain Second-Order Sliding Mode Direct Power Control for Wind-Turbine-Driven DFIG under Balanced and Unbalanced Grid Voltage. Energies, 2019; 12: 3886.[DOI]

[5] Datta R, Ranganathan V. Direct power control of grid-connected wound rotor induction machine without rotor position sensors. IEEE Trans Power Electron, 2001; 16: 390–399.[DOI]

[6] Alizadeh O, Yazdani A. A Strategy for Real Power Control in a Direct-Drive PMSG-Based Wind Energy Conversion System. IEEE Trans Power Deliv. 2013; 28: 1297-1305.[DOI]

[7] Djazia K, Krim F, Chaoui A et al. Active Power Filtering Using the ZDPC Method under Unbalanced and Distorted Grid Voltage Conditions. Energies, 2015; 8: 1584-1605.[DOI]

[8] Sayeh KF, Tamalouzt S, Sahri Y. Improvement of power quality in WT-DFIG systems using novel direct power control based on fuzzy logic control under randomness conditions. Int J Model Simul, 2023; 1-13.[DOI]

[9] Aroussi HA, Ziani E, Bouderbala M et al. Enhancement of the direct power control applied to DFIG-WECS. Int J Electr Comput Eng. 2020, 10: 35.[DOI]

[10] Chojaa H, Derouich A, Chehaidia SE et al. Enhancement of Direct Power Control by Using Artificial Neural Network for a Doubly Fed Induction Generator-Based WECS: An Experimental Validation. Electronics, 2022; 11: 4106.[DOI]

[11] Shang L, Hu J. Sliding-Mode-Based Direct Power Control of Grid-Connected Wind-Turbine-Driven Doubly Fed Induction Generators Under Unbalanced Grid Voltage Conditions. IEEE Trans Energ Conver, 2012; 27: 362-373.[DOI]

[12] Xiong P, Sun D. Backstepping-Based DPC Strategy of a Wind Turbine-Driven DFIG Under Normal and Harmonic Grid Voltage. IEEE Trans Power Electr, 2016; 31: 4216-4225.[DOI]

[13] Ardjal A, Bettayeb M, Mansouri R et al. Nonlinear synergetic control approach for dc-link voltage regulator of wind turbine DFIG connected to the grid. 2018 5th International Conference on Renewable Energy: Generation and Applications (ICREGA), IEEE, 2018: 94-97.[DOI]

[14] Han Y, Ma R. Adaptive-Gain Second-Order Sliding Mode Direct Power Control for Wind-Turbine-Driven DFIG under Balanced and Unbalanced Grid Voltage. Energies 2019; 12: 3886.[DOI]

[15] Zoghlami M, Kadri A, Bacha F. Analysis and Application of the Sliding Mode Control Approach in the Variable-Wind Speed Conversion System for the Utility of Grid Connection. Energies, 2018; 11: 720.[DOI]

[16] Wang X., Sun D. Three-Vector-Based Low-Complexity Model Predictive Direct Power Control Strategy for Doubly Fed Induction Generators. IEEE Trans Power Electr, 2017; 32: 773-782.[DOI]

[17] Samira D, Abdelhafid S, Mohamed K et al. Genetic algorithm optimization of a SAPF based on the fuzzy DPC concept, Przegląd Elektrotechniczny, 2019; 7: 60-65.[DOI]

[18] Afghoul H, Krim F, Chikouche D et al. Fractional direct power control for active filter. 2013 IEEE 7th International Power Engineering and Optimization Conference (PEOCO). IEEE, 2013: 228-233.[DOI]

[19] Debdouche N, Deffaf B, et al. Direct Power Control for Three-Level Multifunctional Voltage Source Inverter of PV Systems Using a Simplified Super-Twisting Algorithm. Energies, 2023; 16: 4103.[DOI]

[20] Poovathody A, Ramchand R. Twelve Sector Based Direct Power Control of Induction Motor Drives. 2020 International Conference on Power Electronics and Renewable Energy Applications (PEREA), IEEE, 2020: 1-5.[DOI]

[21] Xiong L, Li P, Li H et al. Sliding Mode Control of DFIG Wind Turbines with a Fast Exponential Reaching Law. Energies, 2017; 10: 1788.[DOI]

[22] Bouafia A, Krim F, Gaubert JP. Fuzzy-logic-based switching state selection for direct power control of three-phase PWM rectifier. IEEE Trans Ind Electron, 2009; 56: 1984-1992.[DOI]

[23] Antoniewicz P, Kazmierkowski MP. Virtual-flux-based predictive direct power control of AC/DC converters with online inductance estimation. IEEE Trans Ind Electron, 2008; 55: 4381-4390.[DOI]

[24] Benbouhenni H, Bizon N, Colak I et al. Direct active and reactive powers control of double-powered asynchronous generators in multi-rotor wind power systems using modified synergetic control. Energy Rep, 2023; 10: 4286-4301.[DOI]

[25] Pura Pl Iwański G. Rotor Current Feedback Based Direct Power Control of a Doubly Fed Induction Generator Operating with Unbalanced Grid. Energies, 2021; 14: 3289.[DOI]

[26] Mourad Y, Benbouhenni H, Taoussi M et al. Experimental validation of feedback PI controllers for multi-rotor wind energy conversion systems. IEEE Access, 2024; 12: 7071-7088.[DOI]

[27] Echiheb F, Ihedrane Y, Bossoufi B et al. Robust sliding-Backstepping mode control of a wind system based on the DFIG generator. Sci Rep, 2022; 12: 11782.[DOI]

[28] Hu J. Improved Dead-Beat Predictive DPC Strategy of Grid-Connected DC–AC Converters With Switching Loss Minimization and Delay Compensations. IEEE Trans Ind Infor, 2013: 728-738.[DOI]

[29] Cheng P, Wu C, Ning F et al. Voltage Modulated DPC Strategy of DFIG Using Extended Power Theory under Unbalanced Grid Voltage Conditions. Energies, 2020; 13: 6077.[DOI]

[30] Alhato MM, Bouallègue S, Rezk H. Modeling and Performance Improvement of Direct Power Control of Doubly-Fed Induction Generator Based Wind Turbine through Second-Order Sliding Mode Control Approach. Mathematics, 2020; 8, 2012.[DOI]

[31] Ouada L, Benaggounea S., Belkacemb S. Neuro-fuzzy Sliding Mode Controller Based on a Brushless Doubly Fed Induction Generator. Int J Eng, 2020; 33: 248-256.[DOI]

[32] Ahmad K, Hamed T, Zahra SS. ANFIS based sliding mode control of a DFIG wind turbine excited by an indirect matrix converter. Int J Power Electr Drives Syst, 2023; 14: 1739-1747.[DOI]

[33] Sami I, Ullah S, Amin SU et al. Convergence Enhancement of Super-Twisting Sliding Mode Control Using Artificial Neural Network for DFIG-Based Wind Energy Conversion Systems. IEEE Access, 2022; 10: 97625-97641.[DOI]

[34] Yahdou A, Benbouhenni H, Colak I et al. Application of Backstepping Control With Nonsingular Terminal Sliding Mode Surface Technique to Improve the Robustness of Stator Power Control of Asynchronous Generator-Based Multi-Rotor Wind Turbine System. Electr Pow Compo Sys, 2024; 0:1-29.[DOI]

[35] Falehi AD. Optimal Power Tracking of DFIG-Based Wind Turbine Using MOGWO-Based Fractional-Order Sliding Mode Controller. J. Sol. Energy Eng. 2020; 142, 1–35.[DOI]

[36] Hamed HA, Abdou AF, Moursi MSE et al. A Modified DPC Switching Technique Based on Optimal Transition Route for of 3L-NPC Converters. IEEE Trans Power Electron, 2018; 33: 1902-1906.[DOI]

[37] Mossa MA, Echeikh H, Diab AAZ et al. Effective Direct Power Control for a Sensor-Less Doubly Fed Induction Generator with a Losses Minimization Criterion. Electronics 2020; 9, 1269.[DOI]

[38] Yahdou A, Djilali AB, Bounadja E et al. Using neural network super-twisting sliding mode to improve power control of a dual-rotor wind turbine system in normal and unbalanced grid fault modes. Int J Circ Theor App, 2024.[DOI]

[39] Ahmed M., Harbi I., Kennel R., Abdelrahem M. Direct Power Control Based on Dead-beat Function and Extended Kalman Filter for PV Systems. in Journal of Modern Power Systems and Clean Energy, 2023; 11: 863-872.[DOI]

[40] Huang J, Zhang A, Zhang H et al. Improved Direct Power Control for Rectifier Based on Fuzzy Sliding Mode. IEEE T ContrSyst T, 2014; 22: 1174-1180.[DOI]

[41] Ullah W, Khan F, Hussain S et al. A Novel Dual Port Dual Rotor Wound Field Flux Switching Generator With Uniform and Non-Uniform Rotor Poles for Counter-Rotating Wind Power Generation. IEEE Trans Energ Conver, 2023; 38: 2420-2433.[DOI]

[42] Beik O, Al-Adsani AS. Active and Passive Control of a Dual Rotor Wind Turbine Generator for DC Grids. IEEE Access, 2021, 9: 1987-1995.[DOI]

[43] Ullah W, Khan F, Hussain S. A Novel Dual Rotor Permanent Magnet Flux Switching Generator for Counter Rotating Wind Turbine Applications. IEEE Access, 2022; 10: 16456-16467.[DOI]

[44] Ullah W, Khan F, Hussain S. A Comparative Study of Dual Stator With Novel Dual Rotor Permanent Magnet Flux Switching Generator for Counter Rotating Wind Turbine Applications. IEEE Access, 2022, 10: 8243-8261.[DOI]

[45] Kadi S, Imarazene K, Berkouk EM et al. A direct vector control based on modified SMC theory to control the double-powered induction generator-based variable-speed contra-rotating wind turbine systems. Energ Rep, 2022; 8: 15057–15066.[DOI]

[46] Ullah W, Khan F, Akuru UB et al. A Novel Dual Electrical and Dual Mechanical Wound Field Flux Switching Generator for Co-Rotating and Counter-Rotating Wind Turbine Applications. IEEE T Ind Appl, 2023;60: 184-195.[DOI]

[47] Ullah W, Khan F, Akuru UB et al. Evaluation of Counter-Rotating Dual-Rotor Permanent-Magnet Flux-Switching Machine with Series and Parallel Stator Teeth. Machines, 2023; 11:989.[DOI]

[48] Benbouhenni H, Zellouma D, Bizon N et al. A new PI(1 +PI) controller to mitigate power ripples of a variable-speed dual-rotor wind power system using direct power control. Energ Rep, 2023; 10: 3580-3598.[DOI]

[49] Benbouhenni H, Bounadja E, Gasmi H et al. A new PD(1+PI) direct power controller for the variable-speed multi-rotor wind power system driven doubly-fed asynchronous generator. Energ Rep, 2022; 8: 15584-15594.[DOI]

[50] Zellouma D, et al. Field-oriented control based on parallel proportional–integral controllers of induction motor drive. Energ Rep, 2023; 9: 4846-4860.[DOI]

[51] Taoussi M, Bossoufi B, Bouderbala Met al. Implementation and Validation of Hybrid Control for a DFIG Wind Turbine Using an FPGA Controller Board. Electronics, 2021; 10: 3154.[DOI]

[52] Boudjema Z, Taleb R, Djerriri Y et al. A novel direct torque control using second order continuous sliding mode of a doubly fed induction generator for a wind energy conversion system. Turk J Electr EngCo, 2017; 25: 965-975.[DOI]

[53] Quan Y, Hang L, He Y et al. Multi-Resonant-Based Sliding Mode Control of DFIG-Based Wind System under Unbalanced and Harmonic Network Conditions. Appl Sci, 2019, 9: 1124.[DOI]

[54] Said M, Derouich A, El Ouanjli N et al. Enhancement of the Direct Torque Control by using Artificial Neuron Network for a Doubly Fed Induction Motor. Intel Sys Appl, 2022; 13: 1-18.[DOI]

[55] Tavakoli SM, Pourmina MA, Zolghadri MR. Comparison between different DPC methods applied to DFIG wind turbines. Int JRenew Energy R, 2013; 3: 446-452.

[56] Sahria Y, Tamalouzt S, Hamoudi Fet al. New intelligent direct power control of DFIG-based wind conversion system by using machine learning under variations of all operating and compensation modes. Energ Rep, 2021; 7: 6394-6412.[DOI]

[57] Mahfoud S, Derouich A, Iqbal A et al. Ant-Colony optimization-direct torque control for a doubly fed induction motor: An experimental validation. Energy Reports, 2022; 8: 81-98.[DOI]

[58] Najib E, Aziz D, Abdelaziz E et al. Direct torque control of doubly fed induction motor using three-level NPC inverter. Prot Contr Mod Pow, 2019; 17: 1-9.[DOI]

[59] Amrane F, Chaiba A, BadrEddine B et al. Design and implementation of high performance field oriented control for grid-connected doubly fed induction generator via hysteresis rotor current controller. Rev Roum Sci Tech-Electrotechn Et Energ, 2016; 61: 319-324.

[60] Yaichi I, Semmah A, Wira P et al. Super-twisting sliding mode control of a doubly-fed induction generator based on the SVM strategy. Period Polytech ElectrEng Co, 2019; 63: 178-190.[DOI]

[61] Boudjema Z, Hemici B, Yahdou A. Second order sliding mode control of a dual-rotor wind turbine system by employing a matrix converter. J Electr Eng, 2016; 16: 11-11.

[62] Ayrira W, Ourahoua M, Hassounia BE et al. Direct torque control improvement of a variable speed DFIG based on a fuzzy inference system. MathComput Simulat, 2020; 167: 308-324.[DOI].

[63] Bouderbala M, Bossoufi B, Deblecker O et al. Experimental Validation of Predictive Current Control for DFIG: FPGA Implementation. Electronics, 2021; 10: 2670.[DOI]

[64] Benbouhenni H, Ilhami C, Nicu B et al. Direct Vector Control Using Feedback PI Controllers of a DPAG Supplied by a Two-Level PWM Inverter for a Multi-rotor Wind Turbine System. Arab J Sci Eng, 2023; 48:15177-15193.[DOI]

[65] Ravikiran H, Tukaram M. Modified super twisting algorithm based sliding mode control for LVRT enhancement of DFIG driven wind system. Energ Rep, 2022; 8:3600–3613.[DOI]

[66] Xiahou K, Li MS, Liu Y et al. Sensor fault tolerance enhancement of DFIG-WTs via Perturbation Ob-server-Based DPC and Two-Stage Kalman Filters. IEEE Trans Energ Conver, 2018; 33: 483-495.[DOI]

[67] Farah N, Talib MHN, Shah NSM et al. A Novel Self-Tuning Fuzzy Logic Controller Based Induction Motor Drive System: An Experimental Approach. in IEEE Access, 2019; 7: 68172-68184.[DOI]

 

Copyright © 2024 The Author(s). This open-access article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, sharing, adaptation, distribution, and reproduction in any medium, provided the original work is properly cited.

 

Brief of Corresponding Author(s)

Habib Benbouhenni He is currently Professor with the University of Nisantasi, Turkey. He is a PhD in the Departement of Electrical Engineering at the ENPO-MA, Oran, Algeria. He received an M.A. degree in automatic and informatique industrial in 2017. He is editor of seven books and more than 150 papers in scientific fields related to electrical engineering. His research activities include the application of robust control in wind turbine power systems. The h-index value in Google is 28 at the moment.