Phonopy Calculations of Thermodynamic Properties and Phase Transitions of CsSnI₃ Based on SCAN-relaxed Structures

 

Dilshod Nematov1, Amondulloi Burhonzoda1*, Kholmirzo Kholmurodov1,2,3

 

1S.U. Umarov Physical-Technical Institute of the National Academy of Sciences of Tajikistan, Dushanbe, Tajikistan

2Frank Laboratory of Neutron Physics, Joint Institute for Nuclear Research, Dubna, Russia

3Dubna State University, Dubna, Russia

 

*Correspondence to: Amondulloi Burhonzoda, PhD, Senior Researcher, S.U. Umarov Physical-Technical Institute of the National Academy of Sciences of Tajikistan, Dushanbe, 734042, Tajikistan; E-mail: amondullo.burkhonzoda@mail.ru

 

DOI: 10.53964/id.2024017

 

Abstract

In this work, the structural stability of cubic (α), tetragonal (β), and orthorhombic (γ) phases of perovskite CsSnI3 and their phase transitions have been studied by density functional theory (DFT) calculations, and the results obtained have been compared with the characteristics of nonperovskite orthorhombic (δ) modification of CsSnI3 compounds. The relaxed structures of the CsSnI3 phases were produced and their geometrical properties were assessed using the strictly constrained normalized potential (SCAN) functional. According to the results, the energetic hierarchy of CsSnI3 polymorphs is Eβ>Eα>Eγ>Eδ. The phonon and thermodynamic characteristics as well as the temperatures of phase transitions of CsSnI3 have been estimated using the Phonopy tool based on SCAN relaxed structures. The nature of the change in the total energy of the four phases of CsSnI3 from VASP package calculations justifies the trends of free energy, entropy, enthalpy, and heat capacity. In contrast, the β- phase, which has the highest energy among the perovskite phases, is extremely unstable. It was discovered that the tetragonal phase becomes stable at 450K and transitions to the cubic phase at lowering temperatures. CsSnI3 undergoes a phase transition between γ- and β-phases at 300-320K. At temperatures below 320K, a black-yellow transformation of CsSnI3 occurs, in which the black perovskite transforms into a yellow non-perovskite conformation. It was found that temperature phase transitions occur between two orthorhombic phases of CsSnI3 at 360K, although direct transitions of the α⟷γ and γ⟷δ types have not yet been reported in the literature, with the exception of γ→δ transitions under the influence of moisture.

 

Keywords: computer first-principles calculations, density function theory, thermodynamic properties, lead-free perovskites, instability, phase transitions, renewable energy, sustainable development, photovoltaic applications

 

1 INTRODUCTION

Metal halide perovskites have garnered significant interest from a diverse array of researchers and industrial businesses worldwide in recent years. Solar cells, catalysts, light-emitting diodes (LEDs), lasers, X-ray detectors, photodetectors, and field-effect transistors are only a few of the technological and commercial uses for them[1-10]. The development of LEDs and luminous bodies with light pumping in the form of luminescent materials has also made halide perovskites popular and advised[8-10].

 

Perovskite-based semiconductor functional materials have remarkable physical and chemical properties, including tunable energy band gap, low reflectance, a fairly broad absorption spectrum, high absorption coefficient, good photoconductivity, high charge carrier mobility, low exciton binding energy and long diffusion lifetime, optimal electron-hole diffusion lengths, and ferroelectricity[8-13]. These attributes account for the growing demand in this field. They are now widely utilised as the primary raw material in the absorption layers of solar converters and are actively contributing to the global campaign to combat environmental pollution by lowering the proportion of carbon dioxide emissions. Since the massive burning of fossil fuels in recent years has resulted in the release of enormous amounts of greenhouse gases into the atmosphere, such as CO2 and CH4, perovskites, along with other materials, are actively involved in the programme to reduce the rate of use of the earth's depleting fossil fuels in the long run. In order to avert the dire implications of global warming in the near future, authorities in major powers are expressing increasing interest in creating new alternatives to renewable (clean or low-carbon) energy sources in order to cut greenhouse gas emissions and ensure energy independence. Solar energy is the most promising of the various renewable energy sources now available around the world. According to NREL[14], in recent years, the efficiency of perovskite solar cells has increased markedly from 3.8% to more than 26.1%. The highest reported power conversion efficiency ratio for layered lead perovskite (MAPbI3) solar cells is 25.2%[15]. However, these substances exhibit instability in response to temperature, humidity, UV radiation, and other environmental factors[16]. Another notable problem is the relatively low dielectric constant of Pb-containing perovskites (MA, Cs) PbX3 (X = I, Br, Cl and F), as a result of which the rate of charge recombination increases and the performance characteristics of solar cells based on them deteriorate[17]. Lead (Pb), which is poisonous and may be harmful to the environment, is another issue[18]. The development and enhancement of lead-free perovskites’ properties as a substitute for those containing toxic lead is therefore crucial. This supports the EU regulation that prohibits and restricts the use of compounds containing lead (Pb) in all electronic and electrical devices because of its toxicity impact[18], which aligns with the objectives of the UN sustainable development strategy, specifically SDGs 7 and 13[19,20].

 

Lead-free alternative new metal halide organic-inorganic compounds have supplanted lead-containing perovskites in recent years, and materials scientists are working hard to develop these materials. The superior conductivity and absorption of inorganic perovskites made by substituting Sn and Ge for Pb have garnered interest compared to lead-based perovskites. It is asserted, meanwhile, that certain of these chemicals have additional issues. For instance, it was discovered that CsSnBr3 exhibits plasticity while CsGeI3 exhibits brittle behaviour[21,22]. Numerous other candidates exist, such as yellow-phase compounds based on Cs and Sn trihalides (δ-CsSnI3, δ-CsSnBr3, δ-CsSnCl3, and δ-CsSnF3), which lack the aforementioned drawbacks but are characterised by a large band gap that lowers the material's absorption capacity. Controlling the band gap, however, can be achieved easily by temperature-induced phase transitions[23,24], hydrostatic pressure and impurity composition and doping changes[25]. It is known that in addition to the effect of temperature on the phase transition of perovskites, pressure is an important tool for effective control of the phase structure[26-28].

 

CsSnI3 appears to be the most promising of these chemicals. Though the issue of low stability prevents further advancement in this field, black low-bandgap versions of CsSnI3 are well suited for solar systems. Develop a plan for the suitable introduction of external influences, such as the influence of temperature and doping, in order to successfully advance in this direction and improve the properties of CsSnI3. This will allow for the control and optimisation of the band gap in addition to increasing stability. The stability and band gap in any metal halide perovskites of the general formula ABX3 have been shown in recent years to strongly depend on the interaction of “B” and “X” of the group X = I, Br, Cl, and F. These factors increase with increasing electronegativity of the “X” cation, which in turn causes a decrease in the length of the B–X bond[29]. However, it has been demonstrated that substituting an element for the “A” position does not significantly alter the band gap; instead, it mediates the patterns and effects of the B–X interaction through the lattice parameter, which can occasionally occur in conjunction with a phase transition brought on by doping[30]. Furthermore, comprehending the nature of temperature-dependent phase transition influence on the electrical structure and Fermi level behaviour is essential for a thorough investigation of doping-induced phase transitions and their impact on the variation in the band gap of CsSnI3.

 

In recent decades, there has been growing interest in studying the influence of the thermodynamic parameters of perovskites on their electronic and optical properties. This is because the consistent performance of devices based on these materials and their numerous technological applications are closely related to the thermal and thermodynamic properties of the raw materials from which they are made into electronic devices.

 

As a consequence of recent theoretical research on perovskites’ characteristics in addition to experimental observations, perovskite solar cells' efficiency has been steadily rising. Density functional theory (DFT) is one such potent theoretical technique that, in the last ten years, has grown to be a significant tool for the theoretical study of solid materials. This is because DFT offers a highly accurate reformulation of quantum mechanical calculations of solids and accounts for the behaviour of electrons in all atomic-molecular environments. This is because contemporary computing clusters can solve the Kohn-Sham equations efficiently[31]. However, these formulas are predicated on a single estimate, that of the exchange-correlation energy, which accounts for the precision of quantum computations.

 

This work investigates the temperature phase transitions and structural stability of lead-free perovskite based on CsSnI3 through DFT simulations. In order to accurately evaluate the phonon properties and phase transitions of CsSnI3, the structure of the materials under study was well relaxed using the strictly constrained normalized potential (SCAN) functional. This is because an accurate evaluation of the thermodynamic properties is crucial for selecting the right alloying element to stabilise CsSnI3 under environmental conditions.

 

2 METHODS

The structural properties of the α-, β-, γ- and δ-phases of CsSnI3 are investigated based on DFT. Calculations were carried out in the VASP plane wave package[32]. The crystal structures of α-CsSnI3 (cubic), β-CsSnI3 (tetrogonal), γ-CsSnI3 (orthorhombic) and δ-CsSnI3 (non-perovskite orthorhombic) were fully optimized taking into account the relaxation of lattice parameters and atomic positions. All four modifications of CsSnI3 were relaxed using SCAN[33]. However, all SCF calculations were implemented using the generalized gradient approximation to avoid large values of the calculated energy. The electronic states Cs[5s25p66s1], I[5s25p5] and Sn[5s25p2] were considered as valence electrons. A kinetic energy cutoff value of exactly 450eV was established based on the results of the convergence test. Monkhrost-Pack grids of 8×8×8, 6×6×8, 5×5×4, and 5×10×3 were installed for cubic, tetragonal, orthorhombic (perovskite), and orthorhombic (non-perovskite) phases, respectively. However, 800 eV has been established as the cutoff energy value for calculations of thermodynamic properties. The Phonopy code[34] was used to calculate thermodynamic characteristics and phonon dispersion at lower k-point values because these calculations are computationally demanding, particularly for larger systems with low symmetry. Using VASP as a calculator, the forces were computed on supercells of the following sizes: 2×2×2(α), 2×1×2(β), 1×1×2(γ), and 1×2×1(δ). Phonon frequency estimates were selected on an interpolated grid of 32×32×32 q-points (for the α and β phases) and 24×24×24 for the two orthorhombic (γ and δ) phases. The calculations in the Phonopy package are carried out on a 40-atom supercell using a reduced k-point grid (6×6×6, 6×5×5, 3×2×3, and 2×4×2 for α, β, γ, and δ - phases, respectively). As the temperature of phase transitions of CsSnI3 were taken the temperatures in which the difference of calculated free energy of phases (DF) is equal to zero, and the value of F for the α, β, γ and δ phases was considered as the sum of their Helmholtz free energies from Phonopy calculations and the value of free energy (E0) found from VASP calculations:

 

F(T) = U – TS = E0 + ΔU (T) – TS(T)

where ΔU is the difference in internal energies.

 

3 RESULTS AND DISCUSSION

The relaxed geometric characteristics and crystal lattice constants of the α-, β-, γ- and δ- modifications of CsSnI3 are given in Table 1 and compared with the results of experimental measurements.

 

Table 1. Relaxed Lattice Constants of α-, β-, γ- and δ- phases of CsSnI3

 

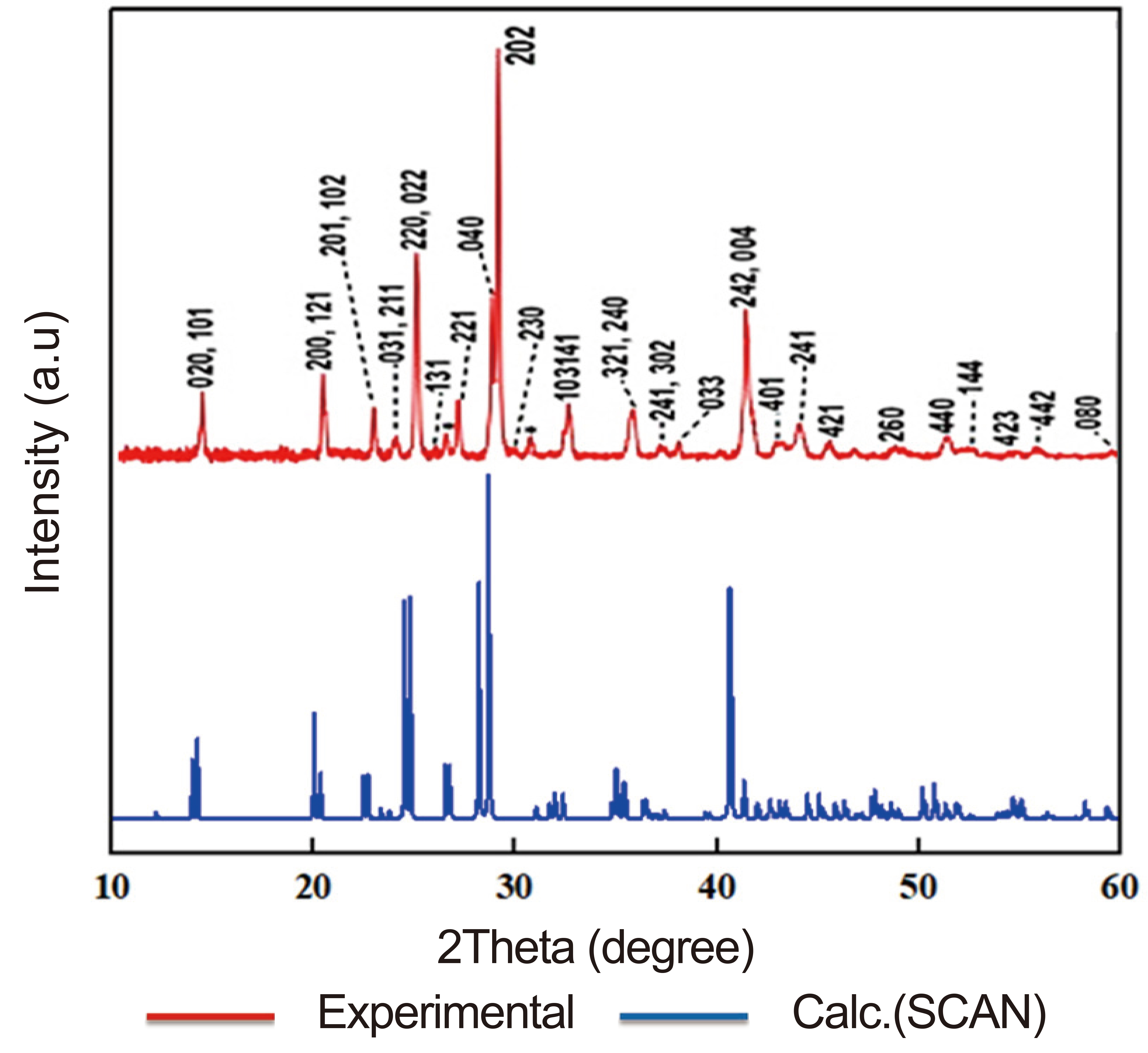
According to Table 1, in contrast to the well-known generalized gradient functional proposed by Perdew-Burke-Ernzerhof, which usually does not very correctly estimate lattice parameters, the SCAN functional will be able to give results comparable and in good agreement with experiment, which indicates its effectiveness for optimizing similar solid-state systems. This agreement is also evident when comparing our calculated X-ray diffraction patterns (using the example of γ-CsSnI3) with the findings of Zhou et al.[36], which makes it evident that our results are similar to those of the experimental observations (Figure 1). Calculations indicate that the phase transformation of CsSnI3 results in a considerable change of interatomic distances, particularly Sn-I. The bond angles Sn-I1-Sn and Sn-I2-Sn likewise alter as a result.

 

Figure 1. Comparison of theoretical X-ray patterns of γ-CsSnI3 with X-ray patterns of the orthorhombic phase of CsSnI3 perovskite[36] obtained by the Bridgman method.

 

The values of total energies of the α-, β-, γ-, and δ-phases of CsSnI3 are compared in Table 2, which indicates that the δ-modification of this compound is the most stable conformation for CsSnI3. γ-CsSnI3, on the other hand, is the most stable iodide with a perovskite structure. Our ground state calculations precisely reproduce the phase stability of CsSnI3 at the ambient temperatures.

 

Table 2. Calculated Total Energies (E) of CsSnI3 Phases

 

The non-porovskite phase of CsSnI3 has the lowest energy structure, based on the results shown in Table 2. That is, at 0K, the most stable phase is the non-perovskite phase (δ-CsSnI3), which is followed by γ-CsSnI3.

 

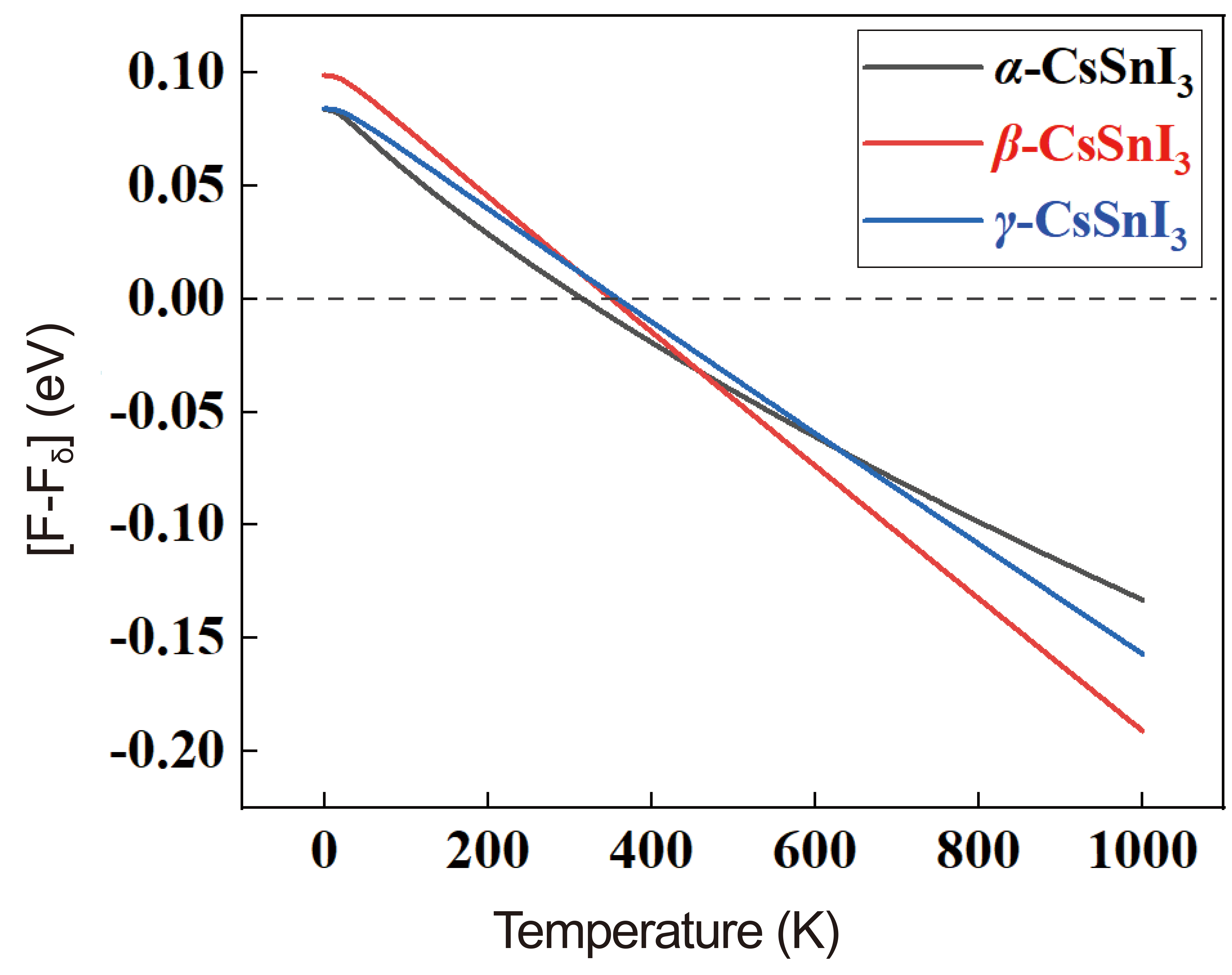
In addition to the results presented in Table 2, we obtained temperature-dependent curves of Helmholtz free energy and relative entropy, as well as phonon modes from which we can evaluate the correctness of the field energy-based stability assessment approach[37]. In Figure 2 shows graphs of the temperature dependence of the Helmholtz free energy (F) for the α-, β-, γ-phases relative to the δ-phase of CsSnI3. Also in Figure 3A and B shows the temperature dependence curves of entropy (ΔS) and heat capacity (Cv) for four phases of CsSnI3.

 

Figure 2. Free energy difference (Helmholtz) of the α-, β-, γ-phase relative to the δ-modification of CsSnI3 as a function of absolute temperature.

 

According to the results of Figure 2, at 0K, the β phase has the highest energy among the perovskite phases, and the energy value for the γ phase is the lowest. In this case, the cubic phase is fixed between these phases. However, according to the graph, it is the tetragonal phase that becomes the most stable at high temperatures. The orthorhombic perovskite phase remains energetically close to the α phase up to high temperatures. The results of calculations indicate that in the 320-360K range, there is energy rivalry between the β- and γ-phases of CsSnI3 and its non-perovskite phase. The free energy of high-temperature phases in nearly all temperature ranges is higher than the free energy δ-CsSnI3, which defies the direct dependence of free energy and material stability, as shown by the data in Figure 3. A similar tendency can also be seen in the overall heat capacity image.

 

Figure 3. Variation of the entropy (A) and heat capacity (B) depending on temperature for α-, β-, γ- and δ-phases of CsSnI3.

 

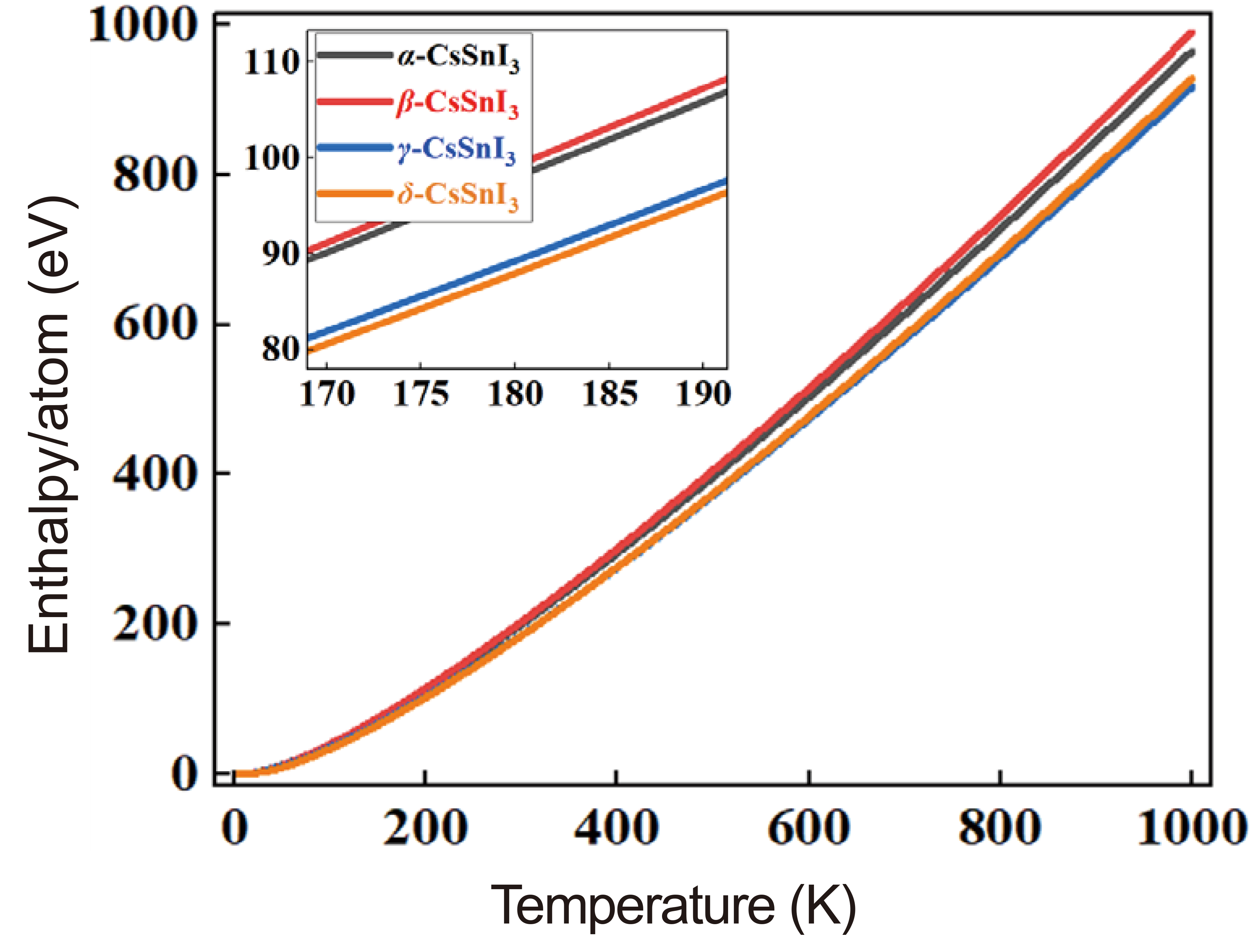
Figure 4 compares and shows the enthalpy dependence curves (ΔH) of the systems under study, obtained based on the expression:

ΔH=F+ΔS*T

where T is the absolute temperature. From the results, it can be seen that the β phase has the highest enthalpy and the δ phase is naturally the lowest in all temperature ranges.

 

Figure 4. Temperature-dependent enthalpy vibration of α-, β-, γ- and δ-phases of CsSnI3.

 

The phase transition temperatures for CsSnI3 were then determined by subtracting the estimated free energies of the phases ([α-β], [β-γ], and [α-δ]). In this case, the free energy was calculated as the sum of the minimum energy obtained from the VASP calculations with the Helmholtz free energies from the calculated Phonopy package. Phase transition diagrams were plotted in independent coordinate systems and further combined into one figure (Figure 5) to compare phase transition diagrams in the same range of energy differences, since CsSnI3 phases undergo complex phase transitions at different temperatures.

 

Figure 5. Comparison of the temperature dependence of the free energy difference at phase transitions of CsSnI3 (A), and separate diagrams of the temperature dependence of phase transformations such as α⟷β (B), β⟷γ (C), and α⟷δ (D) for CsSnI3..

 

According to the results presented in Figure 5, CsSnI3 crystals are characterized by three cases of phase transitions in certain temperature ranges. The critical temperature points of the phase transitions α⟷β, β⟷γ and α⟷δ indicate that the stability regions of these phases differ significantly from each other (Figure 5A). At temperatures above 450K, the tetragonal phase becomes stable, and below this temperature it transforms into the cubic phase (Figure 5B). The phase transition between the tetragonal and orthorhombic modifications occurs in the range of 300-320K (Figure 5C). At 320K, there is a transformation between the CsSnI3 perovskite structure and its non-perovskite analogue, which is known as the black-yellow transformation (Figure 5D). The results obtained are similar to the experimental measurements of Yamada et al.[38] with the exception of the temperature of phase transitions between the α and δ phases of the perovskite. Calculations have also shown the presence of temperature phase transitions between two orthorhombic phases of CsSnI3 at 360K, although direct transitions of the α⟷γ and γ⟷δ types have not yet been reported in the literature, with the exception of γ→δ transitions under the influence of moisture[39]. The relative stability of the non-perovskite phase of CsSnI3 is indicated by the lack of negative frequencies in Figure 6, which displays the results of first-principles calculations of the density of phonon states.

 

Figure 6. Phonon state densities for: α-CsSnI3 (A), β-CsSnI3 (B), γ-CsSnI3 (C) and δ-CsSnI3 (D).

 

According to calculations, the tetragonal phase has a moderate contribution from the phonon state (Figure 6B) than its orthorhombic (Figure 6C) and cubic modifications (Figure 6A). The results obtained can be used by experimentalists for further research of crystals and thin films based on CsSnI3, and also complement the data bank of research conducted in the field of using perovskites to generate green energy[40-50].

 

4 CONCLUSION

Using DFT calculations, issues of the structural stability of CsSnI3 compounds are considered. Relaxed structures for four phases of CsSnI3 were obtained and their structural stability was assessed from the point of view of comparing the total energy, entropy and enthalpy of their formation. The trends in free energy, entropy, enthalpy, heat of formation and heat capacity are justified in terms of the pattern of changes in the total energy of the four phases of CsSnI3 from VASP calculations. Stable phases of CsSnI3 at 0K are shown and compared. The critical temperatures of phase transitions are found, including the temperature of the black-yellow transformation of CsSnI3. The presence of temperature phase transitions between two orthorhombic phases of CsSnI3 at 360K was discovered, despite the fact that direct transitions of the α⟷γ and γ⟷δ types have not yet been reported in any experiment, with the exception of the γ→δ transitions under the influence of moisture. This study will help to deeply understand the features of the thermodynamic properties of CsSnI3 and list the disadvantages of their properties, so that in the future it is advisable to take measures and select stabilizing elements, without gross negative impact on their optoelectronic properties, including the band gap and the ability of good photoabsorption.

 

Acknowledgements

The work was performed at the S.U. Umarov Physical-Technical Institute of the National Academy of Sciences of Tajikistan with the support of International Science and Technology Center (ISTC), project TJ-2726.

 

Conflicts of Interest

The authors declared no conflict of interest.

 

Author Contribution

The work submitted for publication is a joint work of the authors. Nematov D formulated the concept of quantum-chemical solution of the problem with Kholmurodov K, and the analysis of data was directly carried out by Burhonzoda A.

 

Abbreviation List

DFT, Density functional theory

LEDs, Light-emitting diodes

SCAN, Strictly constrained normalized potential

 

References

[1] Xiao Z, Kerner RA, Zhao L et al. Efficient perovskite light-emitting diodes featuring nanometresized crystallites. Nat Photonics, 2017; 11: 108-115.[DOI]

[2] Lanzani G, Petrozza A, Caironi M. Organics go hybrid. Nat Photonics, 2017; 11: 20-22.[DOI]

[3] Hwang J, Rao RR, Giordano L et al. Perovskites in catalysis and electrocatalysis. Science, 2017; 358: 751-756.[DOI]

[4] Kim YC, Kim KH, Son DY et al. Printable organometallic perovskite enables large-area, low-dose X-ray imaging. Nature, 2017; 550: 87-91.[DOI]

[5] Akyüz Ö, Scheffner M, Cölfen H. Fluorescent Cadmium Chalcogenide Nanoclusters in Ubiquitin. Small Struct, 2021; 2: 2170004.[DOI]

[6] Shahrokhi S, Gao W, Wang Y et al. Emergence of ferroelectricity in halide perovskites. Small Methods, 2020; 4: 2000149.[DOI]

[7] Bakr OM, Mohammed OF. Powering up perovskite photoresponse. Science, 2017; 355: 1260-1261.[DOI]

[8] Chen J, Zhou S, Jin S et al. Crystal organometal halide perovskites with promising optoelectronic applications. J Mater Chem C, 2016; 4: 11-27.[DOI]

[9] Sutherland BR, Hoogland S, Adachi MM et al. Conformal Organohalide Perovskites Enable Lasing on Spherical Resonators. ACS Nano, 2014; 8: 10947-10952.[DOI]

[10] Zhu H, Fu Y, Meng F et al. Lead halide perovskite nanowire lasers with low lasing thresholds and high-quality factors. Nat Mater, 2015; 14: 636-642.[DOI]

[11] Zhang Z, Ghimire S, Okamoto T et al. Mechano-optical Modulation of Excitons and Carrier Recombination in Self-Assembled Halide Perovskite Quantum Dots. ACS Nano, 2022; 16: 160-168.[DOI]

[12] Yin WJ, Shi T, Yan Y. Unique properties of halide perovskites as possible origins of the superior solar cell performance. Adv Mater, 2014; 26: 4653-4658.[DOI]

[13] Kovalenko MV, Protesescu L, Bodnarchuk MI. Properties and potential optoelectronic applications of lead halide perovskite nanocrystals. Science, 2017; 358: 745-750.[DOI]

[14] National Renewable Energy Laboratory. Best Research-Cell Efficiency Chart. Accessed in May 3, 2024. Available at:[Web]

[15] Yang WS, Park BW, Jung EH et al. Iodide management in formamidinium-lead-halide-based perovskite layers for efficient solar cells. Science, 2017; 356: 1376-1379.[DOI]

[16] Correa-Baena JP, Saliba M, Buonassisi T et al. Promises and challenges of perovskite solar cells. Science, 2017; 358: 739-744.[DOI]

[17] Sun PP, Li QS, Yang LN et al. Theoretical insights into a potential lead-free hybrid perovskite: substituting Pb2+ with Ge2+. Nanoscale, 2016; 8: 1503-1512.[DOI]

[18] Lira-Cantú M. Perovskite solar cells: Stability lies at interfaces. Nat Energy, 2017; 2: 17115.[DOI]

[19] UNDP. Goal 7: Affordable and clean energy. Accessed in May 18, 2024 Available at:[Web]

[20] UNDP. Goal 13: Climate action. Accessed in May 18, 2024. Available at:[Web]

[21] Roknuzzaman M, Ostrikov K, Wang H et al. Towards lead-free perovskite photovoltaics and optoelectronics by ab-initio simulations. Sci Rep, 2017; 7: 14025.[DOI]

[22] Brik MG. Comparative first-principles calculations of electronic, optical and elastic anisotropy properties of CsXBr3 (X = Ca, Ge, Sn) crystals. Solid State Commun, 2011; 151: 1733-1738.[DOI]

[23] Grote C, Berger RF. Strain tuning of tin-halide and lead-halide perovskites: a first-principles atomic and electronic structure study. J Phys Chem C, 2015; 119: 22832-22837.[DOI]

[24] Knutson JL, Martin JD, Mitzi DB. Tuning the band gap in hybrid tin iodide perovskite semiconductors using structural templating. Inorg Chem, 2015; 44: 4699-4705.[DOI]

[25] Akkerman QA, D'Innocenzo V, Accornero S et al. Tuning the optical properties of cesium lead halide perovskite nanocrystals by anion exchange reactions. J Am Chem Soc, 2015; 137: 10276-10281.[DOI]

[26] Huang Y, Yin WJ, He Y. Intrinsic point defects in inorganic cesium lead iodide perovskite CsPbI3. J Phys Chem C, 2018; 122: 1345-1350.[DOI]

[27] Cao Y, Qi G, Sui L. Pressure-induced emission enhancements of Mn2+-doped cesium lead chloride perovskite nanocrystals. ACS Mater Lett, 2020; 2: 381-388.[DOI]

[28] Ma Z, Xiao G, Zou B. Step forward to light up the future: pressure-induced emission. Sci Bull, 2023; 68: 1588-1590.[DOI]

[29] Metin DZ, Nicola G. Internal and external pressure in cubic perovskites: electronic structure effects and systematic accuracy from first principles. Electron Struct, 2019; 1: 035001.[DOI]

[30] Yin WJ, Yang JH, Kang J et al. Halide perovskite materials for solar cells: a theoretical review. J Mater Chem A, 2015; 3: 8926-8942.[DOI]

[31] Banerjee AS, Elliott RS, James RD. A spectral scheme for Kohn-Sham density functional theory of clusters. J Comput Phys, 2015; 287: 226-253.[DOI]

[32] Kresse G, Furthmuller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp Mater Sci, 1996; 6: 15-50.[DOI]

[33] Sun J, Ruzsinszky A, Perdew JP. Strongly constrained and appropriately normed semilocal density functional. Phys Rev Lett, 2015; 115: 036402.[DOI]

[34] Togo A, Chaput L, Tadano T et al. Implementation strategies in phonopy and phono3py. J Phys-Condens Mat, 2023; 35.[DOI]

[35] Chung I, Song JH, Im J et al. CsSnI3: semiconductor or metal? High electrical conductivity and strong near-infrared photoluminescence from a single material. High hole mobility and phase-transitions. J Am Chem Soc, 2012; 134: 8579-8587.[DOI]

[36] Zhou Y, Garces HF, Senturk BS. Room temperature "one-pot" solution synthesis of nanoscale CsSnI3 orthorhombic perovskite thin films and particles. Mater Lett, 2013; 110: 127-129.[DOI]

[37] Togo A, Chaput L, Tanaka I et al. First-principles phonon calculations of thermal expansion in Ti3SiC2, Ti3AlC2, and Ti3GeC2. Phys Rev B, 2010; 81: 174301.[DOI]

[38] Yamada K, Funabiki S, Horimoto H et al. Structural phase transitions of the polymorphs of CsSnI3 by means of rietveld analysis of the X-ray diffraction. Chem Lett, 1991; 20: 801-804.[DOI]

[39] Wang Y, Liu J, Wang J et al. Phase Stability and Transformations in CsSnI3: Is Anharmonicity Negligible? J Phys Chem C, 2022; 126: 19470-19479.[DOI]

[40] Davlatshoevich ND, Islomovich MB, Temurjonovich YM et al. Optimization Optoelectronic Properties ZnxCd1-xTe System for Solar Cell Application: Theoretical and Experimental Study. Biointerface Res App, 2023; 13.[DOI]

[41] Nematov DD, Kholmurodov KT, Yuldasheva DА et al. Ab-initio Study of Structural and Electronic Properties of Perovskite Nanocrystals of the CsSn [Br1− xIx]3 Family. HighTech Innov J, 2022; 3: 140-150.[DOI]

[42] Doroshkevich AS, Nabiev AA, Shylo AV et al. Frequency Modulation of the Raman Spectrum at The Interface DNA-ZrO2 Nanoparticles. Egypt J Chem, 2019; 62: 13-20.[DOI]

[43] Dilshod N, Kholmirzo K, Aliona S et al. On the optical properties of the Cu2ZnSn[S1−xSex]4 system in the IR range. Trends Sci, 2023; 20: 4058-4058.[DOI]

[44] Nematov D, Kholmurodov K. A DFT study of structure, electronic and optical properties of Se-doped kesterite Cu2ZnSnS4 (CZTSSe). Lett Appl Nanobiosci, 2023; 12: 67.[DOI]

[45] Nematov D, Husenzoda M, Burhonzoda A, Kholmurodov K, Lyubchyk A, & Ibrakhim M. Investigation of structural and optoelectronic properties of N-doped hexagonal phases of TiO2 (TiO2-xNx) nanoparticles with DFT realization: Optimization of the band gap and optical properties for visible-light absorption and photovoltaic applications. Bioint Res Appl Chem, 2022; 12: 3836-3848. [DOI]

[46] Luo Y, Li X, Cheng H et al. Ultrahigh thermoelectric performance in RbGe I3/CsSn I3 superlattices. Phys Rev B, 3024; 109: 085305.[DOI]

[47] Nematov DD, Burhonzoda AS, Khusenov MA et al. The quantum-chemistry calculations of electronic structure of boron nitride nanocrystals with density Functional theory realization. Egypt J Chem, 2019; 62: 21-27.[DOI]

[48] Nematov DD, Burhonzoda AS, Kholmurodov KT et al. A Detailed Comparative Analysis of the Structural Stability and Electron-Phonon Properties of ZrO2: Mechanisms of Water Adsorption on t-ZrO2 (101) and t-YSZ (101) Surfaces. Nanomaterials, 2023; 13: 2657.[DOI]

[49] Mohammed MK, Al-Gazally ME., Khaleel OA et al. Improved eco-friendly CsSn0.5Ge0.5I3 perovskite photovoltaic efficiency beyond 20% with SMe-TATPyr hole-transporting layer. Phys Chem Chem Phys, 2024; 26: 3229-3239.[DOI]

[50] Becker WJ, Will G. Röntgen-und Neutronenbeugungsuntersuchungen an Y2Ti2O7. Zeitschrift für Kristallographie-Crystalline Materials, 1970; 131: 278-288.[DOI]

 

Copyright © 2024 The Author(s). This open-access article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, sharing, adaptation, distribution, and reproduction in any medium, provided the original work is properly cited.